Besedilo naloge
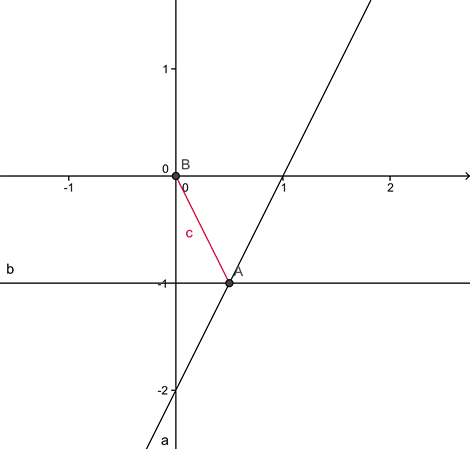
V dani koordinatni sistem narišite premico z enačbo . Na premici narišite točko A z ordinato −1 . Zapišite absciso točke in izračunajte, koliko je točka A oddaljena od izhodišča koordinatnega sistAema. Rezultat naj bo točen.
Postopek reševanja
Postopek reševanja je opisana na filmčku spodaj.