Besedilo naloge
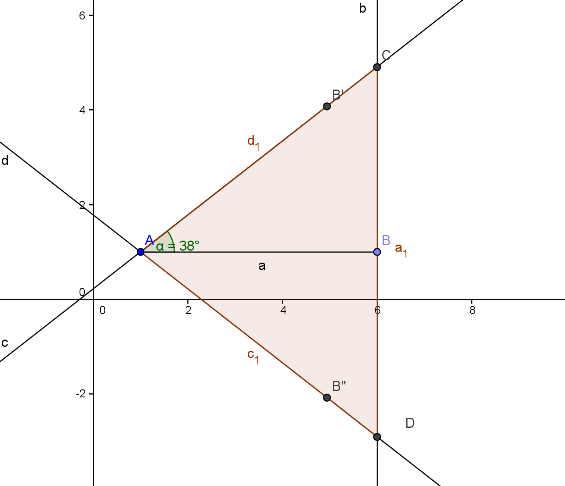
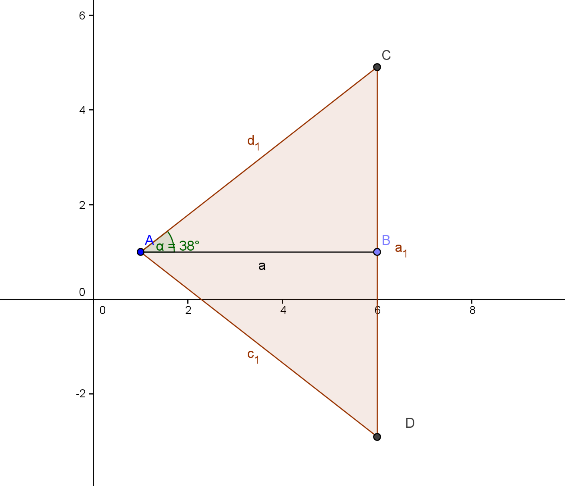
V enakokrakem trikotniku meri višina na osnovnico , kot ob osnovnici pa . Izračunajte dolžini osnovnice in kraka ter ploščino tega trikotnika. Rezultate zaokrožite na 3 mesta.
Postopek reševanja
Postopek reševanja je opisan na filmčku spodaj.