Imamo konkreten matematični problem:

Daljici AB, ki smo jo narisali v GeoGebro poiščimo točko T, ki deli daljico v razmerju 7:3. Rešitev problema bom poiskala na dva različna načina.

1.Način:

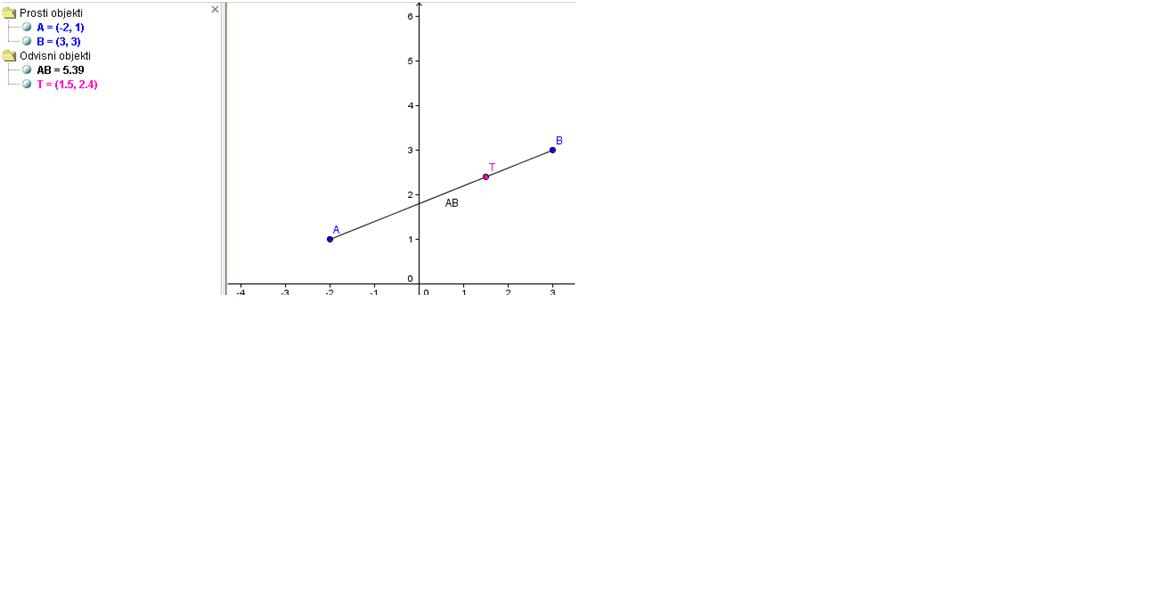
• Izberem si poljubni dve točki, katerih koordinate zapišem v vnosno vrstico. To sta točki A(-2,1)in B(3,3).

• Želim narisati daljico AB. To naredim tako da v vnosno vrstico napišem naslednje: AB= Daljica[A,B].

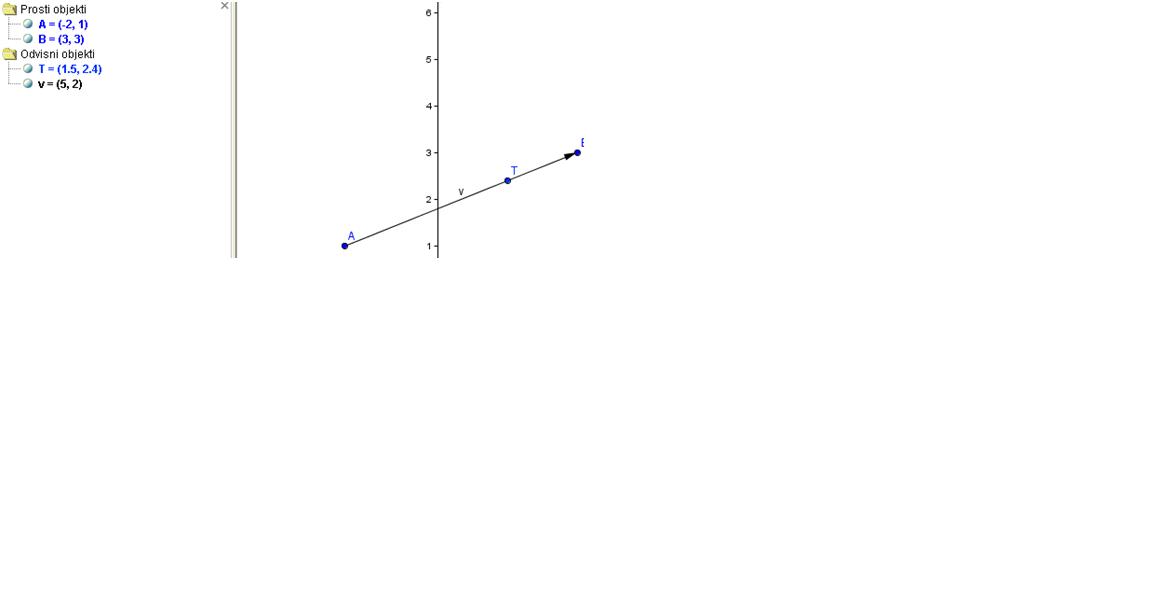
• Narisano imam daljico AB, sedaj pa me zanima, kje se nahaja točka T, ki razdeli daljico AB v razmerju 7:3. Da dobim to točko, v vnosno vrstico napišem T= A+ 7/10 (B-A)

  

2.Način:

• Izberem si poljubni dve točki, katerih koordinate zapišem v vnosno vrstico. To sta točki A(-2,1)in B(3,3).

• Sedaj pa namesto daljice AB, narišemo vektor, ki ima začetno točko v točki A. Vektor sem narisala tako, da sem v vnosno vrstico napisala naslednje: v = Vektor[A, B]

• Ponovno me zanima, kje se nahaja točka T, ki vektor razdeli v razmerju 7:3. Točko T dobim tako, da v vnosno vrstico napišem naslednje: T = A + 7/10 v

Iz prvega primera sem vzela koordinati točk A in B. Kot je razvidno iz spodnje slike ima točka T enake koordinate kot v zgornji sliki. Naloga je rešena pravilno po obeh postopkih.

OBJAVA NA Wiki-ju:

• http://penelope.fmf.unilj.si/jjf/index.php/Wiki_ROM/Zapiski/Geogebra/FAQ_GeoGebra/FAQ_GeoGebra_38