Besedilo naloge
Tangeta na graf funkcije v točki z absciso je pravokotna na premico z enačbo . Izračunajte realno število a.
Posotopek reševanja
Postopek kako rešimo to nalogo, je opisan na filmčku spodaj.
Besedilo naloge in postopek reševanja
Besedilo naloge
Tangeta na graf funkcije v točki z absciso je pravokotna na premico z enačbo . Izračunajte realno število a.
Posotopek reševanja
Postopek kako rešimo to nalogo, je opisan na filmčku spodaj.
Matematično ozadje
Tangenta na graf funkcije f(x) v točki z absciso je premica, ki je pravokotna na prmico . Premici, ki sta pravokotni pa imata nasprotno obratni smerni koeficient se pravi pri premici y je smerni koeficient enak , torej ima tangenta smerni koeficient enak . Odvod funkcije f(x) je . Na primer: ko ugotavljamo kje ima neka funkcija ekstreme, moramo ugotoviti kje je prvi odvod enak 0. V našem primeru pa pogledamo kdaj je ta odvod enak . Ugotovimo, da je pri . Če sedaj vstavimo v funkcij f(x) vredost , izgleda funkcija . Sedaj je tangenta te funkcije v točki z absciso pravokotna na premico .
Konstrukcijski koraki v Geogebri
Po vrsti rišemo / ustvarimo:
Na koncu sem funkcijo f(x) in y obarvala z modro, tangento z rdečo in premico e z zeleno barvo.
Na sliki spodaj sta narisani funkciji f(x) in y, tangenta in premica x=1.
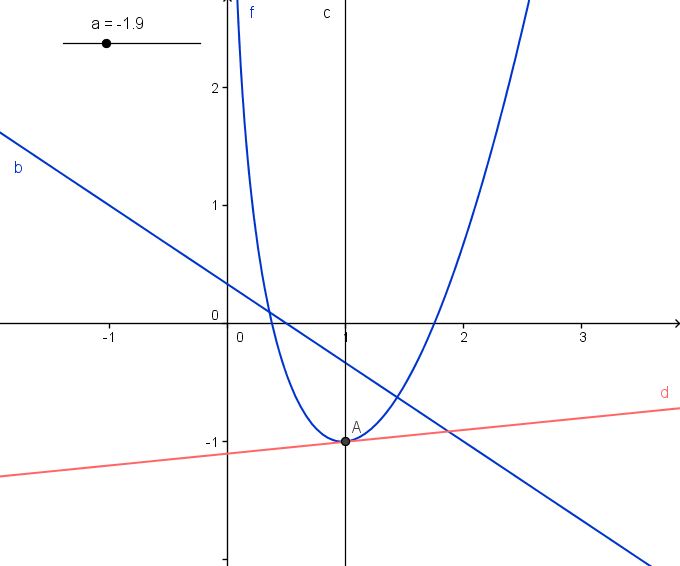
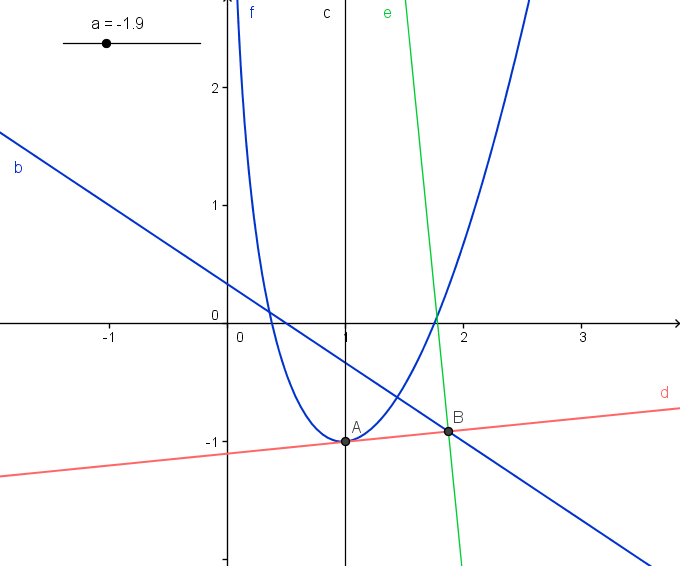
Slika spodaj prikazuje končano konstrukcijo.
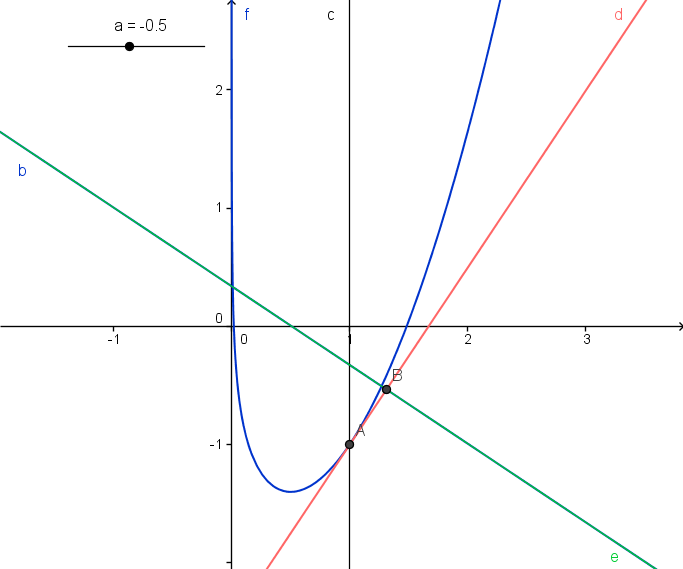
Ko nastavimo vrednost drsnika a na -0.5, se premici b in e prkirjeta. Tedaj sta tudi premica b in tangenta d pravokotni.
Razlaga konstrukcije
Uporaba / rešitev
Ko bomo spreminjali vrednost na drsniku a, se bo spreminjala funkcije f(x), posledično tudi tangenta, prav tako pa tutdi premica e. Pri neki vrednosti na drsniku a, bo ta premica e prekirla premico y. Ker sta tangenta in premica e pravokotni, bo tudi premica y pravokotna na tangento. Ta vrednost na drsniku a, je iskana vrednost. V našem primeru sta si premica in tangenta pravokotni natanko tedaj, ko ima a vrednost -0.5.