Besedilo naloge
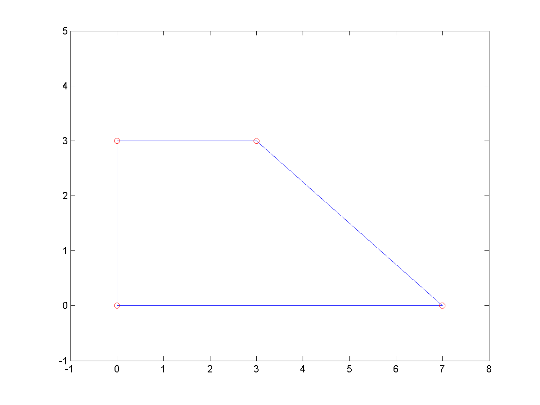
Točke A=(0, 0) , B=(7, 0) , C=(3, 3) in D=(0, 3) so oglišča trapeza. Narišite ga v dani koordinatni sistem. Izračunajte dolžino stranice b = |BC| , skalarni produkt (|AB| ) • (|AC|) in velikost kota ß (ABC) . Dolžino stranice in skalarni produkt izračunajte natančno, kot ß pa zapišite zaokroženo na minute.
Postopek reševanja
Postopek reševanja je opisan na filmčku spodaj.