Določite kot pod katerim se sekata krivulji in .

Kot med krivuljama je kot med tangentama na krivulji v presečišču: , , , kjer sta in smerna koeficienta funkcij.

Opazimo, da je druga enačba že zapisana v predpisanem formatu . Prvo pa moramo še preoblikovati:

• … preuredimo tako, da imamo samo y na levi strani
• … pomnožimo z -1
• … korenimo

Najprej moramo poiskati točko v kateri se ti dve funkciji sekata. To storimo tako da ju enačimo:

• … kvadriramo
• … pomnožimo z 2
• … damo vse na eno stran enačaja

Dobimo rešitvi: in . Ker vemo, da je koren definiran samo za pozitivna števila je možna rešitev ena sama in to je . Tako dobljeno rešitev vstavimo še v eno od podanih enačb in dobimo, da je .

Da bomo lahko izračunali smerni koeficient tangente na krivulji v dobljenem presečišču, moramo obe enačbi odvajati in vanjo vstaviti x koordinato presečišča:

Smerna koeficienta nato vstavim v enačbo in izračunam .

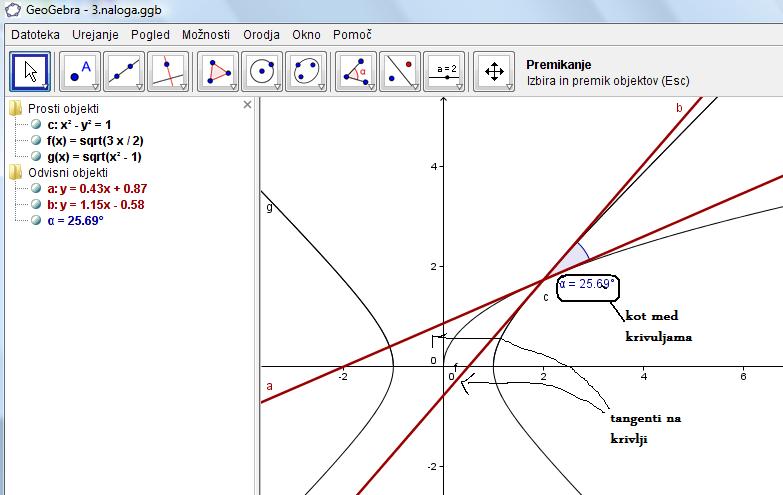
Skico naloge lahko naredimo s pomočjo GeoGebre. To storimo tako, da najprej narišemo krivulji, pri čemer pazimo, da hiperbolo narišemo samo nad ordinatno osjo. Nato skozi njuno presečišče narišemo tangenti na krivulji in izračunamo kot med tangentama.