Izračunajte in klasificirajte lokalne ekstreme funkcije
.

Najprej poiščemo stacionarne točke naše funkcije. To storimo tako, da funkcijo odvajamo in izračunamo za katere x je naša funkcija enaka 0. Pri računanju odvoda si pomagamo s programom TI-Nspire CAS Student Software.

Prvo rešitev opazimo takoj: x = 0, za iskanje druge rešitve pa lahko uporabimo ukaz Solve() v našem programu. Dobimo x =

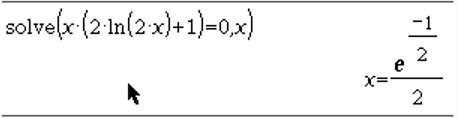
Ker pa 0 ni v definicijskem območju naše funkcije, ta rešitev odpade. Tako je naša stacionarna točka samo x. To pa je hkrati tudi kandidat za lokalni ekstrem. Potrebno je izračunati še drugi odvod funkcije.

Sedaj moramo izračunati še vrednost drugega odvoda v naši stacionarni točki.

f(x) = 2*ln() + 3 = 2*() + 3 = 2

Ker je 2 > 0, pomeni, da ima funkcija f(x) v točki x lokalni minimum.

Narišimo še našo funkcijo v Geogebri. Ustvarimo drsnik b, s pomočjo katerega bomo premikali točko A na funkciji. V ukazno polje napišemo A = (b, f(b)) in tako ustvarimo to točko. Skozi to točko narišimo tangento na funkcijo. Minimum bomo dosegli takrat, ko bo koeficient tangente enak 0. Ker je to z appletom težko doseči, poizkusimo za b določiti takšno vrednost, da bo koeficient tangente enak 0 (vpisujemo vrednosti, za katere ima tangenta na eni strani negativen in na drugi strani pozitiven predznak). Opazimo, da se to zgodi pri 0,303. Primerjamo z izračunanim x.