Naštejmo nekaj izrazov, ki jih bomo potrebovali v nadaljevanju:

Vozlišče: element drevesa, ki ima podatek(-tke) in informacijo o iz njega izhajajočih poddrevesih.

Drevo: je končna množica vozlišč. od katerih je eno posebej označeno kot koren, ostala pa razpadejo na disjunktnih množic , ki imajo tudi lastnosti drevesa. imenujemo poddrevesa. Drevo opiše povezavo vozlišč, izbira podatkov, ki jih vstavimo v vozlišča pa je odvisna od primera uporabe. Narišemo ga od korena v globino.

Poddrevo: je drevo, ki izhaja iz nekega vozlišča.

Velikost drevesa: je število vozlišč v drevesu.

Globina drevesa: je število nivojev med korenom in listom.

Starš: predhodnik vozlišča.

Otrok (ali naslednik): koren poddrevesa nekega vozlišča.

Stopnja vozlišča: število njegovih otrok.

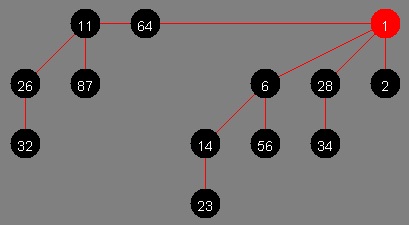
Dvojiško drevo: množica vozlišč, ki je ali prazna ali pa sestoji iz korena in dveh disjunktnih poddreves, levega in desnega. Stopnja drevesa je dva. Ločimo med levim in desnim poddrevesom. Dvojiško drevo je urejeno drevo.

Kopica: levo poravnano dvojiško drevo, pri katerem ključ starša ni manjša oz. večja od vrednosti v otrocih.

Binomsko drevo: je rekurzivna podatkovna struktura, za katero velja:

• koren je najmanjši element v drevesu (urejenost),
• posamezen element je binomsko drevo ,
• binomsko drevo sestoji iz dveh poddreves , pri katerih velja:
  
• manjši od korenov poddreves tudi koren celotnega drevesa in poddrevo z večjim korenom prvi naslednik celotnega drevesa .
  
• binomsko drevo ima lahko poljubno število sinov, vendar je tu kazalec le na skrajno levega sina, ta pa kaže na desne brate.
  

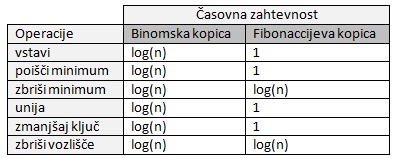
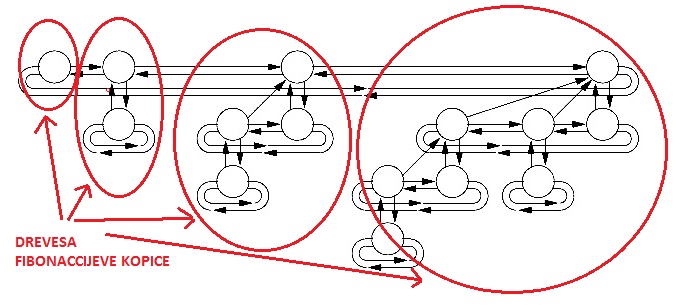
Binomska kopica: je podatkovna struktura. Sestavljena je iz binomskih dreves, ki imajo naslednje lastnosti:

• Vsako binomsko drevo v binomski kopici ima lastnost minimalnih kopic. Ključ vsakega vozlišča mora biti vedno večji ali enak ključu svojega starša. Od tod sledi, da ima koren najmanjši ključ v binomskem drevesu.
• Za vsako nenegativno število k, obstaja samo eno binomsko drevo v kopici, katerega koren ima stopnjo k. Torej binomska kopica ima lahko le 0 ali 1 binomsko drevo s stopnjo k. Ta lastnost pove, da je binomska kopica z n vozlišči sestavljena iz največ binomskih dreves. Več o binomski kopici lahko najdete na: http://www.nauk.si/materials/4992/out/index.html#state=1

Zelo preprosto povedano je to binomska kopica z amortiziranimi operacijami. Torej, so določene operacije manj časovno zahtevne. Je primer posebne oblike dreves, namenjene hitremu iskanju najmanjšega ključa v tej podatkovni strukturi.

Časovna zahtevnost kopic

• Razvila sta jo računalniška znanstvenika Michael Lawrence Fredman in Robert Endre Tarjan leta 1984, prvič pa sta jo objavila leta 1987. S Fibonaccijevo kopico sta izboljšala amortiziran izvajalni čas operacij na binomskih kopicah.

• Ime je dobila po Fibonaccijevem zaporedju, ki se uporablja pri analizi časovne zahtevnosti operacij, torej analizi časa izvajanja operacij.

Fibonaccijeva kopica

OPOMBA: Vse kopice so Fibonaccijeve kopice, drevesa in poddrevesa pa so načeloma lahko precej poljubna, saj oblike Fibonaccijeve kopice ne popravljamo na vsakem koraku in pri vsaki operaciji.

Fibonaccijeva kopica

• Fibonaccijeva kopica je podatkovna struktura, ki zadošča pogoju minimalne kopice. Torej je ključ otroka vedno manjši ali enak podatku očeta. Posledično to pomeni, da se minimalni ključ nahaja v korenu drevesa.

  • ključ(oče)<=ključ(sin)

• Binomska kopica ima obliko binomskega drevesa, vendar potrebujemo pri Fibonaccijevi kopici večjo fleksibilnost oblike. Kopica nima nobene strogo predpisane oblike in v splošnem se lahko vsa vozlišča nahajajo v korenu.

opis slike

Pomembno je razumeti, kako so vozlišča med seboj povezana. V korenu so vsa dvosmerno povezana v cikel. Oče vsebuje kazalec na enega od otrok, ki so tudi dvosmerno povezana v cikel. Vsak otrok vsebuje kazalec, ki kaže na njegovega očeta. Fibonaccijeva kopica vsebuje tudi kazalec, ki kaže na vozlišče z najmanjšim ključem. Koren Fibonaccijeve kopice so vsa vozlišča na 0-tem nivoju (torej vsi bratje vozlišča, ki ima minimalni ključ). Uporablja se za predstavitev vrste s prednostjo. Z njeno uporabo želimo minimizirati število operacij pri iskanju najkrajše poti v grafu in najcenejšega vpetega drevesa v grafu.

• Poleg kazalcev vsako vozlišče vsebuje še ključ, stopnjo vozlišča in bit, ki ga uporabimo za označevanje. Bit za označevanje uporabimo zato, da cela kopica ni pregloboka. Pri nekaterih operacijah označena vozlišča zato premestimo v koren.

• Je lena struktura, ker ne rabimo popravljati obliko kopice na vsakem koraku. Pri združevanju dveh kopic samo dvosmerno povežemo korena kopic (kazalce smiselno prevežemo tako, da dobimo iz dveh samo en cikel).

• Da dosežemo željen čas izvajanja, moramo na neki točki kopico urediti. V splošnem je stopnja vozlišč (t.j. število sinov) nizka. Vsako vozlišče je stopnje , kjer je število vseh vozlišč, in velikost poddrevesa vozlišča stopnje je najmanj , kjer je k-ti element Fibonaccijevega zaporedja (od tod ime Fibonaccijeva kopica). To je zaradi pravila, da lahko odstranimo vselej največ enega otroka vozlišču, ki pa ne sme biti koren. Če odstranimo še drugega otroka, potem vozlišče postane koren Fibonaccijeve kopice.

Lastnosti

1. Vsa vozlišča na istem nivoju (vozlišča, ki imajo istega očeta) so povezani dvosmerno in ciklično.
2. Fibonaccijeva kopica vsebuje kazalec na vozlišče z minimalnim ključem (izhaja iz tega, da ima drevo lastnost minimalne kopice).
3. Do kopice dostopamo preko vozlišča, ki vsebuje minimalni ključ.
4. Za vsako vozlišče beležimo njegovo stopnjo, ki je enaka številu otrok, ki jih ima. Beležimo tudi, ali je vozlišče označeno ali ni. Tu ima vrednost 1, če je označeno in 0, če ni označeno. Označenost potrebujemo pri nekaterih operacijah na kopici. Koren ni nikoli označen. Označimo le tisto vozlišče, ki ni koren in ki je izgubilo otroka (ali je bil otrok odrezan in postavljen med korene, ali izbrisan). Vozlišče odznačimo, ko postane koren. Pri nekaterih operacijah potem označena vozlišča premaknemo v koren kopice.

Fibonaccijeva kopica ima v primerjavi z binomsko kopico veliko bolj fleksibilno obliko, ker so drevesa v njej neurejena (nimajo predpisane oblike).

Operacije na Fibonaccijevih kopicah

• iskanje minimuma
• brisanje minimuma
• vstavljanje novega vozlišča v kopico
• zmanjšanje ključa v drevesu
• unija dveh kopic
• brisanje vozlišča

Novo vozlišče vstavimo v Fibonaccijevo kopico tako, da najprej naredimo novo Fibonaccijevo kopico, v katero vstavimo samo nov ključ in ju združimo tako, da novo kopico dodamo na vedno levo stran vozlišča z najmanjšim ključem. Preverimo, ali se je spremenil minimalni ključ in po potrebi popravimo kazalec, ki kaže nanj. Časovna zahtevnost operacije je O(1).

Primer:

Iskanje minimuma je trivialno, saj nam kazalec že kaže na vozlišče z najmanjšim ključem v kopici. Časovna zahtevnost operacije je O(1).

Primer:

Iskanje minimuma

Iskanje minimuma

Brisanje minimuma poteka v štirih korakih:

1. Poiščemo vozlišče z najmanjšim ključem in ga odstranimo.
2. Otroci odstranjenega vozlišča postanejo koreni Fibonaccijeve kopice.
3. Poiščemo nov minimum (vozlišče z najmanjšim ključem). Najprej zmanjšamo število vozlišč v korenu tako, da združimo tiste z isto stopnjo. Če imamo vozlišči z isto stopnjo, postane tisto z manjšim ključem starš tistemu z večjim ključem. Če obstajata več kot dve vozlišči z isto stopnjo, vrstni red združevanja ni pomemben. Recimo, da stopnje vozlišč preverjamo od leve proti desni gledano od minimuma naprej. To ponavljamo toliko časa, dokler nimajo vsa vozlišča v korenu različne stopnje.
4. Za konec še preverimo ključe vozlišč v korenu in označimo minimum. Časovna zahtevnost operacije je .

Primer: (Aplikacija je takšna, da nam da sinove izbrisanega vozlišča na konec na desno stran. Za "pomožni" minimum nastavi skrajno desno vozlišče. Zato začne gledati najprej čisto desno vozlišče, potem prvega na levi strani,…)

Pri združevanju dveh Fibonaccijevih kopic lahko ločimo več možnosti:

• Ena Fibonaccijeva kopica je prazna, druga pa ni (to enostavno preverimo tako, da pogledamo ali obstaja vozlišče z minimilnim ključem). Potem je unija teh dveh kopic kar neprazna kopica.
• Unija dveh praznih Fibonaccijevih kopic je prazna Fibonaccijeva kopica.
• Primer je zanimiv le, če sta obe kopici neprazni. Korenu prve kopice dodamo vozlišča iz korena druge kopice. Preveriti moramo še, kateri izmed obeh najmanjših ključev je najmanjši ključ v novo nastali kopici in tistega označimo kot minimum. Časovna zahtevnost operacije je .

Primer:

OPOMBA: Zeleno označena vozlišča so pomembna pri drugih operacijah na Fibonaccijevih kopicah (glej operaciji Zmanjšanje ključa in Izbriši vozlišče). Pri uniji nimajo nobene posebne vloge.

Operacijo začnemo tako, da najprej izberemo vozlišče, katerega ključ želimo zmanjšati. Ko ga zmanjšamo, preverimo, če se lastnosti kopice spremenijo. Če je spremenjen ključ še vedno večji od ključa očeta, ni potrebnih nobenih nadaljnih popravkov. Če pa postane spremenjeni ključ manjši od ključa očeta, vozlišče odcepimo od starša in ga prestavimo v koren, ter označimo njegovega starša (označevalni bit iz 0 spremenimo v 1, oziroma vozlišče pobarvamo z zeleno barvo). Če je bil oče že prej označen, ga prav tako odcepimo, prestavimo v koren in označimo njegovega očeta. Nadaljujemo na tak način, vse dokler ne pridemo do korena ali pa do neoznačenega vozlišča. Odcepljena vozlišča se priključijo v koren kopice. Časovna zahtevnost operacije je .

Primer:

Brisanje vozlišča je kombinacija operacij zmanjšanje ključa in brisanje minimuma. Vozlišču, ki ga hočemo zbrisat, najprej zmanjšamo ključ na število, ki je manjše od trenutnega minimuma. Enako kot pri zmanjšanju ključa pogledamo in po potrebi odcepimo še njegovega očeta, če je le ta označen. Izbrano vozlišče, ki se sedaj nahaja v korenu (in je tudi minimum), zbrišemo tako, da dobljeni Fibonaccijevi kopici zbrišemo minimum. Časovna zahtevnost operacije je , ker je tudi operacija brisanje minimuma časovne zahtevnosti .

Primer:

Po vseh operacijah dobimo kot rezultat še vedno Fibonaccijevo kopico, saj smo sinove vozlišč z manjšim ključem (od ključa vozlišča) takoj premestili v koren. Pri nekaterih operacijah smo tudi popravili obliko kopice, vendar je v splošnem lahko oblika precej poljubna in ne vpliva na to, da je to res Fibonaccijeva kopica (kot en ekstremen primer je že navedeno, da se lahko tudi vsa vozlišča nahajajo v korenu kopice).

Prikaz dela z Java aplikacijo:

1.Kakšno kopico dobimo, če zbrišemo minimum?

Preveri

Pravilno poveži, kakšne časovne zahtevnosti imajo operacije!

Preveri

Trdimo, da so Fibonaccijeve kopice sestavljene iz dreves, ki imajo lastnost minimalne kopice. To pomeni, da

Preveri

• http://en.wikipedia.org/wiki/Fibonacci_heap

• http://wiki.fmf.uni-lj.si/wiki/Fibonaccijeva_kopica

• Java aplikacija za delo s Fibonaccijevo kopico