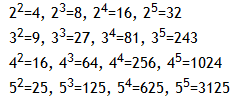Metodo začnemo z ukazom def
, nato napišemo ime metode, ter v oklepaju parametre.
Ustvarimo prazen seznam c
, v katerega bomo shranjevali tista števila, ki jih še ni v seznamu.
Nadaljujemo s for
zanko (v navodilih piše , jaz pa sem uporabla ), ki nastvimo vrednost x, torej osnovi, naslednja for zanka pa nastavlja vrednosti potence. Za vsak x bo 'dobil' potenco, ki zavzema vrednsoti od 2 do b, kjer je b zgornja meja za vrednosti y.
Nato postavimo stavek if. Prverjali bomo, če je element že v seznamu ali še ne. Torej if x**y not in c:
. Če je pogoj izpolnjen, torej element še ni v seznamu c, ga dodamo v seznam c, se pravi: c.append(x**y)
, v nasprotnem primeru ne storimo nič. Ker smo v seznam c dodajali sama različna števila, je rezultat naloge kar dolžina seznama c. Izračunamo jo s pomočjo ukaza len(c) (len, kot length). Zapišemo: retunrn len(c)
.
Tako izgleda metoda, ko končamo njeno konstrukcijo.