V enakokrakem trapezu ABCD merita osnovnici |AB| = a = 7, |CD| = c = 3, diagonali e=f= .

• Izračunajte višino in krak b v trapezu ABCD (napišite točna rezultata)
• Izračunajte kot med diagonalama trapeza ABCD (rezultat zaokrožite na stotinko stopinje)
• Trapez ABCD zavrtimo okoli krajše osnovnice c. Izračunajte površino in prostornino tako nastalega rotacijskega telesa. (Zapišite točna rezultata)

Najprej sem si na list papirja skicirala trapez, ter označila vse podatke, ki so podani, označila pa sem tudi stvari, ki jih je bilo potrebno izračunati.

Najprej sem si na novo narisala trikotnik z daljšo stranico trapeza, enim krakom in ustrezno diagonalo. S pomočjo te skice sem izračunala višino trapeza. Višino trapeza sem izračunala s pomočjo Pitagorovega izreka , torej v mojem primeru ; , torej je . Dolžino katete sem ravno tako izračunala s pomočjo Pitagorovega izreka: ; , torej je .

Ta del naloge sem skonstruirala še v Geogebri. To sem storila tako, da sem najprej narisala daljšo stranico osnovnice s točkama in . Nato sem narisala višino trapeza, tako da sem narisala točko . Narisala sem še točko C, tako da je krajša stranica dolga 3. Nato sem narisala še kraka, in preverila če sem izračunala pravilno dolžino le-teh; to sem storila z ukazom Razdalja od točke A do D in od točke B do C. Po istem postopku sem narisala še diagonali e in f, le da sem tu merila razdaljo med nasproti ležečima točkama, tj. med A in C ter med B in D.

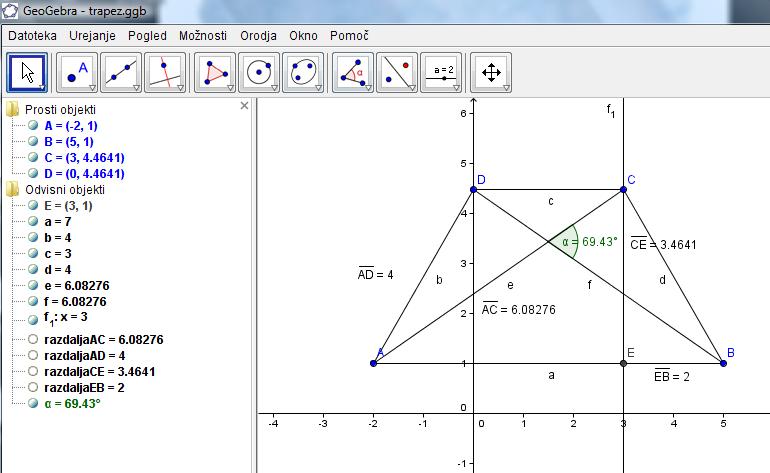
S pomočjo Geogebre sem izračunala tudi pod kakšnim kotom se sekata diagonali e in f. Pri tem sem si pomagala z ukazom Kot med f in e in ugotovila da se diagonali sekata pod kotom .

Ko enakokraki trapez zavrtimo okrog krajše osnovnice c dobimo valj z luknjo v obliki valja – »cev«. Površino takega telesa izračunamo tako, da seštejemo ploščino osnovne ploskve (krog), plašč zunanjega valja in plašč notranjega valja. Volumen takega telesa pa izračunamo tako, da od volumna zunanjega valja odštejemo volumen notranjega valja.

Polmer zunanjega valja, je kar višina trapeza, torej je , polmer notranjega valja pa je enak razliki osnovnic, tj. . Višina obeh valjev je enaka dolžini daljše osnovnice a, tj. . Torej je volumen zunanjega valja naslednji: , volumen notranjega valja pa: . Od tod sledi, da je skupni volumen vrtenine enak . Plašč notranjega valja izračunamo po naslednji formuli: plašč = . Površino zunanjega pa: . Torej je površina »cevi« naslednja: , kjer je ploščina osnovnih ploskev notranjega valja.