Dani sta kvadratni funkciji in .
a) Narišite grafa obeh funkcij v dani koordinatni sistem.
b) Izračunajte presečišči grafov danih funkcij.
c) Izračunajte in .
4. Naloga
4. Naloga
Marina Pijetlović
Besedilo naloge
Poteke reševanja "na roke"
Če hočemo narisati funkciji in , moramo najprej izračunati ničle, začetno vrednost in teme.
Ničle:
Začetna vrednost:
Teme:
Ničle:
Začetna vrednost:
Teme:
Presečišči obeh funkcij izračunamo tako, da enačbi enačimo.
(enačbo pomnožimo z 2)
(enačbo delimo s 3)
Da dobimo še y1 in y2, moramo x1 in x2 vstaviti v eno izmed enačb.
Imamo dve presečišči. Prvo je točka in pa .
Izračunati še moramo in pa . To naredim tako, da v funkcijo namesto x-a vstavimo 2, v funkcijo pa namesto x-a vstavimo -1.
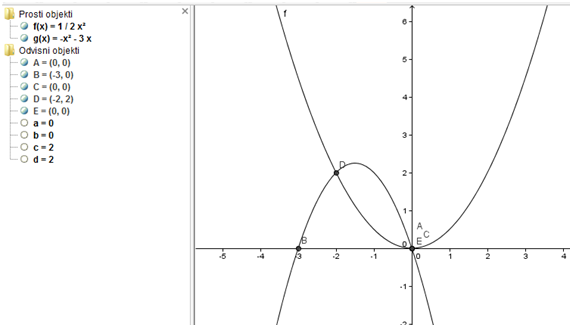
Nalogo lahko rešimo tudi v Geogebri in sicer tako, da v program vnesemo obe funkciji:
in , ki nam nariše obe paraboli. Nato določimo ničle obeh funkcij z ukazom Ničla[f(x)] (= A) in Ničla[g(x)] (= B). Z ukazom (= a) in (= b) določimo začetno vrednost, izračunamo pa tudi (= c) in pa ) (= d). Presečišče funkcij dobimo z ukazom Presečišče[f(x), g(x)], to sta točki D in E.
- Besedilo naloge
- Poteke reševanja "na roke"
- Presečišči obeh funkcij izračunamo tako, da enačbi enačimo.
- Da dobimo še y1 in y2, moramo x1 in x2 vstaviti v eno izmed enačb.
- Izračunati še moramo in pa . To naredim tako, da v funkcijo namesto x-a vstavimo 2, v funkcijo pa namesto x-a vstavimo -1.
- Nalogo lahko rešimo tudi v Geogebri in sicer tako, da v program vnesemo obe funkciji:
