Besedilo naloge
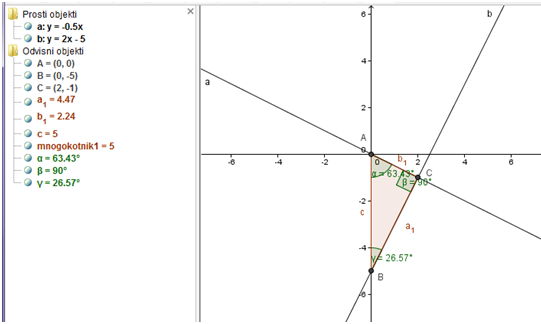
Dani sta premici: in .
a) Premici narišite v isti koordinatni sistem, označite njuno presečišče in izračunajte njegovi koordinati.
b) Izračunajte kot med premicama.
c) Premici in ordinatna os določajo trikotnik. Izračunajte dolžino najkrajše stranice in ploščino tega trikotnika.
Najprej izpostavimo y iz premic.
1. premica
2. premica
Če želimo narisati premici, moramo izračunati skozi katere točke gre. Za premico si moramo izbrati najmanj dve točki.
1. premica
| x | y |
| 1 | |
| 0 | 0 |
2. premica
| x | y |
| 1 | -3 |
| 0 | -5 |
Presečišče premic izračunamo tako, da ju enačimo:
(pomnožimo z 2)
(delimo s 5)
Ta x, ki smo ga dobili, vstavimo v eno izmed enačb, da dobimo še y.
Premici se sekata v točki C (2, -1).
Kot med premicama
Ker velja, če je se premici sekata pod pravim kotom. In seveda v našem primeru to velja.
Kot med premicama :
Iz skice lahko vidimo, kje leži trikotnik. Najkrajša stranica b1, je na 1. premici med točkama A in C. Ker poznamo točko in lahko izračunamo dolžino stranice b1.
Torej,
Ploščina pravokotnega trikotnika
Ploščino pravokotnega trikotnika izračunamo po formuli . Ker stranice a1 nimamo podane, jo lahko izračunamo po pitagorovem izreku.
Za stranico c1 vemo, da je dolga 5, saj je . Podatke vstavimo v formulo za ploščino
Nalogo, lahko rešimo tudi v Geogebri.
V program vnesemo obe premici in . Označimo presečišča, kjer se premici sekata in pa kjer sekata ordinatno os, da dobimo dani trikotnik. Z ukazom Mnogokotnik[A, B, C] označimo trikotnik in tako dobimo dolžine stranic ter ploščino trikotnika. Z ukazom Kot[] dobimo vrednosti kotov. Če primerjamo vrednosti, ki smo jih dobili v Geogebri in vrednosti, ki smo jih sami izračunali, vidimo da se ujemajo.
