Če bi gladina svetovnih morij in oceanov narasla, bi se lahko kakšen otok popolnoma potopil in bi se tako število otokov na svetu zmanjšalo za ena. Po drugi strani pa bi lahko pri kakšnem otoku voda zalila le nižje ležeče dele, hribi pa bi še vedno štrleli ven in bi tako iz enega nastalo več samostojnih otokov; tako bi se število otokov na svetu povečalo. Podobno je, če se gladina oceanov zniža— kakšen otok lahko na novo pogleda iz vode, lahko pa se več otokov združi v enega samega, ker se plitvine med njimi izsušijo. Tako se torej, če spreminjamo gladino oceanov, število otokov zdaj povečuje, zdaj zmanjšuje. Nas pa zanima, kakšno je največje število otokov, ki bi ga lahko na svetu imeli, če bi mogli primerno izbrati gladino oceanov. (Za potrebe te naloge štejemo tudi celine kot velike otoke.)

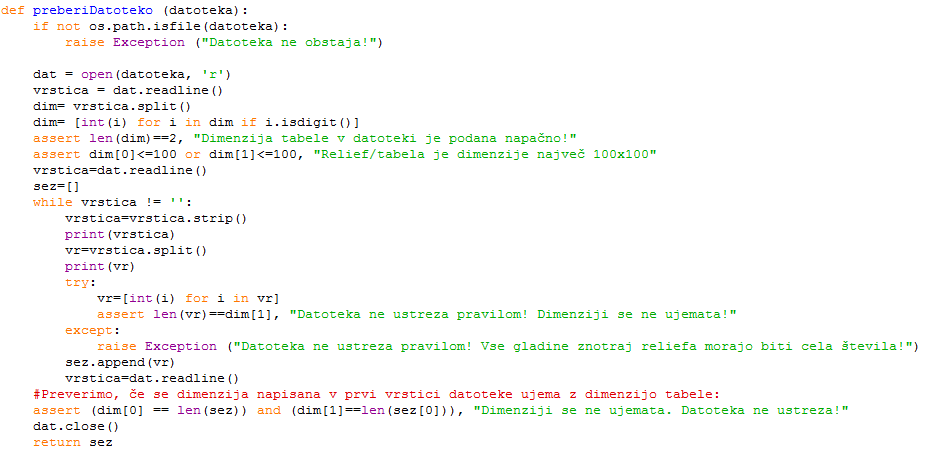
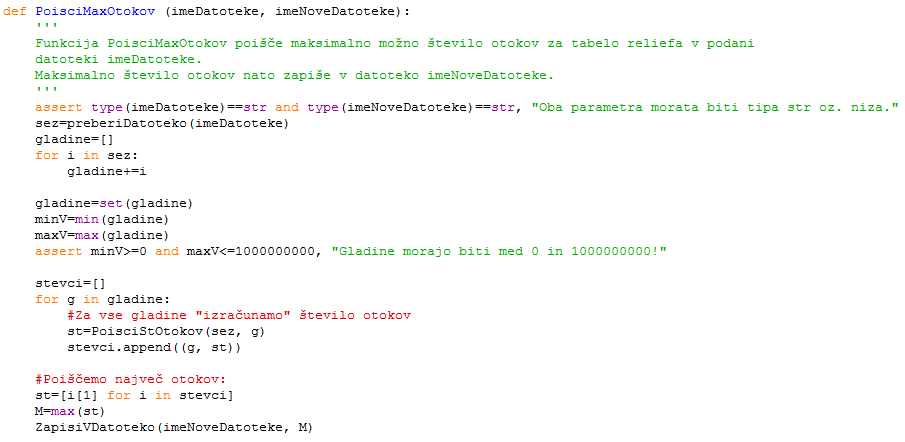
Da bo naloga lažja, predpostavimo, da je Zemlja ploščata, ne pa okrogla, in da je njeno površje kot karirasta mreža, v kateri je višina površja znotraj vsake celice konstantna. Naj bo v(x, y) višina celice na preseku vrstice y in stolpca x. Če je gladina oceanov g, si mislimo, da so vse celice (x, y), za katere je v(x, y) < g, potopljene pod vodo, vse ostale pa so kopne. Pri tej nalogi torej ne bomo komplicirali z jezeri, depresijami, rečnimi in jezerskimi otoki ipd. Otok definirajmo kot vsako tako skupino kopnih celic, ki je povezana (torej se da priti od poljubne celice otoka do poljubne druge celice otoka, pri tem pa ves čas hoditi po samih kopnih celicah in iti vedno s trenutne celice na eno od njenih štirih sosed, ki imajo z njo skupnega enega od robov) in ki ji ne moremo dodati nobene druge trenutno kopne celice, ne da bi ta pogoj prenehal veljati. (Glej primer spodaj.) Napiši program, ki pri danih podatkih o višinah ugotovi, katero je največje možno število otokov, ki jih je mogoče dobiti s primernim izborom gladine oceanov g.

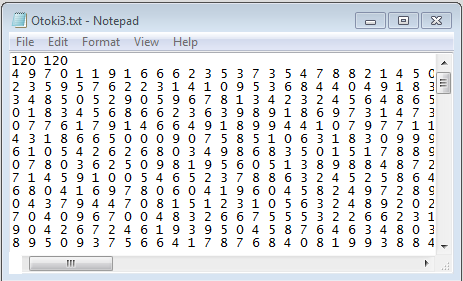
Vhodna datoteka: v prvi vrstici sta najprej števili h in w, ki povesta višino oz. širino kariraste mreže. To sta celi števili, velja 1 <= h <=100, 1 <=w <=100. Sledi h vrstic, v vsaki je po w števil, ki povedo višine celic: v(1, y), v(2, y), . . . , v(w, y). Višine so cela števila, zanje velja 0 <=v(x, y)<= 1 000 000 000.
Izhodna datoteka: vanjo naj tvoj program izpiše največje možno število otokov, ki ga je mogoče pri dani vhodni datoteki dobiti, če primerno izberemo gladino oceanov g.

Primer vhodne datoteke:
5 10
6 6 8 6 3 4 2 3 6 7
3 7 9 7 3 3 3 2 6 6
3 6 7 7 2 2 6 5 5 6
5 5 5 2 2 5 5 8 5 5
5 6 5 1 0 3 4 4 4 3
Pripadajoča izhodna datoteka:
5

Potrebovali bomo:

• Funkcijo, ki prebere datoteko,
• funkcijo, ki za dan relief in gladino poišče število otokov,
• funkcijo, ki za dan seznam poišče maksimalno število otokov,
• funkcijo, ki maksimalno število otokov zapiše v datoteko.

Problem – Kako poiskati maksimalno število otokov?

Število otokov pri različnih gladinah ni odvisno med seboj, zato nam rešitev pri neki gladini ne more pomagati pri računanju neke druge gladine. Tako moramo število otokov izračunati za vsako gladino posebej.

Sedaj moramo samo še razmisliti, kako dobiti število otokov pri neki gladini. Sprehodimo se čez seznam sez. Ko pridemo do novega koščka kopnega, smo našli nov otok. Poiščemo vse točke oz. elemente seznama, ki pripadajo temu koščku in jih označimo. Sprehod nadaljujemo na naslednjem polju začetnega kopnega.

Potrebovali bomo pet funkcij:

• preberiDatoteko(datoteka)
• ZapolniSez(sez,vr,st,g)
• PoisciStOtokov(sez1,g)
• PoisciMaxOtokov(imeDatoteke, imeNoveDatoteke)
• ZapisiVDatoteko(sez1, g)

Funkcija sprejme en parameter, ime datoteke.

S pomočjo te funkcije bomo dobili seznam, ki bo vseboval relief. Najprej preverimo, če datoteka sploh obstaja. V nasprotnem primeru sprožimo napako.

• uvozimo knjižnico os
• os.path.isfile(imeDatoteke) vrne True, če datoteka obstaja oz. False, če ne.

Sedaj lahko odpremo datoteko za branje.

• dat=open(imeDatoteke, 'r')

Posamezne vrstice bomo brali z metodo dat.readline().

Ko začnemo brati, pazimo, da prva vrstica vsebuje podatke o dimenzijah. Zato prva vrstica ne pride v poštev za v seznam. Shranimo jo v nov seznam, ki ga poimenujemo dim. Seveda moramo prej razbiti niz, ki smo ga prebrali (dat.readline()).
Pomagamo si s funkcijami oz. metodami:

• dim=vrstica.split() – »razbijemo« niz vrstica v seznam glede na bele znake
• i.isdigit() – vrne True, če je niz i vsebuje vsaj en znak in so vsi znaki števke
• int(i) – pretvori niz v celo število
• dim=[int(i) for i in dim if i.isdigit] – seznamski izraz --> »sprehodi« se čez seznam dim. Če je element i, ki je tipa niz, število, potem niz i pretvori v tip int (celo število) in ga doda novemu seznamu dim (poimenujemo enako). To deluje, ker Python vedno najprej izvede desno stran izraza, nato pa šele priredi vrednost na levi.

Preverimo dolžino seznama dim: Vemo, da mora biti dolžina seznama dim 2, ker je naša tabela reliefa velikosti nxm. Če dolžina seznama ne ustreza, sprožimo napako.
Ko imamo dimenzije, preverimo, če je dimenzija tabele manjša ali enaka dimenziji 100x100. Če je tabela večje, sprožimo napako.

Nazaj k branju datoteke. Kot smo že omenili, beremo vsako vrstico posebej (dat.readline()). Ko preberemo vrstico, dobimo niz, torej moramo niz spremeniti v seznam znakov. A prej odstranimo bele znake (niz.strip()). Nato z metodo split naredimo seznam znakov prebrane vrstice.

Sedaj imamo vrstico tabele reliefa že kot seznam. Vsi elementi so nizi, zato jih spremenimo v cela števila. To naredimo s pomočjo seznamskega izraza [int(i) for i in vr]. Ta stavek/izraz zapišemo znotraj mreže try/except. Predvidevamo, da bo prišlo lahko do napake, če element ne bo število. Če element ne bo celo število, bo prišlo do napake pri pretvarjanju z metodo int. Napako bo ujel except stavek. Znotraj except-a sprožimo lastno napako s pomočjo raise Exception z opozorilom, da morajo biti elementi tabele reliefa izključno cela števila.
Znotraj mreže try, pa za seznamskim izrazom preverimo še, če je vrstica pravilne dolžine oz. če se ujema z dano dimenzijo prve vrstice.

Če se vse izvrši pravilno in ne pride do napak je vrstica (seznam vr) pravilne oblike. Dodamo jo seznamu sez. Preberemo novo vrstico.
Postopek se zaključi, ko je prebrana vrstica prazen niz.

Ko imamo seznam, najprej preverimo, če je datoteka smiselna (da bo program čim bolj stabilen). Torej, če se ujemajo podane dimenzije z dimenzijo seznama. Če seznam ne ustreza pravilom, sprožimo napako.

Če ne pride do napake in se celotna funkcija izvrši, zapremo datoteko in vrnemo seznam sez.

Uporabljene funkcije/metode:

• os.path.isfile(datoteka) – Vrne True, če datoteka v trenutni mapi obstaja oz. vrne False, če datoteka ne obstaja v trenutni mapi/direktoriju.
• dat=open(datoteka, 'r') - odpre datoteko za branje
• vrstica=dat.readline()– prebere (trenutno) vrstico iz datoteke
• vrstica.split() – metoda split »razbije« niz vrstica glede na bele znake v seznam in ga vrne
• assert pogoj, 'sporočilo ob sprožitvi napake, če pogoj ne drži'
• vrstica.strip() – vrne niz vrstica, vendar mu prej »odreže« bele znake na začetku in na koncu niza
• [int(i) for i in vr] – naredi/vrne seznam identične seznamu vr, le da elemente vr pretvori v cela števila
• raise Exception ("Sporočilo ob sprožitvi izjeme") - sproži izjemo s sporočilom
• sez.append(vr) - seznam vr doda kot nov element na konec seznama sez
• len(seznam) - vrne dolžino seznama oz. če je seznam dvodimenzionalen vrne število vrstic
• len(seznam[0]) - vrne 'število stolpcev'
• dat.close() - zapre datoteko

Funkcija ZapolniSez(sez, vr, st,g) sprejme seznam reliefa, drugi in tretji parameter predstavljata lokacijo kopnega. Okrog lokacije poiščemo še ostalo kopno, ki se je drži in ga označimo s posebnim znakom. Četrti parameter je višina gladine.

Kot smo že zgoraj omenili bo funkcija zapolnila s posebni znakom ('+') kopno okoli podane lokacije (če je podana lokacija res kopno).

Ustavitveni pogoji:

Vprašamo se, kaj vse mora nujno »ustaviti funkcijo«. Funkcija se ustavi če:

• je podana lokacija izven tabele
• je lokacija že zapolnjena z znakom '+' ali če je lokacija pod gladino.

Če kateri od ustavitvenih pogojev velja, kličemo samo return (končamo funkcijo, seznam se ne spremeni).

Rekurzivno klicanje – funkcija kliče samo sebe

Če se funkcija ne ustavi pri nobenem od ustavitvenih pogojev, štirikrat rekurzivno pokličemo polja okoli nas:

• Za pozicijo nad nami povečamo vrstico (parameter vr) za ena, stolpec (parameter st) ostane enak.
• Za pozicijo pod nami zmanjšamo vrstico za ena, stolpec je enak.
• Za pozicijo levo od trenutne zmanjšamo stolpec za ena, vrstica ostane enaka.
• Za pozicijo desno od trenutne povečamo stolpec za 1, vrstica ostane enaka.

Funkcija ne vrača ničesar, samo spreminja podan seznam.

Funkcija sprejme seznam sez1 in višino gladine g.
Nujno je potrebno, da naredimo globoko kopijo podanega seznama, saj bomo seznam spreminjali.

• Uvozimo knjižnico copy

• sez=copy.deepcopy(sez1)

  • Globoko zato, ker so tudi elementi seznama seznami/objekti.

Definiramo števec st=0, ki bo štel število otokov za dano gladino.
S for zanko se sprehodimo čez seznam sez. Ko pridemo do elementa seznama, ki je nov košček kopnega, smo našli nov otok. Poiščemo vso kopno, ki se drži tega elementa. To naredimo s pomočjo funkcije ZapolniSez. Števec st povečamo za ena. Sprehod nadaljujemo na naslednjem polju začetnega kopnega.
Vrnemo števec st.

Uporabljene funkcije/metode:

• copy.deepcopy(sez1) vrne nov objekt, ki je "globoka" kopija objekta seznama sez1 (tudi elementi sez1, ki so objekti, so v kopiji novi objekti)

Funkcija sprejme ime datoteke (ime) in celo število (st), ki ga želimo zapisati.
Najprej bomo preverili, če datoteka, ki jo želimo ustvariti, že obstaja. Če obstaja, uporabnika toliko časa sprašujemo za novo ime, dokler to ime za datoteko še ne obstaja v trenutnem direktorju. Če tega ne bi preverjali, bi se prejšnja istoimenska datoteka prepisala.
Ko vemo, da bomo varno ustvarili datoteko, le-to ustvarimo.

• dat=open(imeDatoteke, 'w')

  • S parametrom 'w' povemo, da bomo datoteko odprli za pisanje.

S pomočjo klica funkcije dat.write(str(st)) zapišemo število v datoteko. str(st) dodamo zato, ker moramo metodi write() podati parameter tipa niz.
Na koncu samo še zapremo datoteko (dat.close()).

Uporabljene funkcije/metode:

• type(ime) - vrne tip podanega parametra

  • niz je str
  • celo število je int
• input("Novo ime: ") - program uporabnika vpraša za novo ime. Vrne uporabnikov vnos
• open (ime, 'w') - ustvari datoteko z imenom ime in jo odpre za pisanje
• str(st) - število st pretvori v niz
• dat.write(str(st)) - zapiše niz v datoteko
• dat.close() - zapre datoteko

Funkcija sprejme ime vhodne (imeDatoteke) in ime izhodne datoteke(imeNoveDatoteke).

Za dano vhodno datoteko zapiše novo datoteko z imenom imeNoveDatoteke v katero zapiše maksimalno število otokov.

Sedaj imamo pripravljene oz. definirane funkcije, ki jih bomo potrebovali.

Najprej s pomočjo funkcije preberiIzDatoteke(imeDatoteke) dobimo seznam reliefa sez.

Nato moramo za vsako gladino znotraj reliefa izračunati število otokov.
Kako dobiti vse gladine, ki nastopajo v reliefu?
Pomagamo si s funkcijo, ki nam iz seznama naredi množico (set(seznam)).

• Funkcijo set lahko uporabimo samo na enodimenzionalnem seznamu, zato moramo najprej naš seznam sez najprej preurediti v enodimenzionalnega.
• Dobljen nov seznam poimenujemo gladine.

Sedaj imamo enodimenzionalni seznam gladine. Uporabimo funkcijo set.

• gladine = set(gladine)

Nato poiščemo maksimalno in minimalno gladino. Pomagamo si s funkcijama min in max:

• maxV=max(gladine)
• minV=min(gladine)
• Če je minV manjša od 0 sprožimo napako.
• Če je maxV večja od 1000000000 sprožimo napako.

Definiramo še prazen seznam stevci, kamor bomo vpisovali število otokov za dano gladino.

Sedaj za vsako gladino v množici gladine izračunamo število otokov.

• To naredimo tako, da se sprehodimo s for zanko čez množico gladine.
• Znotraj for zanke tako za vsako gladino kličemo PoisciStOtokov(sez, g).
• Dobljeno število otokov in gladino dodamo kot dvojico v seznam stevci.

Sedaj s pomočjo seznama stevci definiramo nov seznam st, ki bo vseboval samo število otokov.

• st=[i[1] for i in stevci]

Poiščemo maksimalen element seznama st in ga shranimo v spremenljivko M.

Za konec samo še pokličemo funkcijo ZapisiVDatoteko(imeNoveDatoteke, M), ki nam zapiše število M v datoteko.

Python datoteka

S testiranjem bomo preverili, če se funkcija »obnaša« pravilno oz. tako kot bi pričakovali.
Kot bomo videli kasneje si bomo pomagali z varovalnimi mrežami try, except (stavek except: polovi vse napake znotraj try-a.)

V primeru, da funkcijo kličemo pravilno in ne pričakujemo napak, uporabimo naslednjo kodo:
try:
    klic funkcije
except Exception as e:
    print ('Prišlo je do napake!')
    print(e)

Če se bo funkcija pravilno izvršila, se nam na ekran ne bo izpisalo nič. Če pa bo ob klicu prišlo do napake, bo napako ulovil stavek Except. Izpisalo se bo sporočilo 'Prišlo je do napake!' in izpisal se bo tudi opis napake (e), ki ga vrne Python.

V primeru, da pričakujemo oz. vemo, da mora funkcija sprožiti napako uporabimo kodo:
try:
    klic funkcije
    print('V ta print ne bi smelo priti!')
except:
    pass

Ker pričakujemo, da bo ob neustreznih parametrih prišlo do napake ob klicu funkcije, za klicem spišemo nek stavek print. Če bo vse prav in bo do napake res prišlo, se ta print ne bo izvedel. Če se bo print izvedel, to pomeni, da funkcija ni sprožila napake in da je posledično spisana narobe. Če se bo zgodilo pričakovano, torej če se bo sprožila napaka, vemo, da bo stavek except »ulovil« napako. Zato stavek pass, ki ne naredi ničesar, saj je prav, da se je sprožila napaka.

Glede na to kakšen primer testiramo, v testno datoteko spišemo kodo kot v zgornjih dveh primerih. Ko imamo spisane vse try, except stavke in smo z njimi res preverili vse možne primere, smo končali s pisanjem testne datoteke. Izvršimo testno datoteko (pritisnemo F5). Če se v Python Shell-u ne izpiše nič, to pomeni, da se funkcija obnaša pravilno.

• Odpremo novo Python datoteko.

• Uvozimo metode/funkcije iz Python datoteke, kjer se nahaja naša testirana funkcija:

  • import Otoki

• Stestiramo osnovne primere

  • Primer, ki je podan znotraj naloge (Otoki.txt)

  • Zelo osnoven primer reliefa (Otoki1.txt)

    • Če bi si izmislili večjo datoteko, bi zelo težko preverili rezultat na peš.

• Stestiramo primere, kjer pričakujemo, da funkcija vrne napako.

  • Podani napačni parametri (oba parametra, ki jih funkcija sprejme, sta imeni datotek, zato morata biti niz).

  • Vsebina datoteke je nepravilna:

    • primer z neujemanjem dimenzij (Otoki2.txt)
    • primer prevelikega reliefa (dovoljujemo le 100x100) (Otoki3.txt)
    • primer, kjer v reliefu niso same cifre (Otoki4.txt)
    • primer, kjer so v reliefu podane nedovoljene gladine (Otoki5.txt)

• Za vhodno datoteko podamo datoteko, ki ustreza pravilom (prva vrstica predstavlja dimenzije, naslednje vrstice pa tabelo)
• Za izhodno datoteko pravilno podamo ime datoteke (niz)

• Naredimo oba primera z datotekama Otoki.txt in Otoki1.txt

  • Preverimo, če se ugotovitve ujemajo

Primer dveh pravilnih datotek in klicev funkcij:

Otoki.txt:

datoteka Otoki.txt

Klic funkcije: Otoki.PoisciMaxOtokov('Otoki.txt', 'Izh.txt')
Pričakujemo, da se bo v Izh.txt zapisala petica (5).

Otoki1.txt:

datoteka Otoki1.txt

Klic funkcije: Otoki.PoisciMaxOtokov('Otoki1.txt', 'Izh1.txt')
Pričakujemo, da se bo v datoteki Izh1.txt prav tako zapisala petica(5).

Komentar in koda:

Ker v obeh primerih pričakujemo, da ne bo prišlo do napake, bomo uporabili prvi način uporabe varovalne mreže try, except.
try:
    Otoki.PoisciMaxOtokov('Otoki.txt', 'Izh.txt«)
except Exception as e:
    print ('Prišlo je do napake!')
    print(e)

try:
    Otoki.PoisciMaxOtokov('Otoki1.txt', 'Izh1.txt')
except Exception as e:
    print ('Prišlo je do napake!')
    print(e)

Stestiramo primere, kjer pričakujemo, da funkcija vrne napako.

• Vprašamo se, kdaj mora funkcija sprožiti napako.

  • Ločimo dva primera:

    • napačni prametri (oba parametra morata biti tipa niz)
    • vhodna datoteka ne ustreza pravilom (napačna dimenzija, prevelika tabela, nedovoljeni znaki, nedovoljene gladine)

Uporabljali bomo drugi način uporabe varovalne mreže.

Funkcijo na primer pokličemo Zapolni(8,9).

• Funkcija mora sprožiti napako - oba parametra morata biti niza
  try:
      Otoki.PoisciMaxOtokov(8, 9)
      print('V ta print ne bi smelo priti!')
  except:
      pass
  

Neujemanje dimenzij

Preverimo, če funkcija sproži napako, kadar se podana dimenzija v prvi vrstici datoteke razlikuje od dejanske dimenzije tabele. Primer take datoteke je Otoki2.txt, kjer je dejanska dimenzija tabele 5x10.

Otoki2.txt:

datoteka Otoki.txt

Varovalna mreža in klic funkcije:
try:
    Otoki.PoisciMaxOtokov('Otoki2.txt', 'Izh2.txt')
    print(‘V ta print ne bi smelo priti!’)
except:
    pass

Prevelika tabela

Funkcija zahteva, da je maksimalna tabela velikosti 100x100.
Primer datoteke, ki vsebuje tabelo večjo od 100x100 , je Otoki3.txt:

datoteka Otoki3.txt

Varovalna mreža in klic funkcije:
try:
    Otoki.PoisciMaxOtokov('Otoki3.txt', 'Izh3.txt')
    print(‘V ta print ne bi smelo priti!’)
except:
    pass

Nedovoljeni znaki znotraj tabele

Funkcija dovoljuje znotraj tabele cela števila.
Preverimo, če vrne napako, kadar zgornja trditev ne drži.
Taka datoteka je Otoki4.txt:

datoteka Otoki4.txt

Varovalna mreža in klic funkcije:
try:
    Otoki.PoisciMaxOtokov('Otoki4.txt', 'Izh4.txt')
    print('V ta print ne bi smelo priti!')
except:
    pass

Nedovoljene gladine

Funkcija dovoljuje znotraj tabele cela števila od 0 do 1000000000.
Preverimo, če vrne napako, kadar zgornja trditev ne drži.
Taka datoteka je Otoki5.txt:

datoteka Otoki5.txt

Varovalna mreža in klic funkcije:
try:
    Otoki.PoisciMaxOtokov('Otoki5.txt', 'Izh5.txt')
    print('V ta print ne bi smelo priti!')
except:
    pass

S testnimi primeri bomo preverili, če se funkcija obnaša pravilno v različnih primerih.
Preverimo, če se funkcija res v vseh primerih obnaša pravilno.

Zaženemo testno datoteko. Opazimo, da se v Python Shell-u ne izpiše nič. To pomeni, da funkcija gotovo v vseh primeri deluje pravilno. Preveriti moramo samo še, če so vse datoteke, ki pa so vseeno nastale, pravilne (res vsebujejo pravilno število poti).

Opazimo, da funkcija deluje pravilno.