Starting in the top left corner of a 2x2 grid, there are 6 routes (without backtracking) to the bottom right corner.

2x2 tabela

How many routes are there through a 20x20 grid?

Prevod:

V 2x2 tabeli obstaja 6 poti iz zgornjega levega oglišča do spodnjega desnega oglišča. Ne dopušča se »hoje« nazaj (premikamo se lahko le desno in navzdol).
Koliko je takih poti v 20x20 veliki tabeli?

Ena od idej je, da poiščemo vsako možno pot posebej od začetka do konca in jih preštejemo. Ta metoda je preveč »požrešna«, saj je pri velikih dimenzijah teh poti preveč.

Druga ideja je, da ko enkrat izračunamo, koliko je možnih poti od neke točke do konca tabele, si to zapomnimo in kasneje to uporabimo.
Mi se bomo osredotočili na to zadnjo idejo.

Vsaki »točki« v tabeli bo pripadal element seznama sez.

• Točka (0,0) bo pripadala elementu seznama sez --> sez[0][0].
• Točka (0,1) bo pripadala elementu seznama sez --> sez[0][1].

Če računamo poti za tabelo velikosti n x n, vemo, da ima ta tabela (n+1) x (n+1) točk. Torej bomo mi potrebovali (n+1) x (n+1) velik seznam. Vsaki točki tabele pripada element seznama.

Seznam in tabela

Ko govorimo o tabeli, mislimo na tabelo, za katero računamo število možnih poti. V našem primeru tabela velikosti 20x20.
Ko govorimo o seznamu, mislimo na objekt v katerega bomo shranjevali število poti iz določene točke/lokacije do končne točke (n-1, n-1) oz. spodnjega desnega kota.

Če se nahajamo na »običajni točki« (točki, ki ne leži na desnem ali spodnjem robu) imamo natančno dve možni poti. Lahko dostopamo do točke pod nami in do točke desno od nas.

• Na vsaki točki, ki se nahaja na desnem robu, imamo natanko eno pot oz. lahko dostopamo samo do ene točke. To je točka pod trenutno točko.

  • Torej je do spodnjega desnega kota tabele samo ena možna pot (pomikamo se lahko samo navzdol).

• Na vsaki točki, ki se nahaja na spodnjem robu, imamo natančno eno pot oz. eno možnost do naslednje točke. Lahko dostopamo le do točke desno od trenutne točke.

  • Torej je do spodnjega desnega kota tabele le ena možna pot (pomikamo se lahko samo desno).

Iz zgornjih ugotovitev je očitno, da so v našem seznamu v desnem stolpcu same enice, prav tako so same enice v zadnji vrstici. V bistvu je v spodnjem desnem kotu ničla, saj ta element seznama predstavlja končno točko. Mi bomo pustili kar enico, ker tega elementa v seznamu ne bomo potrebovali.

Problem bomo razbili na dve funkciji:

• Funkcija, ki nam bo ustvarila seznam z ničlami in enicami ter bo s pomočjo funkcije stPoti vrnila število možnih poti:

  • pot(n)

• Rekurzivna funkcija, ki bo vrnila število možnih poti za dan seznam in pozicijo:

  • stPoti(sez, vr, st)

Naša funkcija bo sprejela parameter n. Tabela bo tako dimenzije n x n.
Kot smo že prej omenili, bo potem naš seznam dimenzije (n+1) x (n+1).

Čisto na začetku preverimo, če je podan n, res tipa int(če je res celo število) in, če je n večje od 0. Če pogoja ne držita, sprožimo napako.

• assert type(n)==int, 'Parameter n mora biti celo število, saj predstavlja dimenzijo tabele.'
• assert n>0, 'Vrednost parametra n mora biti večja ali enaka 0!.'

Nato preverimo, ali je n enak 1. Če je, vrnemo 2.

• Vemo, da je število poti v 1x1 veliki tabeli/kvadratu enako 2.

Če je n različen od nič ustvarimo seznam s samimi ničlami:

• Ustvarimo prazen seznam --> a=[]
• n=n+1

• Pomagamo si s for zanko, ki teče od 0 do n. Vsakič dodamo seznamu nov seznam dolžine n s samimi ničlami:

  • a.append([0]*n)

Sedaj imamo seznam s samimi ničlami.
Zadnji stolpec napolnimo z enicami. To naredimo tako, da gremo z enojno for zanko čez seznam. Vsakemu zadnjemu elementu i-te vrstice dodelimo vrednost 1.

• a[i][n-1]=1

Spremenimo samo še zadnjo vrstico. Do zadnje vrstice dostopamo s sez[n]:

• a[n-1] =n*[1]

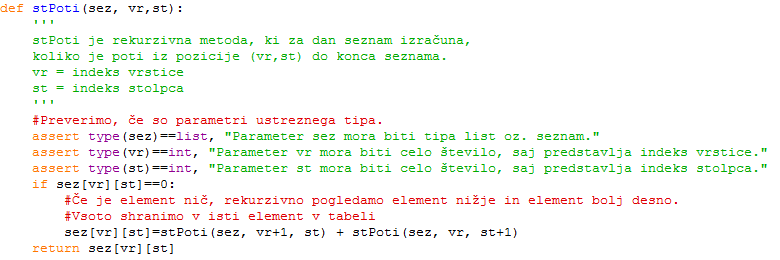
Funkcija bo vračala rezultat, ki ga bomo dobili s pomočjo klica funkcije stPoti(a, 0, 0).

• Število poti iz zgornjega levega kota (točka (0,0)) do spodnjega desnega kota (točka (n-1, n-1)) podanega seznama a nam bo izračunala rekurzivna funkcija stPoti(sez,vr,st).

Ta funkcija bo rekurzivno preverila koliko je možnih poti od podane lokacije (sez[vr][st]) do konca seznama oz. do lokacije sez[n-1][n-1].

Na začetku funkcije najprej preverimo, če so vsi parametri zahtevanega tipa.

• sez mora biti tipa list
• vr in st morata biti tipa int

Če so parametri drugačnih tipov, sprožimo napako. Pomagamo si s stavkom assert.

Nato najprej »pogledamo« kakšno vrednost ima element seznama podane lokacije (sez[vr][st]).

• Če je vrednost različna od nič, vemo, da je od te lokacije naprej točno toliko poti, kot je vrednost tega elementa.

• Če pa je element enak nič, seštejemo vrednost elementa pod nami in elementa desno od nas.

  • Poti/vrednost elementa pod nami dobimo z rekurzivnim klicem stPoti(sez, vr-1, st).
  • Poti/vrednost elementa desno od nas pa z rekurzivnim klicem stPoti(sez,vr, st+1).
• Dobljeno vsoto zapišemo v element sez[vr][st]

Vrnemo vrednost elementa sez[vr,st].

Možnih poti iz zgornjega levega kota do spodnjega desnega kota je 137846528820, če seveda ne dovoljujemo "hoje nazaj".

Python datoteka

Testne primere bomo pisali v svojo .py datoteko.
V to datoteko na začetku uvozimo funkcije iz datoteke Poti.py.

• import Poti

  Testni primeri:

  Preverimo, če deluje za n=1, n=2 in n=3. Pomagamo si z assert stavki. Če pogoj znotraj asserta ne bo držal, bo program sprožil napako, ki jo podamo v nizu.

• n=1… obstajata dve poti:

  • assert pot(1)==2, 'Napaka!'

• n=2… obstaja 6 poti:

  • assert pot(2)==6, 'Napaka!'

• n=3… obstaja 20 poti:

  • assert pot(3)==20, 'Napaka!'

Preverimo, če za napačen parameter sproži napako. Tukaj si bomo pomagali z varovalno mrežo try/except.

• Pričakujemo, da se bo sprožila napaka, če podamo parameter neustreznega tipa ali pa, če podamo parameter, katerega vrednost je manjša od 1.

try:
    pot('8')
    print('Sprožiti bi se morala napaka, a se ni!')
except:
    pass

try:
    pot(-1)
    print('Sprožiti bi se morala napaka, a se ni!')
except:
    pass