BINOMSKO DREVO

Da bi razumeli pojem binomske kopice, si najprej poglejmo kaj je binomsko drevo.
Binomsko drevo je rekurzivna podatkovna struktura. Mora veljati:

• binomsko drevo reda 0 je eno samo vozlišče
• najmanjši ključ (podatek) v drevesu se nahaja v korenu

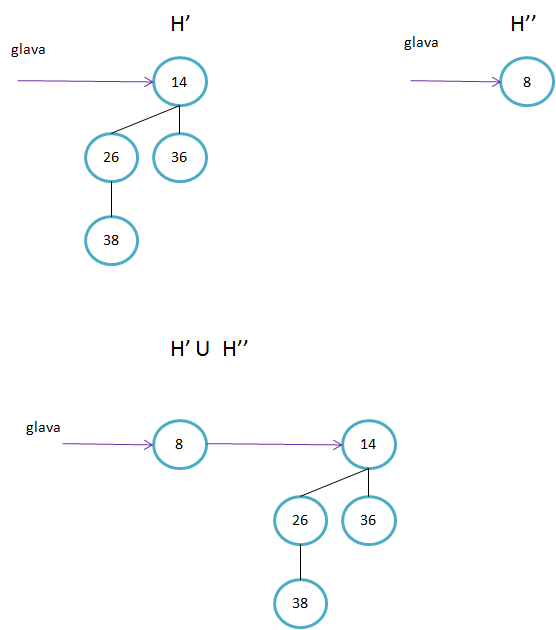
• binomsko drevo je sestavljeno iz dveh poddreves kjer velja:

  • manjši kjuč v korenu obeh poddreves, je tudi koren drevesa
  • binomsko drevo , ki je imelo večji ključ v korenu, pa postane levo poddrevo drevesa
    

V binomskem drevesu imamo elementov, višina drevesa pa je .

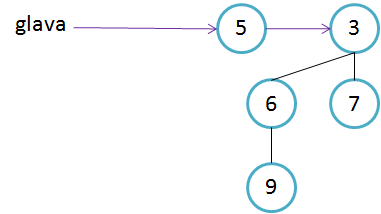
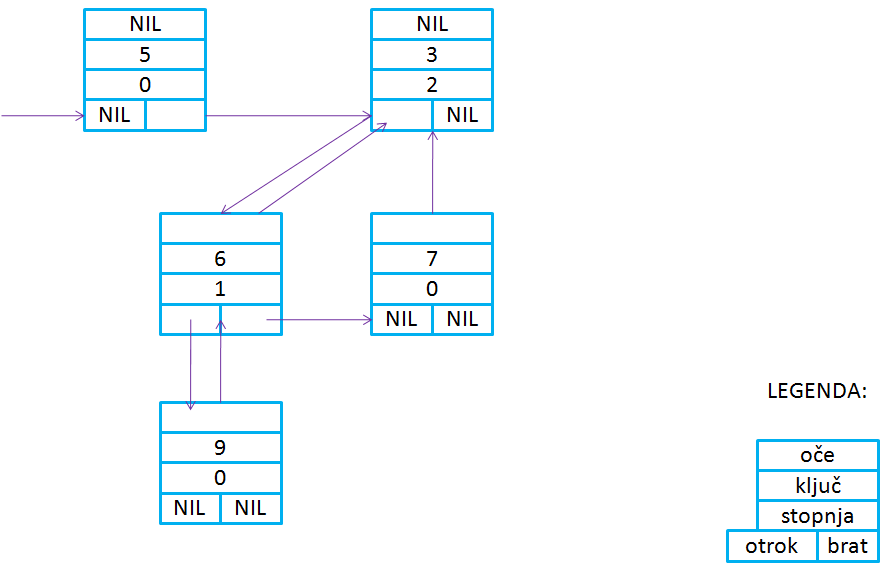
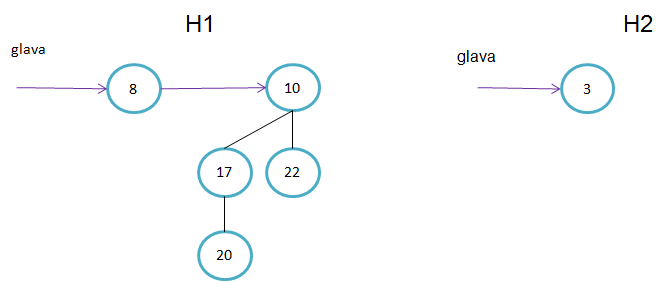
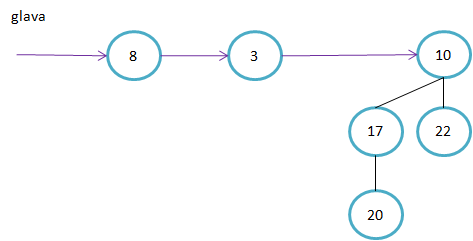
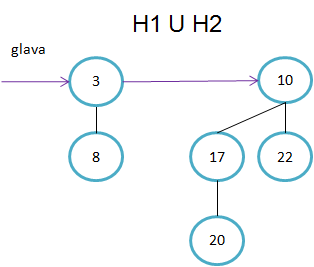
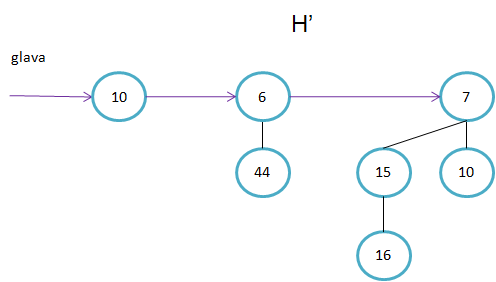
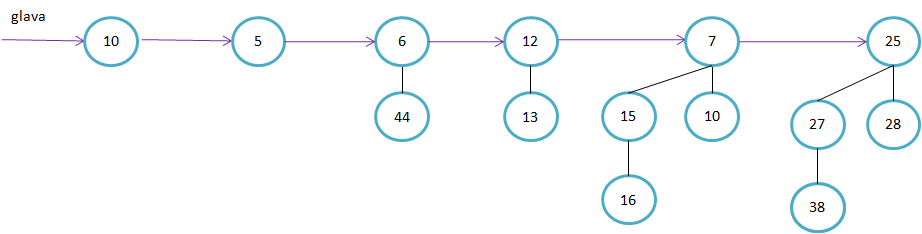
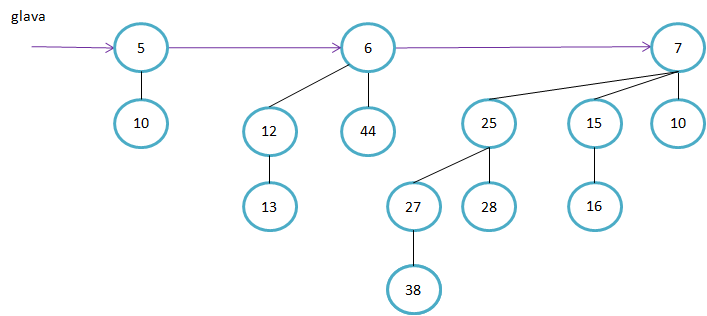
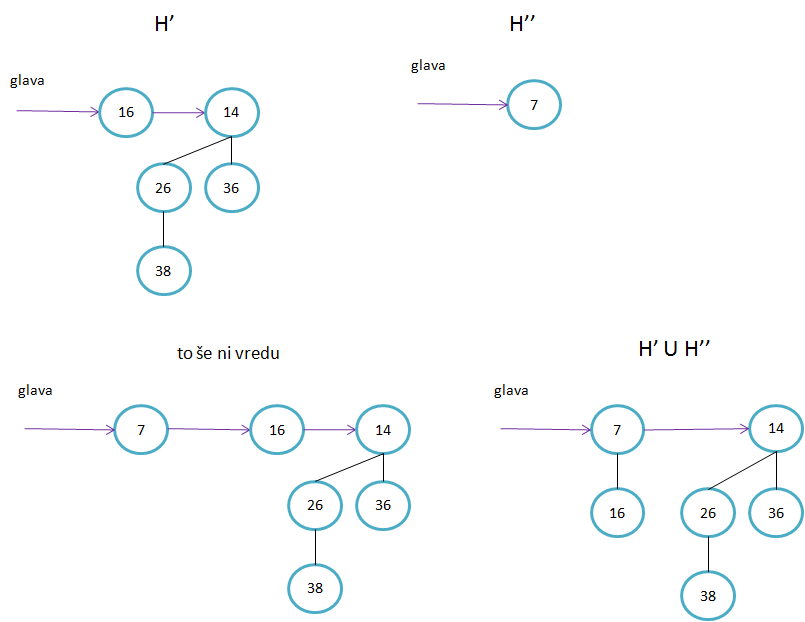
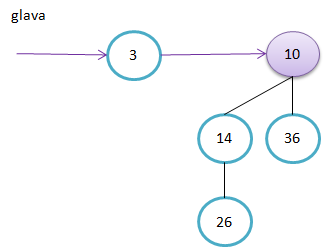
Primeri binomskih dreves:

Binomska drevesa

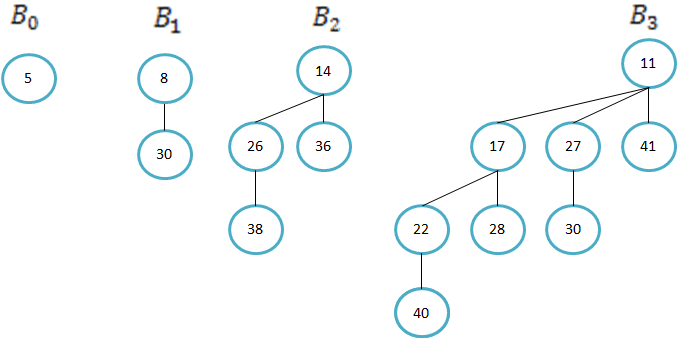
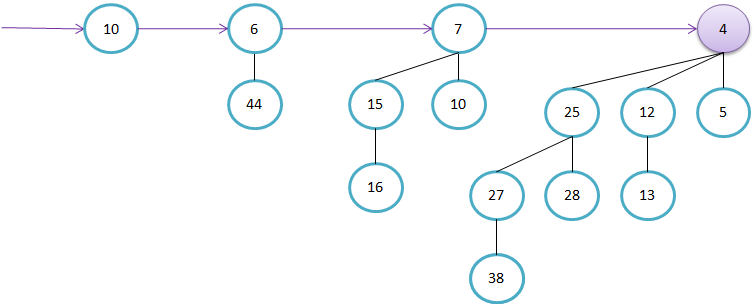
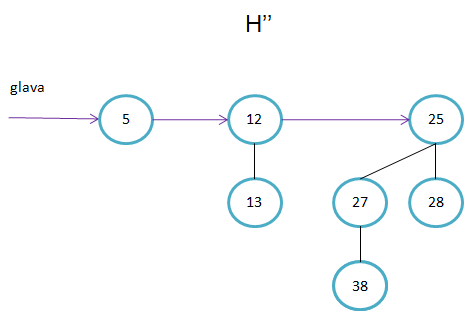
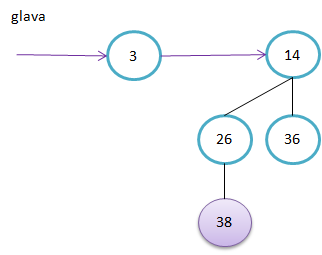
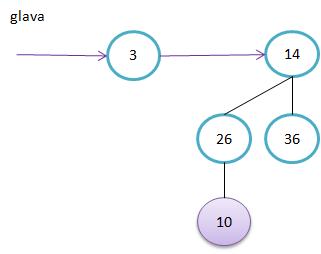
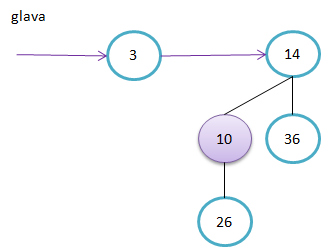
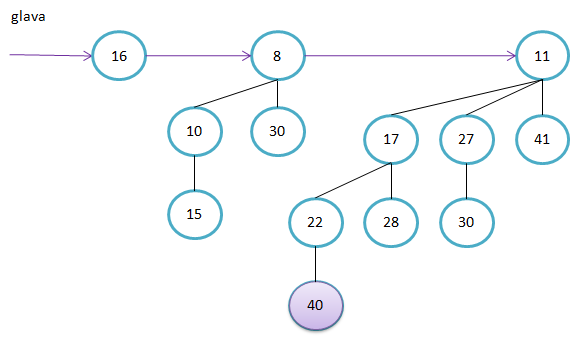
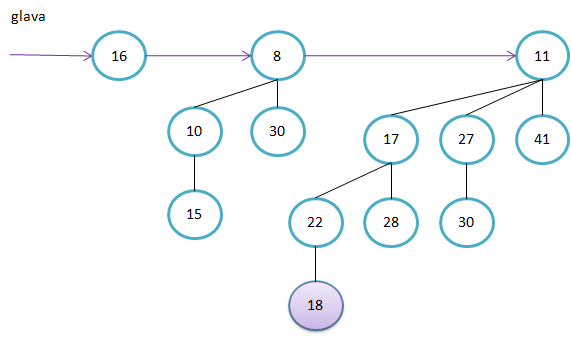
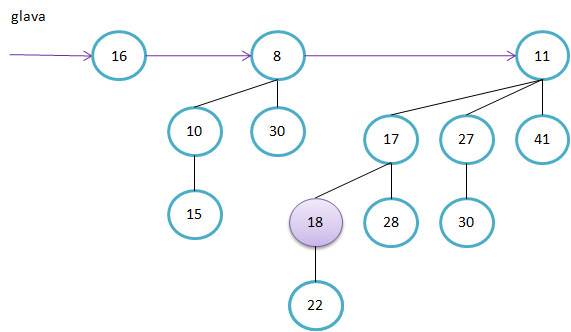
Primer kako sestavimo B4. Ključa v korenu poddreves B3 sta 11 in 19. Ker je 11<19, bo 11 tudi v korenu drevesa B4.

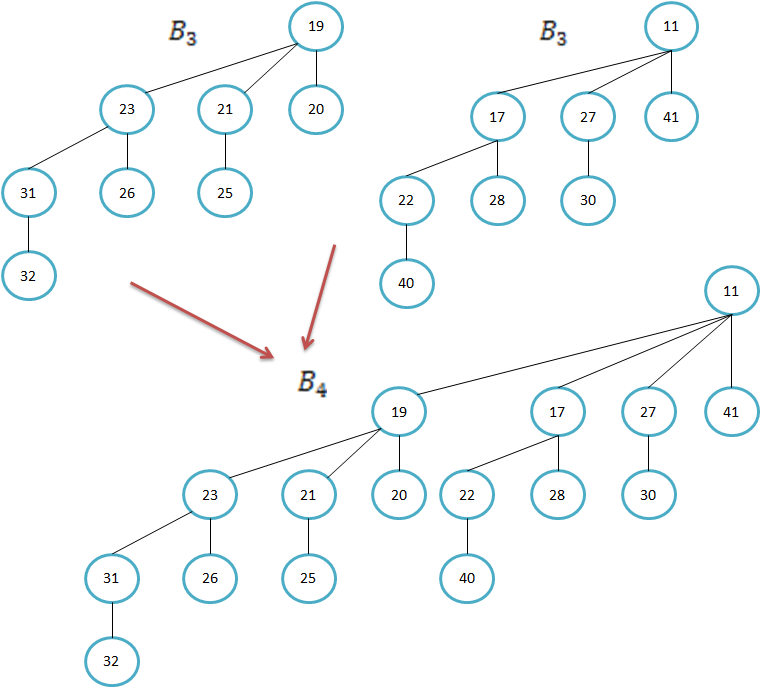
Binomska drevesa

BINOMSKA KOPICA

Binomska kopica je podatkovna struktura. Sestavljena je iz binomskih dreves, ki izpolnjujejo naslednje lastnosti:

• Vsako binomsko drevo v binomski kopici ima lastnost minimalnih kopic. Ključ vsakega vozlišča mora biti vedno večji ali enak ključu svojega starša. Iz tega sledi, da ima koren najmanjši ključ v binomskem drevesu.
• V binomski kopici obstaja kvečjemu eno binomsko drevo za vsak red, vključno z ničtim redom.
  

Binomska drevesa v binomski kopici so razvrščena naraščajoče glede na stopnje dreves.

Kako je število povezano z binomsko kopico?
Število predstavlja število vseh elementov binomske kopice.
Število lahko zapišemo v binarnem oz. dvojiškem zapisu.
Število dreves in njihov red je določeno s številom . Za lažjo predstavo bomo za izbrali število 10 ( v desetiškem zapisu). Pretvorimo v binarni zapis: = 1010.
Če pogledamo izraz . Ta izraz nam pove, da bomo imeli binomsko drevo reda 3 (eksponent nam določa stopnjo binomskega drevesa) z vozlišči. Izraz pa na pove, da ne bomo imeli drevesa stopnje 2, saj smo množili s številom 0. Torej končni rezultat je: binomska kopica je sestavljena iz binomskih dreves reda 3 in 1.

Osnovni način:

S tabelo :

UNIJA DVEH BINOMSKIH KOPIC

Imamo dve binomski kopici H1 in H2. Unija bo binomska kopica H. Dve binomski kopici združimo na sledeči način:

• Binomska drevesa iz H1 in H2 razvrstimo glede na stopnje oz. red dreves (od najmanjše stopnje do največje).
• Če H1 in H2 vsebujeta binomski drevesi reda , ju združimo v binomsko drevo H reda +1. Koren združenega binomskega drevesa, bo tisti izmed korenov iz H1 ali H2, ki je imel manjši ključ. Binomsko drevo z večjim ključem v korenu, pa postane levo poddrevo združenega binomskega drevesa H.
  Ker H1 ali H2 lahko vsebujeta binomsko drevo reda +1, ga bomo združili z H' na podoben način.
  Če H1 IN H2 vsebujeta binomsko drevo reda +1, združimo ti dve drevesi, H' pa pustimo pri miru.
• Postopek združevanja ponavljamo, dokler vsa binomska drevesa v združeni kopici niso različnih stopenj.
  
  
  

Primer unije :

1. korak:
Razvrstimo binomska drevesa iz H1 in H2 glede na stopnje dreves.

2. korak:
Prvo in drugo binomsko drevo sta istega reda, zato ju združimo. Koren združenega binomskega drevesa bo tisti izmed korenov obeh dreves, ki je imel manjši ključ. To je ključ 3. Drevo, ki edino vsebuje vozlišče s ključem 8, pa postane poddrevo združenega binomskega drevesa.

Ker nimamo več binomskih dreves enakih stopenj, je to končna rešitev.

BRISANJE VOZLIŠČA Z MINIMALNIM KLJUČEM

Iz binomske kopice želimo izbrisati najmanjši ključ (podatek) x. Kot vemo, se najmanjši ključ nahaja v korenu v enem izmed binomskih dreves, ki sestavljajo binomsko kopico.
Nato ustvarimo novo binomsko kopico H, ki bo vsebovala zaporedje poddreves (otrok) vozlišča z minimalnim ključem x v obratnem vrstnem redu kot prej ( torej na prvem mestu bo poddrevo z najnižjo stopnjo).
H pa naj bo prvotna binomska kopica, ki v zaporedju binomskih dreves, ne vsebuje binomskega drevesa, ki je vseboval minimalni ključ x.
V nadaljevanju združimo H in H s pomočjo operacije UNIJA DVEH BINOMSKIH KOPIC in dobimo novo binomsko kopico, ki ne vsebuje vozlišča x.

Primer :

1. korak:
Sedaj bomo ustvarili novo binomsko kopico H , ki bo vsebovala zaporedje poddreves (otrok) vozlišča s ključem 4, začenši s poddrevesom z najmanjšo stopnjo.

2. korak:
H pa naj bo prvotna binomska kopica, ki v zaporedju binomskih dreves, ne vsebuje binomskega drevesa, ki je vseboval vozlišče z minimalnim ključem 4.

3. korak:
H in H bomo združili s pomočjo operacije UNIJA DVEH BINOMSKIH DREVES. Prvo bomo binomska drevesa iz H in H razvrstili glede na stopnje dreves.

4. korak:
Kot vidimo imamo sedaj več binomskih dreves iste stopnje. Zato moramo drevesa iste stopnje združit s pomočjo operacije UNIJA DVEH BINOMSKIH DREVES.

Slika predstavlja končno rešitev.

VSTAVLJANJE NOVEGA VOZLIŠČA

• imamo podano binomsko kopico H
• ustvarimo novo binomsko kopico H, ki vsebuje novo vozlišče
• združimo H in H s pomočjo operacije UNIJA DVEH BINOMSKIH KOPIC

Primer 1:

Slika H in H predstavlja končno rešitev.

Primer 2:

Tretja slika še ni vredu, saj imamo dve binomski drevesi enake stopnje, zato ju moramo še združiti.
Slika H in H predstavlja končno rešitev.

ZMANJŠANJE KLJUČA VOZLIŠČA

Prvotni ključ nadomestimo z novim ključem (z manjšo vrednostjo). Ker hočemo ohraniti lastnost minimalne kopice, moramo pogledati očeta vozlišča z novim ključem. Če je ključ očeta manjši od novega ključa potem končamo. V nasprotnem primeru, vozlišče z novim ključem zamenjamo z vozliščem njegovega očeta. Postopek nadaljujemo, dokler je novi ključ večji od očetovega ali je novi ključ v korenu.

Primer 1:
Ključ 38 hočemo nadomestiti s ključem 10.

1. korak:
Ključ 38 nadomestimo z novim ključem 10.

2. korak:
Pogledamo ključ njegovega očeta. Ker je 26>10, vozlišči zamenjamo.

3. korak:
Pogledamo očeta vozlišča s ključem 10. Ker je 14>10, vozlišči zamenjamo.

Ker smo prišli do korena binomskega drevesa, postopek končamo.

Primer 2:
Ključ 40 hočemo nadomestiti s ključem 18.

1. korak:
Vozlišče s ključem 40 zamenjamo z novim ključem 18.

2. korak:
Pogledamo ključ očeta od vozlišča z novim ključem. Ker je ključ očeta 22, večji od novega ključa, vozlišči zamenjamo.

3. korak:
Pogledamo ključ očeta od vozlišča s ključem 18. Ker je 17<18, je lastnost minimalne kopice izpolnjena, zato je zgornja slika končna rešitev.

BRISANJE VOZLIŠČA

Zagotoviti moramo, da prvotna binomska kopica ( pred operacijo BRISANJE VOZLIŠČA) ne vsebuje ključa -. Ko hočemo določeno vozlišče izbrisati, vrednost njegovega ključa nadomestimo z -. S tem zagotovimo, da bo ta ključ minimalen v binomski kopici. Če je vozlišče s ključem - v korenu binomskega drevesa, vozlišče izbrišemo, kjer uporabimo operacijo BRISANJE MINIMALNEGA VOZLIŠČA. V nasprotnem primeru vozlišče s ključem - prepeljemo do korena (glej operacijo ZMANJŠANJE KLJUČA VOZLIŠČA) in ga nato odstranimo, kjer uporabimo operacijo BRISANJE MINIMALNEGA VOZLIŠČA.

Primer :

1. //www.cs.princeton.edu/~wayne/cs423/lectures/heaps-4up.pdf
2. //www.cs.rochester.edu/~gildea/csc282/slides/C19-binomial.pdf
3. //wiki.fmf.uni-lj.si/wiki/Binomska_kopica
4. //en.wikipedia.org/wiki/Binomial_heap
5. //wiki.fmf.uni-lj.si/wiki/Binomsko_drevo
   PowerPoint datoteki:

1. www.cs.unc.edu/~plaisted/comp750/05-binheaps.ppt
2. //www.google.com/search?q=Tan+Van+Binomial+Heap+Presentation+site:caveshadow.com

Ključne besede:
ključ - podatek