- Podano imamo množico .
- Množica ima točk. = .
- Vsaka točka ima dve koordinati - in .
Iščemo taka in , da bo razdalja najmanjša.

Predstavitev Seminarske naloge Iskanje najbližjega para točk
Opis problema
Enostaven algoritem
Enostaven algoritem je neposredni pristop za izračun najkrajše razdalje med točkama. Izračunamo razdaljo za vsak par točk in nato poiščemo najmanjšo.
Razdalja med točkama dobimo z
Analiza enostavnega algoritma
Osnovni operaciji pri enostavnem algoritmu sta:
- Izračun med dvema točkama
- Primerjava razdalj.
V primeru, ko imamo točk, se izvede izračunov razdalj in za eno manj primerjav razdalj.
Časovna zahtevnost takšnega algoritma je .
Zahtevnejši algoritem Deli in Vladaj
Z zahtevnejšim algoritmom lahko problem rešimo hitreje.
Algoritem deli in vladaj se deli na tri faze:
Faza DELI:
- Razdelimo problem na podprobleme.
Faza VLADAJ:
- Za vsako ravnino poišče par najbližjih točk.
Faza ZDRUŽITEV:
- Združimo rešitve vsakega podproblema.
- Ugotovimo, katera je najmanjša razdalja oz. par najbližjih točk.
Določiti moramo zaustavitvene pogoje za rekurzivni algoritem:
- Če : problem razdelitve nadaljujemo
- Če : izračunamo razdaljo med točkama in vrnemo razdaljo
- Če : izračunamo razdaljo med vsemi tremi točkami in vrnemo najkrajšo razdaljo
Faze Deli
Kadar je problem večji od 3, se ga lotimo z fazo DELI:
- Množico točk uredimo po -koordinati.
- Množico razdelimo na dve podmnožici in .
Pas, ki deli množico na dva dela je .
=> in => =
Primer:ima 6 točk. Meja je med točkama in
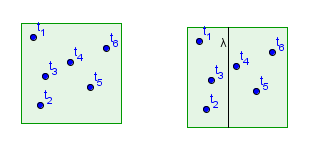
ima 7 točk Meja je med točkama in - se nahaja na razpolovišču njunih koordinat. Izračunamo jo: =
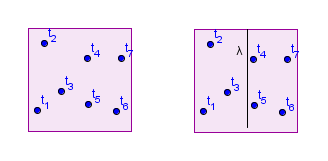
Faza Združitve
- Izračunamo najmanjšo razdajo med in .
- Pogledati je treba, če obstaja kakšna manjša razdalja med točkama iz in (ena točka leži v , ena pa leži v ) kot dobljena razdalja .
- Dobljeno razdaljo odmerimo od ločilne črte v levi in desni pas. V čezmejnem pasu poiščemo najkrajšo razdaljo in jo primerjamo z razdaljo .
- Točke razvrstimo po -koordinatah in nato po -koordinatah. Za to uporabimo metodo urejanje.
Točke v sredinskem pasu
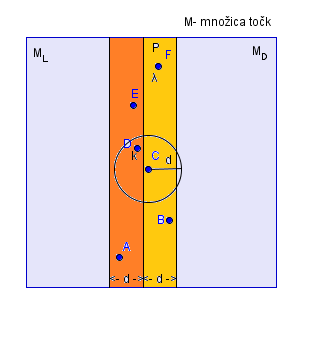
Pogledamo ostale možne razdalje:
- Za vsak par točko v pasu izračunamo razdalje.
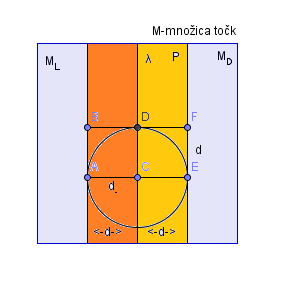
- Razporedimo točke v pasu P po - smeri kot na sliki.
- Izberemo na primer točko C ( najbolj skrajna točka) in preverimo, ali je kakšna točka oddaljena za manj kot .
Če bi imeli več točk v območju točke C:
- Na primer, po tri točke imajo isto koordinato.
- Z omejitvijo po koordinati dobimo območje pravokotnika.
- V kvadratu lahko na vsaki strani ležijo največ 4 točke, skupno 6 točk.
Za vsako točko preverimo razdaljo zgolj do petih nadaljnjih točk v seznamu.
Analiza algoritma deli in vladaj
Zapis iskanja najbližjega para točk smo poenostavili na iskanje razdalje med najbližjima točkama. V samem algoritmu pa moramo poskrbeti, da se zabeležita in vrneta točki, ki pripadata najmanjši razdalji.
Celotni algoritem ima časovno zahtevnost = , kar je boljše od .
Algoritem lahko še izboljšamo s pomočjo algoritma urejanje z zlivanjem.
Fazo združevanja dominirajo tri podfaze s časovno zahtevnostjo . Vseh rekurzivnih nivojev je , časovna zahtevnost algoritma je .