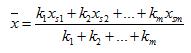Vir :

Splošna matura - junij 2004 - osnovna raven - 6. naloga

povezava do naloge

Besedilo naloge :

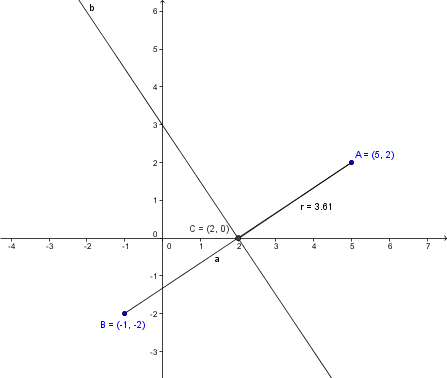
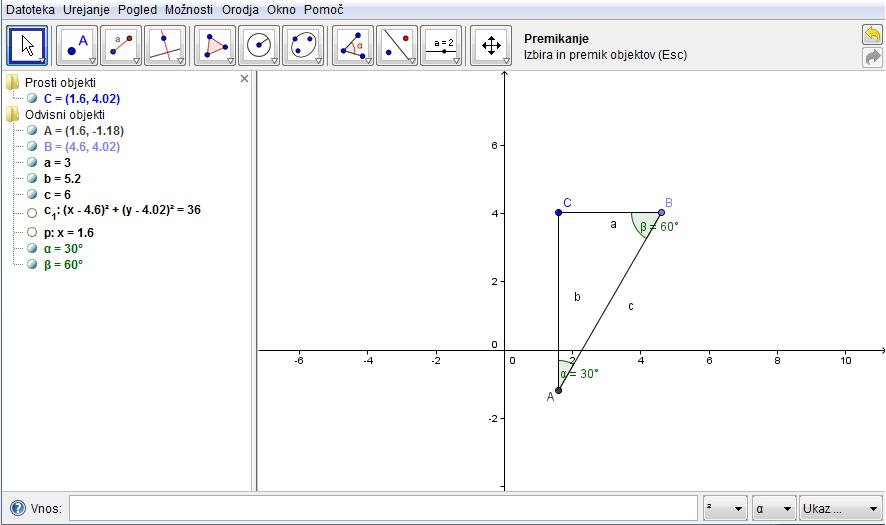
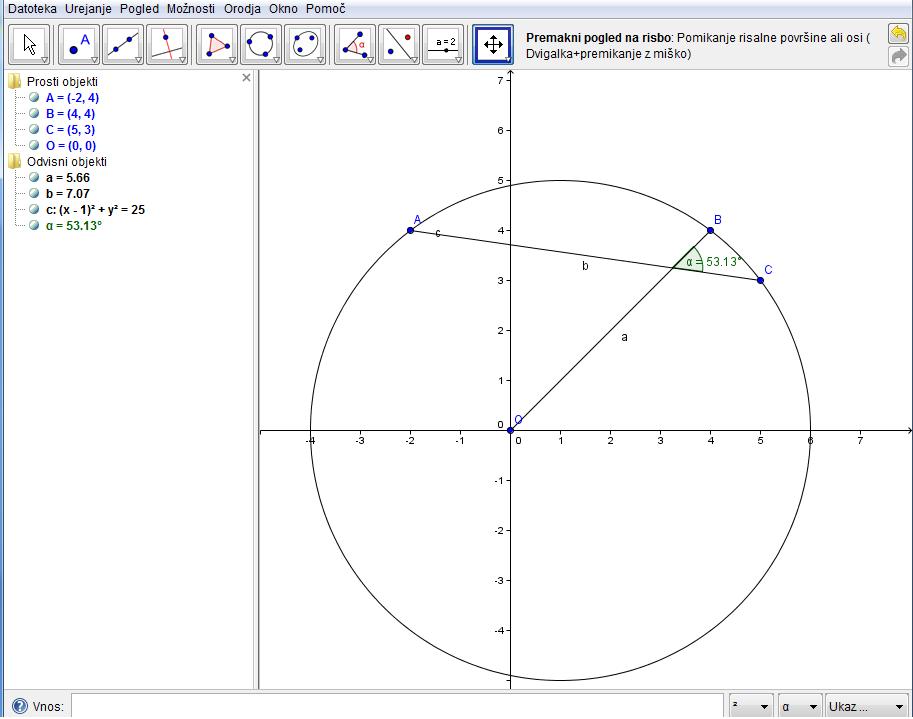
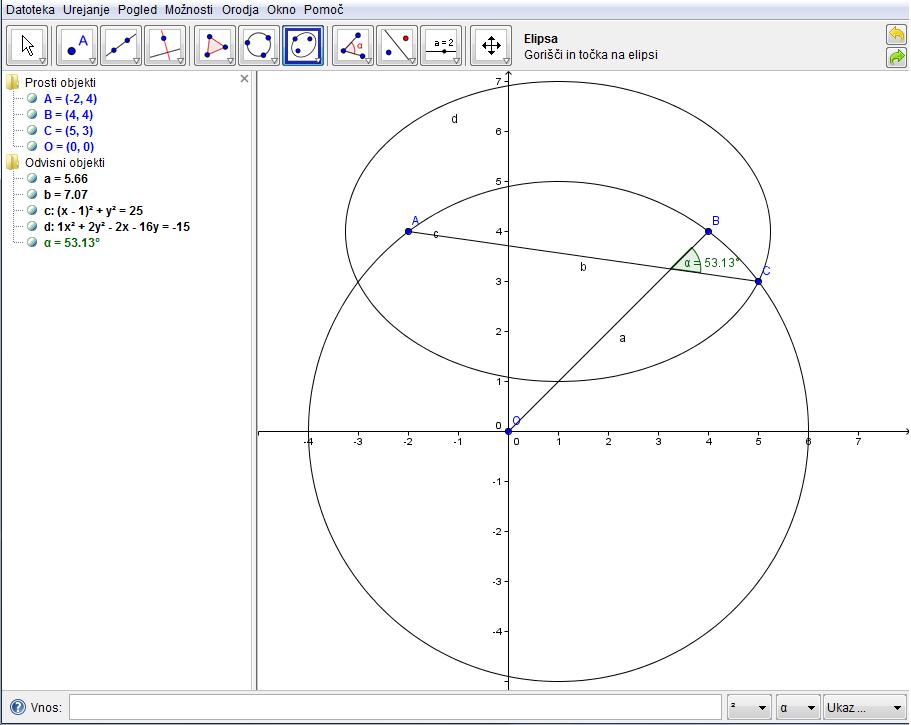
Točki A ( 5, 2) in B( -1, -2) sta krajišči enega od premerov krožnice. Izračunajte središče in polmer te krožnice ter zapišite njeno enačbo.

Matematično ozadje :

Razdalja med točko A in B je premer krožnice. Torej polmer izračunamo tako, da izračunamo to razdaljo med točkama in delimo z 2. Enačba krožnice z središčem S ( p, q ) in polmerom r je (x – p )^2 + (y – q )^2 = r^2 . Iz te enačbe potem izračunamo koordinate središča.

Postopek reševanja v GeoGebri:

• V ukazno okno vnesemo ukaz za točko A in B :

  • A = (5, 2 )
  • B = (-1, -2 )
• Narišemo daljico a skozi točki A in B, s pomočjo ikone Daljica med dvema točkama ali pa z ukazom daljica[A,B].
• Nato to daljico a razpolovimo na dva enaka dela z simetralo daljice (premica b) preko ikone ali pa z ukazom simetralaDaljice[a].
• Z točko C označimo presečišče daljice a in simetrale. Točka C je središče krožnice in njene koordinate odčitamo iz seznama objektov oz. ji na risalni površini dodamo poleg imena tudi vrednost ( C= (2, 0) ).
• V ukazno okno vnesemo ukaz : r = daljica[C,A] . Tako dobimo naš iskani polmer, njegovo dolžino odčitamo iz seznama objektov oz. mu na risalni površini dodamo poleg imena tudi vrednost ( r = 3.61).

Enačba krožnice je torej : (x - 2)^2 + y^2 = 3.612

Vir :

Splošna matura - junij 2004 - osnovna raven - 11. naloga

povezava do naloge

Besedilo naloge :

Izračunajte kot, pod katerim graf funkcije f(x) = (x-2) / x seka abscisno os. Kot zapišite na stotinko stopinje natančno.

Matematično ozadje :

Potrebno si je funkcijo približno narisati in poiskati ničlo oz. točko kjer seka x os ali pa jo izračunati. Določiti še moramo tangento na funkcijo skozi ničlo. Potem pa se kot med funkcijo in x –osjo izračuna po formuli :

Postopek reševanja v GeoGebri:

• V ukazno okno vnesemo ukaz : f(x) = (x-2)/x.
• Potem določimo točko, kjer funkcija f(x) seka x-os (A = (2,0)).
• V ukazno okno še vnesemo x-os (v našem primeru premica b) : y = 0
• Narišemo tangento c skozi točko A glede na našo funkcijo. To lahko naredimo preko ikone Tangente ( izberemo točko A in potem našo funkcijo) ali pa preko ukaza tangenta[A, f(x)].
• Nato pa z ikono Kot označimo manjši kot med x-osjo (premico b) in tangento c in odčitamo pod katerim kotom funkcija seka x os (α = 26.57°).

Vir :

Splošna matura – 6. junij 2005 - osnovna raven - 8. naloga

povezava do naloge

Besedilo naloge :

V pravokotnem koordinatnem sistemu so dane točke A( 2, 1), B(-2, 3) in C( 3, -2). Zapišite vektorja AB in AC s komponentami, izračunajte njun skalarni produkt in kot, ki ga oklepata.

Matematično ozadje :

Če imamo podani dve točki A (a1, a2) in B (b1, b2), so komponente vektorja AB = (b1 – a1, b2 - a2). Skalarni produkt dveh vektorjev je nek skalar.

Če imamo vektor u = (u1, u2) in vektor v = (v1, v2) je njun skalarni produkt (u*v) = u1*v1 + u2*v2. Z formulo, kjer sta u in v vektorja, |u| in |v| pa njuni dolžini : u*v = |u| * |v| * cosφ lahko izračunamo kot, ki ga oklepata.

|u| = (u1^2 + u2^2)1/2

Postopek reševanja :

v GeoGebri :

• V ukazno okno vnesemo točke :

  • A ( 2, 1 )
  • B ( -2, 3 )
  • C ( 3, -2 )

• Potem narišemo vektor z začetno in končno točko :

  • Vektor AB ( z začetno točko v A in končno v B) = u
  • Vektor AC ( z začetno točko v A in končno v C) = v

• Iz seznama objektov odčitamo komponente vektorjev:

  • u = ( -4, 2 )
  • v = ( 1, -3 )
• Skalarni produkt izračunamo tako, da v ukazno okno vpišemo : u*v (-10).
• Označimo kot med vektorjema u in v z ikono Kot in odčitamo njegovo vrednost ( α = 135°).

v Matlab-u :

• Tukaj izračunamo skalarni produkt v*u . Vektor v pišemo kot vrstični vektor, u pa kot stolpčni vektor. Če pa pišemo oba v stolpčni obliki pa je skalarni produkt sum(u.*v) Rezultat je -10.

Vir :

Splošna matura – 6. junij 2005 - osnovna raven - 5. naloga

povezava do naloge

Besedilo naloge :

Gobar ima v košari lisičke, jurčke in sirovke. Tri četrtine števila vseh gob je lisičk, dvajset odstotkov je jurčkov, sirovki pa sta dve. Koliko gob ima gobar v košari?

Matematično ozadje :

Nastavimo si enačbo x = ¾ *x + x/5 +2

Postopek reševanja v WolframAlpha :

• Vnesemo : Solve [ x = 3/4 *x + x /5 + 2, x] ; In dobimo rezultat 40.

Vir :

Splošna matura – 6. junij 2005 - osnovna raven - 2. naloga

povezava do naloge

Besedilo naloge :

V pravokotnem trikotniku ABC (pravi kot je pri oglišču C ) merita stranici a = 3 cm in c = 6 cm . Natančno izračunajte dolžino stranice b in velikosti kotov α in β . Narišite skico.

Matematično ozadje :

Uporabimo pitagorov izrek za izračun dolžine b ( b = (c^2 – a^2 ) 1/2). Za računanje kotov pa uporabimo kotne funkcije v pravokotnem trikotniku (sin α = nasprotna kateta / hipotenuza).

Postopek reševanja v Matlabu:

• Definiramo c = 6 in a = 3 ter vnesemo enačbo b = sqrt(c^2 - a^2).

V Matlab-u še naloge nismo rešili do konca, ker še nimamo izračunanih kotov, zato uporabimo GeoGebro.

Postopek reševanja v Geogebri:

• Narišemo točko C, nato preko ikone daljico a z dano dolžino (3)od izbrane točke. Drugo točko te daljice preimenujemo v točko B.
• Narišemo pravokotnico na a skozi C preko ikone ali z ukazom Pravokotnica[C,a].
• Potem narišemo krožnico z središčem v točki B in polmerom 6 ( dolžina stranice c). Tam kjer se pravokotnica in krožnica sekata določimo točko A.
• Odstranimo pravokotnico in krožnico(odstranimo možnost prikaz objekta)ter dodamo daljico b (med točkama C in A) in odčitamo njeno dolžino (5.2).
• Označimo še kota α in β preko ikone Kot ter odčitamo njuni vrednosti ( α = 30°, β = 60°).

Vir :

Izpitna pola, poklicna matura-maj 2004, 2.del: 3. naloga

povezava do naloge

Besedilo naloge :

Pred vpisom v šolo so izmerili telesno višino 32 deklic. Dobili so vrednosti (v centimetrih, urejene po velikosti): 103, 104, 105, 106, 106, 107, 109, 110, 111, 111, 111, 112, 113, 113, 114, 114, 114, 115, 115, 116, 116, 117, 117, 117, 118, 118, 118, 120, 120, 121, 122, 122.

• a) Podatke uredite v 5 frekvenčnih razredov širine 4 cm.
• b) Iz grupiranih podatkov izračunajte povprečno višino deklic.
• c) Podatke prikažite s frekvenčnim poligonom, ali histogramom, ali kolačem.

Matematično ozadje :

Podatke grupiramo v 5 skupin širine 4 , npr 103 – 106, 107 – 110, 111- 114, … Potem uporabimo formulo za računanje povprečja v grupiranih podatkih :

kjer so k1, … , kn vrednosti, k1, …, kn pa frekvence. Narišemo še histogram.

Postopek reševanja v Excelu:

• Najprej vpišemo podatke, potem si jih razdelimo v 5 razredov z širino 4.
• Izračunamo si sredino posameznega razreda .
• Izračunamo frekvenco ( število deklic v skupini)posameznega razreda :

• Izračunamo število vseh deklic (uporabimo ukaz sum).
• Izračunamo si : sredina razreda*število deklic in potem te produkte seštejemo in delimo z število vseh deklic in tako dobimo povprečno višino.

• Narišemo še tortni in stolpčni grafikon, tako da označimo razrede in število deklic v teh razredih.

Vir :

Splošna matura – spomladanski rok, 1.junij 2006- osnovna raven – 11. naloga

povezava do naloge

Besedilo naloge :

Dana sta vektorja a = (2, -1, 3) in b = (1, -2, 5). Izračunajte njun skalarni produkt. Izračunajte vektor x = 2a – b. Izračunajte točno vrednost dolžine vektorja x.

Matematično ozadje :

Če imamo vektor u = (u1, u2, u3) in vektor v = (v1, v2, v3) je njun skalarni produkt (u*v) = u1*v1 + u2*v2+ u3*v3. Vektorje seštevamo in odštevamo po komponentah.

Dolžina vektorja u : |u| = ( u1^2 + u2^2 + u3^2 )1/2

Postopek reševanja v Matlabu:

• Definiramo :

  • a=[2;-1;3]
  • b=[1;-2;5]

• Izračunamo skalarni produkt :

  • skalarniprodukt = sum(a.*b)

• Izračunamo komponente vektorja x :

  • x = 2.*a – b

• Izračunamo še približno dolžino vektorja x :

  • dolzinax = sqrt(sum(x.^2))
  • sum(x.^2): (10)

Točna vrednost dolžine je torej 10^(1/2)

Vir :

Splošna matura – spomladanski rok, 1.junij 2006- višja raven - 2. pola – 1. naloga

povezava do naloge

Besedilo naloge :

V pravokotnem koordinatnem sistemu v ravnini so dane točke A ( - 2, 4 ), B (4, 4) in C(5, 3).

• a) Izračunajte kot med daljicama OB in AC . (Točka O je izhodišče koordinatnega sistema.) Rezultat zaokrožite na kotno minuto.
• b) Zapišite enačbo krožnice, ki poteka skozi točke A, B in C . Koliko meri polmer te krožnice?
• c) Zapišite enačbo tiste elipse z goriščema A in B , ki poteka skozi točko C . Elipso narišite v koordinatni sistem.

Matematično ozadje :

Izračunamo smerna koeficienta nosilki daljic in potem po formule za računanje kota med premicama določimo kot med daljicama. Iz enačbe krožnice (x – p )2 + (y – q )2 = r2 določimo koordinate središča in polmer.

Enačba elipse : (x – p )2 / a2 + (y – q )2 / b2 =1 , kjer sta a in b polosi, p in q pa koordinati središča.

Postopek reševanja v Geogebri:

• V ukazno okno vnesemo ukaz za štiri točke :

  • A = (-2, 4)
  • B = (4, 4)
  • C = (5, 3)
  • O = (0, 0)
• Potem narišemo daljici 0B in AC ter označimo preko ikone Kot, kot med njima (53.13°, kar je 53° 8' ). Torej 0.13 * 60 = 7.8 in zaokrožimo na 8. (1° = 60 ' )

• Narišemo krožnico skozi tri točke in iz seznama objektov odčitamo njeno enačbo:

  • (x - 1)2 + y2 = 25; Torej r2 = 25, kar pomeni, da polmer r meri 5.

• Narišemo elipso z goriščema A in B skozi točko C. In iz seznama objektov odčitamo njeno enačbo :

  • 1*x^2 + 2*y^2 – 2*x – 16*y = -15 .