Poišči vse rešitve sistema linearnih enačb:

• x-2y+z=1
• x-2y-t=-1
• 2x+4y+z-t=0
• -x+2y+z+2t=3.

RANK MATRIKE

Najprej sem preverila, če je sistem rešljiv. To sem storila tako, da sem preverila rank matrike A tvorjene iz koeficijentov pri neznankah in rank razširjene matrike sistema .

Slika v Matlab-u:

Kot je razvidno iz slike lahko vidimo, da se ranka ujemata, kar pomeni, da lahko nadaljujemo z reševanjem. Ker je rank matrike 3, število spremenljivk pa 4, pomeni, da bo ena od neznank parameter.

Razširjena matrika:

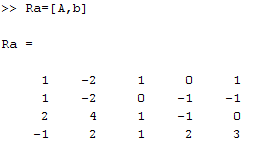
Drugi vrstici sem odštela prvo vrstico ter tretji vrstici sem odštela prvo vrstico pomnoženo z dva:

Četrti vrstici sem prištela prvo vrstico, nato sem še četrti vrstici prištela drugo vrstico pomnoženo z dva:

Tretji vrstici sem odštela drugo vrstico, nato sem še tretjo vrstico delila z osem:

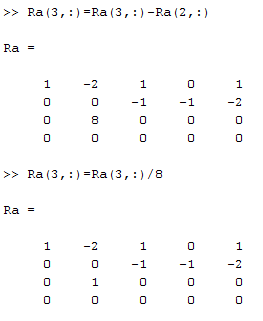
Drugo vrstico sem delila z minus ena, nato sem še prvi vrstici prištela tretjo vrstico:

Ob zamenjavi 2. in 3. vrstice sem dobila matriko:

Iz te matrike je razvidno, da je t parameter, z = 2 − t, y = 0 in x = t − 1.