Dana je funkcija
a)Določite ničle, pole, asimptote in ekstreme funkcije.
b)Narišite graf funkcije
c)Določite presečišči grafa funkcije s premico . Kolikšna je razdalja med presečiščema?
Besedilo naloge
Dana je funkcija
a)Določite ničle, pole, asimptote in ekstreme funkcije.
b)Narišite graf funkcije
c)Določite presečišči grafa funkcije s premico . Kolikšna je razdalja med presečiščema?
Reševanje naloge brez programa a)
a)
Ničla:
Pol: (pol je sode stopnje, zato ne zamenja predznaka)
Asimptota:
Ekstremi:
izračunamo odvod funkcije:
stacionarna točka:
predznak okoli stacionarne točke nam pove, da je ta točka maksimum
Dobili smo maksimum funkcije .
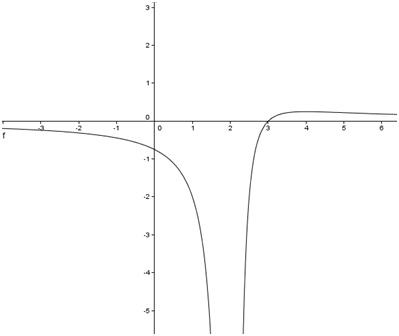
Reševanje naloge brez programa b)
b)
Reševanje naloge brez programa c)
c)
Presečišči grafa funkcije s premico sta:
Razdalja med presečiščema:
Reševanje naloge s programom GeoGebra in WolframAlpha
V vnosno okence vnesemo funkcijo
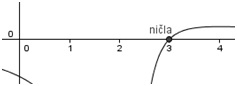
Ničle
Ničle funkcije dobimo s pomočjo gumba Presečišče dveh objektov.

Na sliki označimo graf funkcije in abscisno os. Vidimo, da je ničla funkcije v točki . To točko preimenujemo v ničla, da je na grafu bolj razvidna.
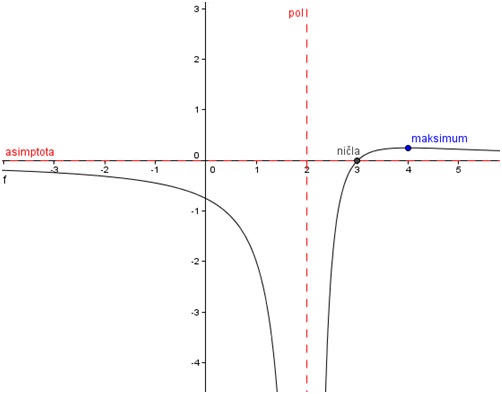
Pol in Asimptota
Pole in asimptote funkcije dobimo s pomočjo programa WolframAlpha in sicer tako, da v vnosno okence vpišemo asymptotes (x-3)/(x-2)^2.
Dobimo pol

Dobimo asimptoto

Sedaj lahko pol in asimptoto vnesemo v GeoGebro
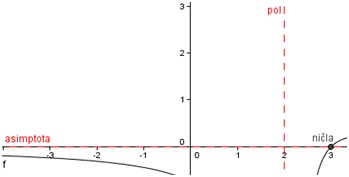
Ekstremi
Ekstreme dobimo s pomočjo programa WolframAlpha, kjer v okence vnesemo (x-3)/(x-2)^2.
Dobimo globalni maksimum v točki

Sedaj lahko maksimum vstavimo v GeoGebro
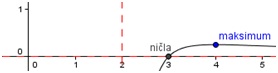
Sedaj graf funkcije zgleda takole:
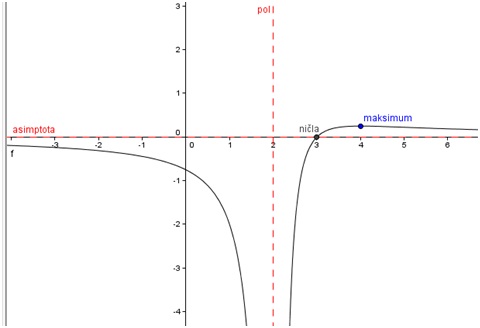
Presečišče
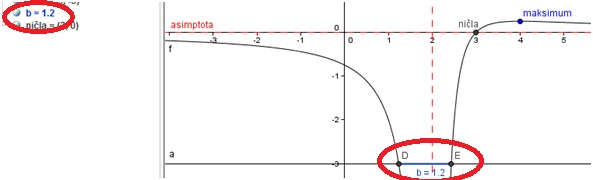
Presečišči grafa funkcije s premico dobimo tako, da najprej vstavimo v GeoGebro premico
Nato pa s pomočjo gumba Presečišče dveh objektov

označim graf in premico.
Dobimo presečišči v točkah
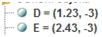
Razdaljo med presečiščema ugotovimo tako, da med točkama D in E naredimo daljico
Tako smo ugotovili, da je razdalja med presečiščema .