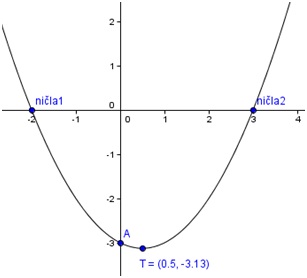
Kvadratna funkcija ima ničli -2 in 3. Njen graf seka ordinatno os v točki A(0, -3). Zapišite enačbo kvadratne funkcije, izračunajte koordinati temena in narišite njen graf.
5. naloga: kvadratna funkcija
Besedilo naloge
Reševanje naloge brez programa
Enačba kvadratne funkcije : f(x)=a(x+2)(x-3)
Vemo, da je f(0)=-3, zato lahko izračunamo a:
-3=a(0+2)(0-3)
-3=a(-6)
a=(-3)/(-6)
a=1/2
Zapis enačbe:
f(x)=1/2 (x+2)(x-3)
f(x)=1/2(x^2-x-6)
f(x)=1/2 x^2-1/2 x-3
Teme T=(p,q)
p=-b/2a=-(-1/2)/(2 1/2)=1/2
q=(4ac-b^2)/4a=(4 1/2 (-3)-1/4)/(4 1/2)=(-6-1/4)/2=((-24-1)/4)/2=((-25)/4)/2=-25/8
Koordinate temena so torej: T=(1/2,-25/8)
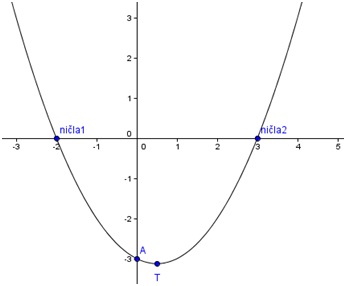
Reševanje naloge s programom GeoGebra in WolframAlpha
Najprej v GeoGebro vstavimo ničli funkcije in točko A
- (-2,0) (preimenujemo jo v ničla1)
- (3,0) (preimenujemo jo v ničla2)
- A=(0,-3)
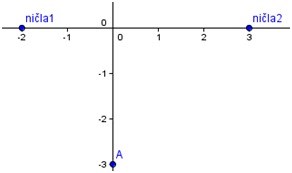
Reševanje naloge s programom GeoGebra in WolframAlpha (enačba)
Da dobimo enačbo funkcije, v vnosno okence vpišemo ukaz za polinom
- Polinom[ničla1, ničla2, A]
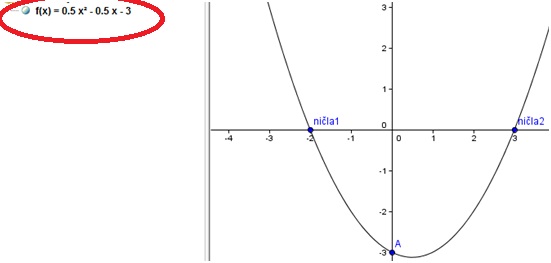
Reševanje naloge s programom GeoGebra in WolframAlpha (teme)
V WolframAlpha vpišemo (1/2)x^2-(1/2)x-3, da dobimo koordinate globalnega minimuma, ki je teme funkcije.

Sedaj v GeoGebro vnesemo teme funkcije
- T=(1/2, -25/8) (prikaz opisa nastavimo na ime&vrednost)