Osnovnica c enakokrakega trikotnika ABC meri 3√3, kot ob osnovnici pa 30°. Izračunajte kot γ pri vrhu C in natančno dolžino kraka a. Narišite skico.
7. naloga: Izračun kota pri vrhu C in dolžino kraka a v enakokrakem trikotniku
Besedilo naloge
Reševanje naloge brez programa
Vsota notranjih kotov trikotnika je 180°.
Enakokraki trikotnik ima kota α in β (kota ob osnovnici) enako velika.
α=30°
β=30°
180°-30°-30°=120°=> γ=120°
Formula: c^2=3a^2
(3√3)^2=3a^2
9∙3=3a^2
a^2=(9∙3)/3
dolžina kraka: a=3
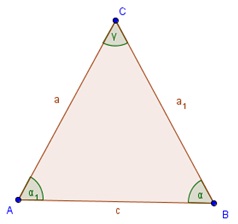
|
Reševanje naloge s programom GeoGebra
Vstavimo točko A
- A=(0,0)
Točko B in stranico c dobimo tako, da z gumbom Daljica z dano dolžino od izbrane točke

označimo točko A. Odpre se nam okno, kjer vpišemo dolžino daljice-stranice 3sqrt(3).
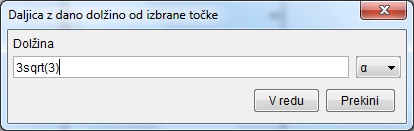
To daljico preimenujemo v c.

Reševanje naloge s programom GeoGebra
Kota α in β naredimo s pomočjo gumba Kot z dano velikostjo

Vemo da sta v enakokrakem trikotniku enaka.
Označimo točki A in B, v okence vpišemo kot 30° in označimo Negativna stran. Dobimo točko A'.

Označimo točki B in A, v okence vpišemo kot 30° in označimo Pozitivna stran. Dobimo točko B'.
Naredimo premico b skozi točki B, A' in premico c1 skozi točki A, B'
- Premica[B, A']
- Premica[A', B]
Reševanje naloge s programom GeoGebra
Točko C dobimo s pomočjo gumba Presečišče dveh objektov

.Označimo premici b in c1.
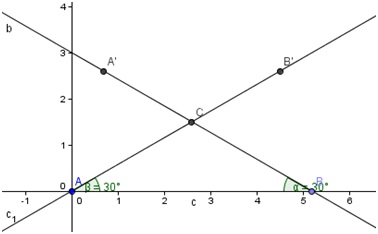
Reševanje naloge s programom GeoGebra
Naredimo trikotnik ABC
- Mnogokotnik[A, B, C]
Stranicam-daljicam c2, a in b1 nastavimo prikaz opisa na ime in vrednost. Tako ugotovimo, da stranici a in b1 merita 3 enote.
Kot γ dobimo s pomočjo gumba Kot
Označimo daljici-stranici b1, a in dobimo rezultat γ=120°.
Nazadnje še malo polepšamo (skrijemo premice, točki A', B'), da se bolje vidi.





