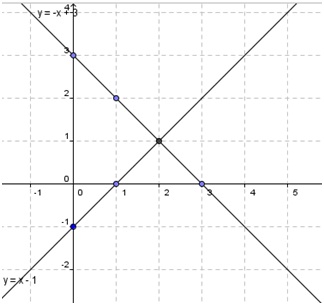
Narišite premici y=x-1 in y=-x+3. Izračunajte ploščino trikotnika, ki ga premici oklepata z abscisno osjo.

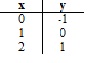
Točke y=x-1:

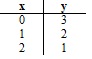
Točke y=-x+3:

skica

Opazimo, da je trikotnik enakokrak. Zato za ploščino uporabimo formulo S=(c∙v)/2.

v=1

c=2

S=(2∙1)/2=1

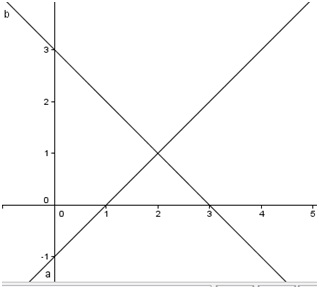
Premici vstavimo v GeoGebro in dobimo premici a in b

• y = x – 1
• y = -x + 3

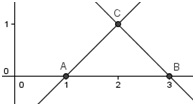
S pomočjo gumba Presečišče dveh objektov

naredimo točke trikotnika. Za točko A označimo abscisno os in premico a, za točko B označimo premico b in abscisno os, za točko C pa označimo premici a in b.

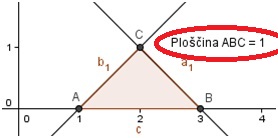
Ker želimo dobiti ploščino trikotnika, moramo narediti trikotnik (vnesemo ukaz)

• Mnogokotnik[A,B,C]

Označimo gumb Ploščina

in kliknemo na narisan trikotnik. Tako se nam je pregledno izpisala ploščina trikotnika.