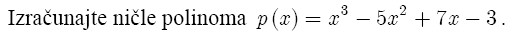
Matematična naloga
Besedilo naloge
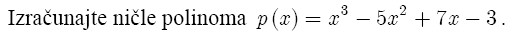
Potek reševanja
Nalogo bom rešila s programom Geogebra.
• V ukazno okno v Geogebro vpišemo naš dan polinom na ta način: p(x)=x^3-5*x^2+7*x-3.
• Po kliku Enter, nam program nariše dan polinom.
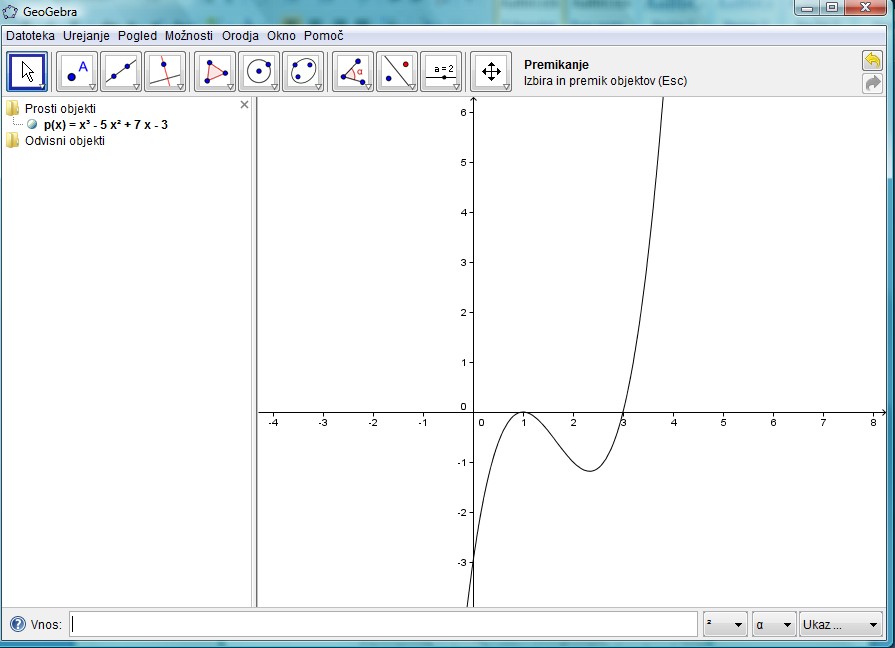
• Nato, da bomo dobili ničle polinoma vpišemo ukaz Ničla[p(x)]. V ukaz med oglatima oklepajema smo vnesli p(x), saj želimo dobiti ničle polinoma, katerega smo na začetku označili s p(x). Lahko bi tudi v oglata oklepaja vpisali kar cel polinom in bi dobili enako.
• Sedaj dobimo za ničli dve točki in sicer točki A in B, kateri se nahajata na abscisni osi, ter zanju dobimo rezultat A=(1,0) in B=(3,0), ki nam ju je izpisalo tudi na levo stran pod Odvisni objekti.
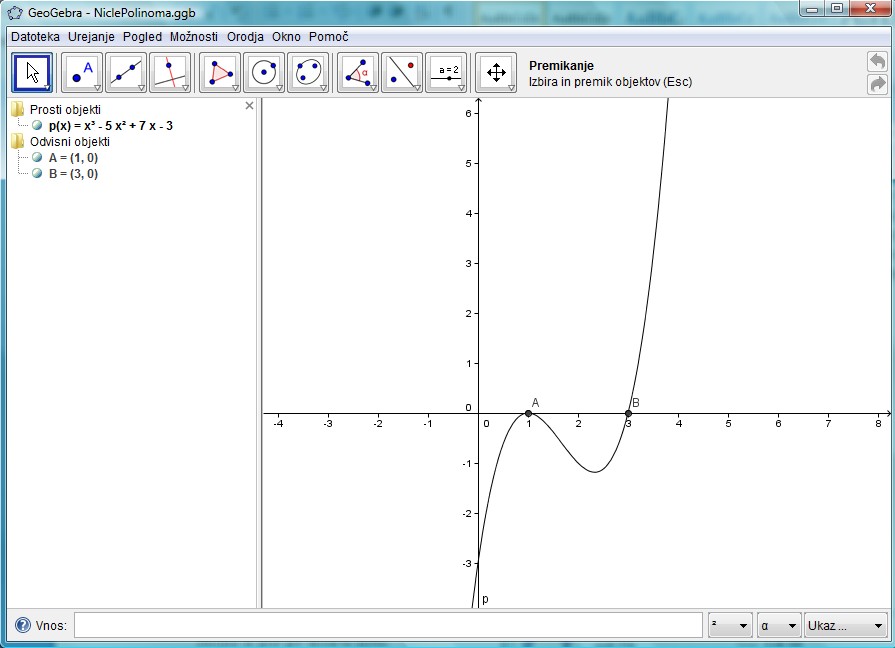
• Če na kratko povzamemo o dobljenih ničlah, je prva ničla 1, katera je dvojna ničla. To pomeni, da se graf samo dotakne abscisne osi oziroma prve ničle. Druga ničla je 3, katera je enojna in graf gre skozi to ničlo.
Potek reševanja s filmom
Ročno reševanje
S pomočjo Hornerjevega algoritma rešimo dani polinom p(x)=x^3-5*x^2+7*x-3, da bomo dobili ničle in sicer tako:

Torej vidimo, da je 1 ničla polinoma p(x). V zadnji vrstici pa smo dobili nov polinom q(x)=x^2-4x+3, ki ga razčlenimo in dobimo q(x)=(x-1)(x-3). Sedaj so naše ničle 1, katera je dvojna ničla in ničla 3, katera je enojna.
Na koncu lahko naredimo tudi preizkus tako, da prvo ničlo vstavimo v prvotni polinom in če dobimo, da je enako 0, je ničla pravilna. Tako preverimo tudi za ostalo ničlo.
Povezava