• S pomočjo programa Geogebra narišemo dani krivulji. Za prvo krivuljo napišemo ukaz y=sqrt(x), kar pomeni sqrt koren. Ukaz za drugo funkcijo pa je y=x^3.

• Sedaj ročno izračunamo integracijski meji:

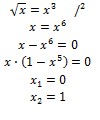
Dobili smo, da sta integracijski meji oziroma, kjer se krivulji sekata 0 in 1.

• Sedaj uporabimo program Maple, kjer bomo izračunali prostornino vrtenine, ter površino vrtenine. Za izračun prostornine vrtenine bomo uporabili formulo:

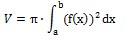
V programu najprej izračunamo prostornino vrtenine krivulje(prve), ki smo jo označili z V1 in nato še prostornino druge krivulje, ki smo jo označili z V2.

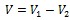
Sedaj prostornino medsebojno odštejemo. Razlika prostornin nam da prostornino lika, omejenega z obema krivuljama.

Za izračun površine vrtenine pa uporabimo formulo:

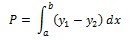
Za y1 sem označila prvo dano krivuljo, za y2 pa drugo dano krivuljo.

Za prostornino vrtenine prve krivulje smo dobili, da je enaka π/2. Prostornina druge krivulje pa je enaka π/4. Prostornina lika je enaka π/4.

Za površino vrtenine pa dobimo, da je enaka 5/12.

• Na začetku si lahko narišemo slikco, da si bomo lažje predstavljali.

• Najprej izračunamo integracijski meji

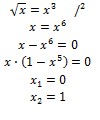
Dobili smo, da sta integracijski meji oziroma, kjer se krivulji sekata 0 in 1.

• Izračunamo prostornino vrtenine ene krivulje, ter nato prostornino vrtenine druge krivulje. Formula:

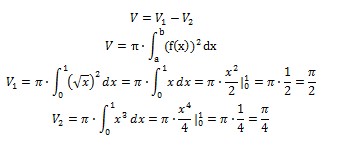
Prostornino medsebojno odštejemo. Razlika prostornin nam da prostornino lika, omejenega z obema krivuljama.

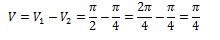
Dobili smo, da je prostornina vrtenine enaka π/4, ki jo oklepata y=√x in y=x^3.

• Izračunamo še površino vrtenine.

Formula:

Dobili smo, da je površina vrtenine enaka 5/12.

Povezava do krivulj: Krivulji.ggb

Povezava do prostornine in površine vrtenine: ProstorninaPovrsinaVrtenine.mw