Graphmatica za Microsoftova okna je računalniški program, namenjen skoraj izključno risanju množic točk v evklidski ravnini IR^2.
Program dobimo na strani: //www8.pair.com/ksoft/
SPLOŠNO O PROGRAMU
Graphmatica za Microsoftova okna je računalniški program, namenjen skoraj izključno risanju množic točk v evklidski ravnini IR^2.
Program dobimo na strani: //www8.pair.com/ksoft/
Značilnosti
• Risanje grafov funkcij, relacij in neenakosti, risanje v polarnih koordinatah ter risanje implicitno in parametrično podanih krivulj; možno je risati tudi rešitve navadnih diferencialnih enačb;
• Na zaslonu je hkrati lahko do 999 grafov;
• Risanje podatkov po točkah in njihovo prileganje krivuljam;
• Številsko reševanje in grafični prikaz dotikalnic (tangent) in integralov;
• Iskanje kritičnih (stacionarnih) točk, rešitev enačb in presečišč kartezičnih funkcij;
• Tiskanje grafov ali njihovo kopiranje v odložišče v obliki .bmp ali .emf v črno-belem ali v barvah.
Tipična zaslonska slika
Program samodejno definira tip grafa na osnovi uporabljenih spremenljivk; prepoznava vrsto enačbe, če je vključena; dinamično spreminja vzorčno lestvico in poskrbi, da je pravilno nameščeno; ponovno izpiše enačbo, če jo preoblikujemo; shrani posebne možnosti, ko nalagamo vsebovan seznam enačb.
Zelo enostavno uporabljamo tipke oziroma ukaze. V orodni vrstici najdemo vse funkcije.
Enačba mora vsebovati:
• Natanko eno odvisno spremenljivko
• Natanko en operator za enačbo ali neenačbo(=,<,<=,>,>=),
• Izraz na obeh straneh
Poljubno lahko dodajamo posebne proste spremenljivke(a,b,c), konstante, različne funkcije(trigonometrične, eksponentne,…) in tudi komentar.
Pri vnosu enačb moramo biti pozorni, da na primer, ko vnesemo cos x, ga ločimo s presledkom, oklepajem ali aritmetičnim operatorjem (razen za edini posebni primer xy). Če bi vnesili cosx, se nam prikaže pojavno okno z izpisom napake.
Primer:
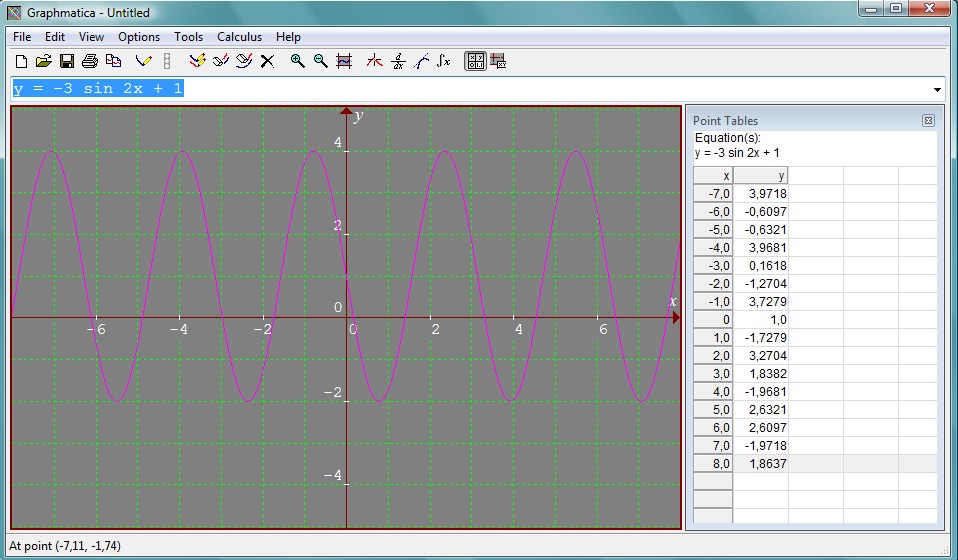
Na desni strani se nam izpišejo koordinate našega grafa. Spodaj je napisano, da je naš graf narisan z roza barvo.
Primeri
• Narišimo graf funkcije podano z enačbo y = sin x. Program nam zelo natančno nariše graf. Spodaj v programu je napisano, da je naš graf narisan z roza barvo.

Na desni strani v programu so napisane koordinate grafa.
• V en koordinartni sistem lahko narišemo tudi več grafov, vendar se bodo obarvali vsak z drugo barvo. V isti koordinatni sistem, kjer imamo narisan prejšnji graf, narišemo še graf y = cos x, y = x^3. Vidimo, da se graf y = cos x obarva v belo barvo, y = x^3 pa v rdečo barvo.
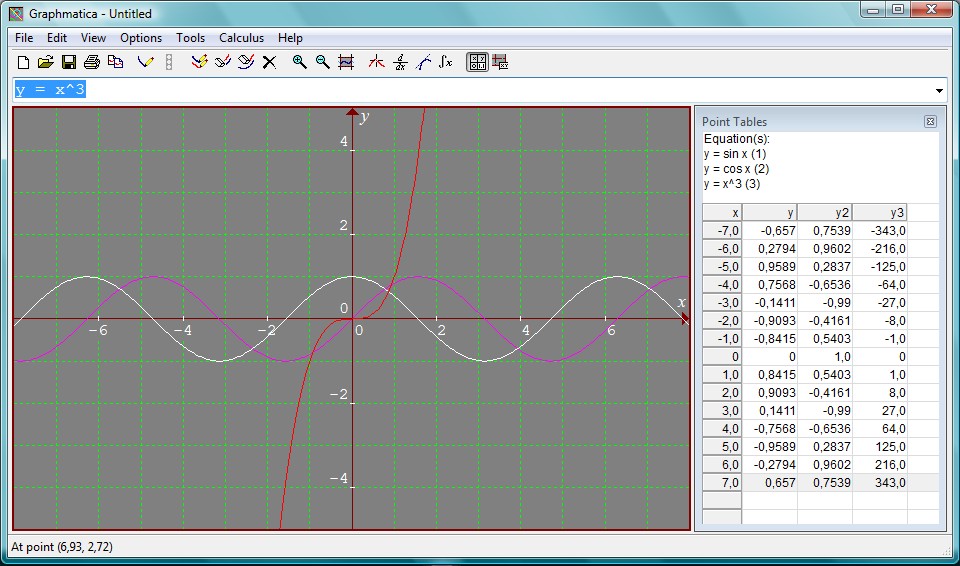
Na desni strani v programu se izpišejo vse tri vnesene enačbe. Pod njimi pa so napisane koordinate, na katerih se posamezni graf nahaja. Koordinata x je za vse tri grafe enaka, koordinata y pa se spreminja za vsak graf. Kot smo grafe narisali po vrsti, tako so tudi označene koordinate y, y2 in y3.
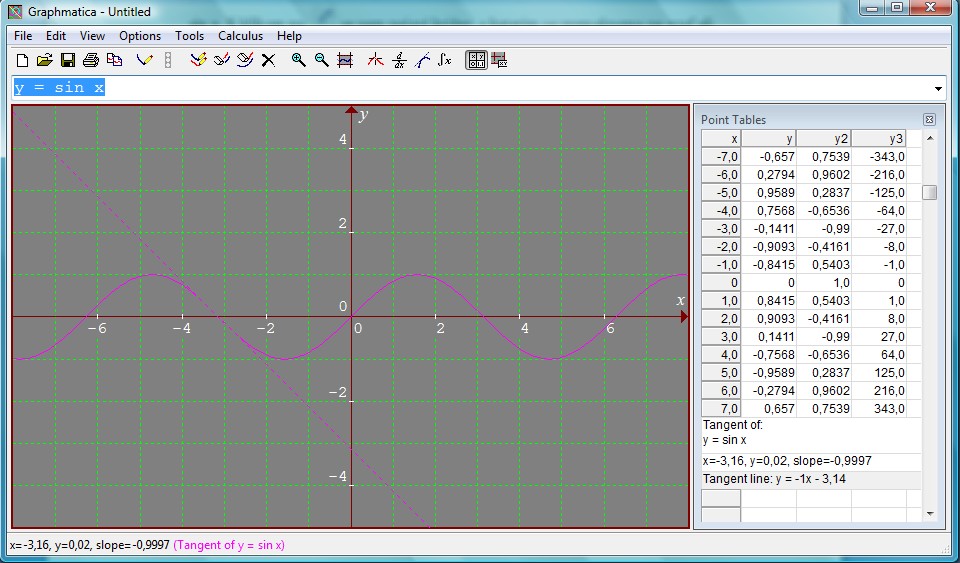
• V programu lahko določimo tudi tangento na graf ali krivuljo. Za primer vzemimo y = sin x. S klikom na
se nam pojavi križec, s katerim se premaknemo na graf ali krivuljo ter kliknemo nanj oziroma nanjo. Spodaj v programu, kjer se zapisujejo naše enačbe, opazimo, da je dodana enačba naše tangente na krivuljo ali graf. Tudi tukaj se nam na desni strani izpišejo koordinate našega grafa.
• V istemu koordinatnemu sistemu lahko določimo integral s klikom na tipko
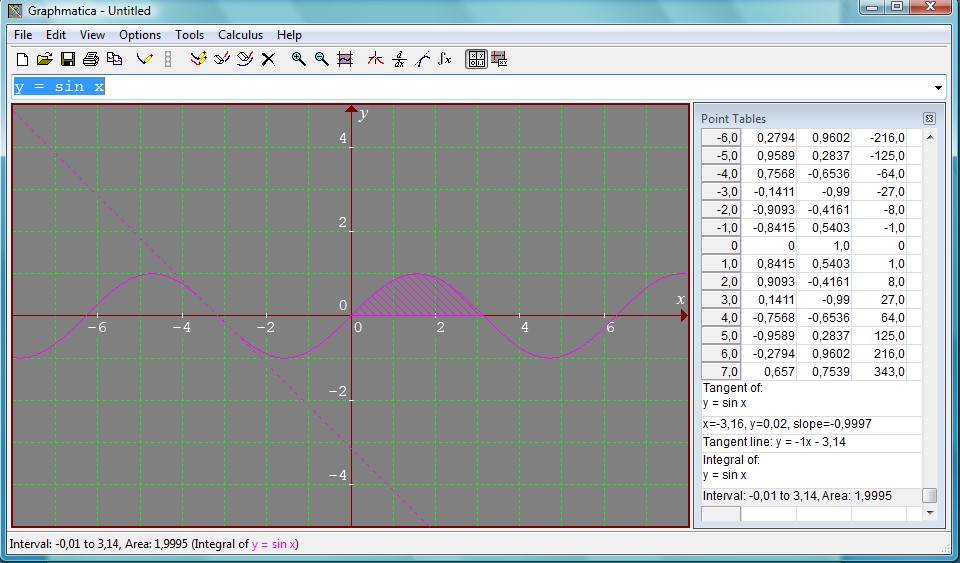
Nato označimo področje integriranja, katero se nam na grafu obarva.
• Ponovno v istemu koordinatnemu sistemu določimo še odvod. To naredimo tako, da kliknemo na gumb
se z miško premaknemo na graf, ter kliknemo najn. Nariše se nam odvod naše enačbe. Če kliknemo na ta graf, se nam bo v oknu za vnašanje enačb izpisalo: y=cos x ' deriv. of y = sin x. Najprej nam napiše odvod enačbe in nato še enačbo katero smo odvajali.
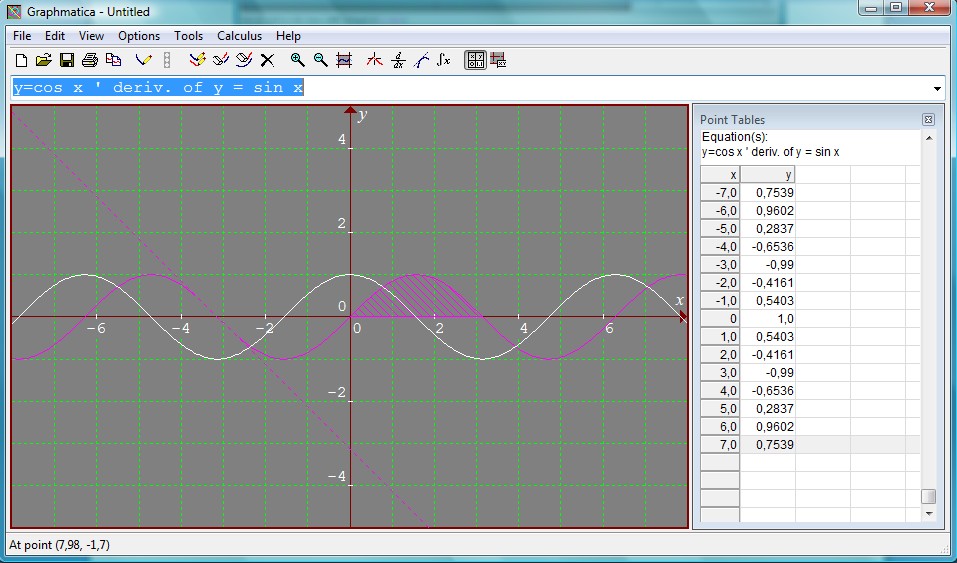
Primerjava z znanimi orodji:
Prednosti:
• Ko smo vnesili enačbo in kliknili Enter se nam je graf dane enačbe takoj narisal, ter na desni strani v programu dobimo napisane koordinate grafa. Na primer pri orodju Geogebra ne dobimo koordinat narisanega grafa.
• Po že narisanemu grafu, želimo dobiti integral. To naredimo tako, da kliknemo samo na gumb za integral in označimo območje integriranja. V Primerjavi z orodjem Maple, gre v Graphmatici mogoče malo bolj hitreje, saj v Malple-u moramo dobiti ukaz s klikanjem ali pa ga kar napišemo.
• V glavnemu oknu orodja lahko zadnji graf pobrišemo z gumbom križec. V programu Geogebra pa je malo več korakov. Pri kateri pobrišemo tako, da kliknemo z desnim klikom miške na graf, ali pa na levi strani okna, ter izberemo Briši. Obstaja pa še ena krajša možnost, kjer kliknemo samo gumb za nazaj.
• Odvod enačbe dobimo, samo s klikom na gumb za odvajanje, ter kliknemo na že narisan graf, katerega želimo odvajati. V primerjavi s programom Maple, moramo napisati funkcijo ali pa jo dobimo s klikanjem.
• Orodje ima mrežast koordinatni sistem, tako, da če imamo narisana dva grafa katera se sekata, lahko že približno vemo kje se sekata. V programu Geogebra nimamo že vnešenega mrežastega koordinatnega sistema tako, da si ga moramo sami nastaviti.
Slabosti:
• Obstaja samo en 'list' kjer lahko vnašamo enačbe. Če bi želeli na drugi nov 'list' vnesiti drugo enačbo, da bo bila na svojemu listu, bi morali prejšnjo shraniti, če jo seveda želimo in nato klikniti nov 'list'. Pri programu Maple, pa imamo lahko več listov.
• Ukaz kot je na primer za koren(sqrt), ga moramo sami vpisati. V programu Maple pa imamo dve izbiri ali s klikanjem ali ga napišemo.
• Ko vnašamo v ukazno okno ukaz na primer sin x, nam orodje pri izpisu nič ne pomaga. V programu Geogebra, ko vnesemo prve črke ukaza nam program pomaga tako, da se prikažejo možne variante na izbiro.
Mnenje o zmožnostih in uporabnosti v povezavi s študijem matematike:
• Orodje nima tako veliko zmožnosti. Pri matematiki bi velikokrat lahko prišel prav pri risanju grafov, saj na desni strani okna izpiše tudi koordinate narisanega grafa in tako, ga na primer bolj natančno narišemo v zvezek.
• Z njim lahko rišemo tudi znane krivulje, za katere si ne predstavljamo kako izgledajo.
• Uporaben je pri računanju odvodov, saj, ko smo kliknili gumb za odvajanje, nam takoj nariše graf, ter, če kliknemo na odvajan graf nam izpiše odvod tega grafa in prvotni graf od katerega se je odvajalo.
• Lahko integriramo, tako, da kliknemo gumb za integriranje, potem, ko imamo že narisan graf.
Povezave