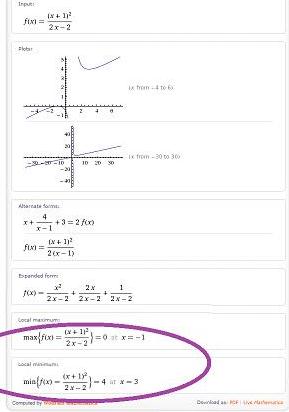
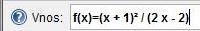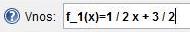Dana je funkcija

• Izračunaj lokalna ekstrema funkcije f.
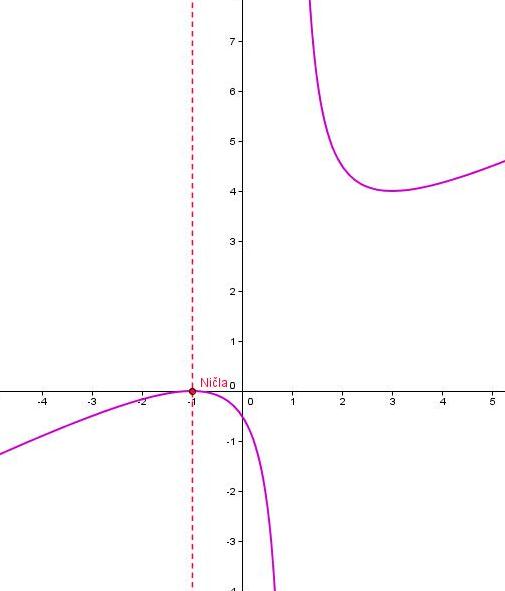
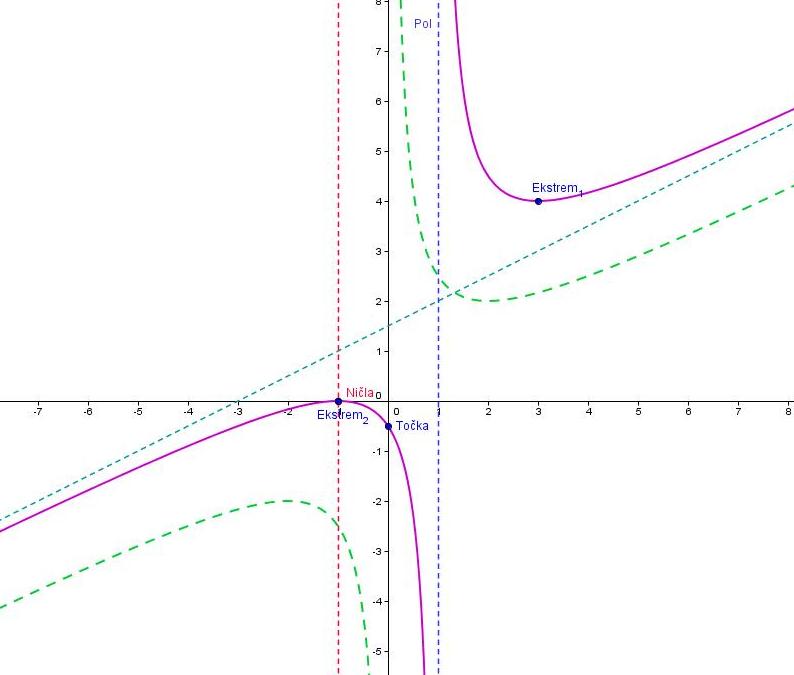
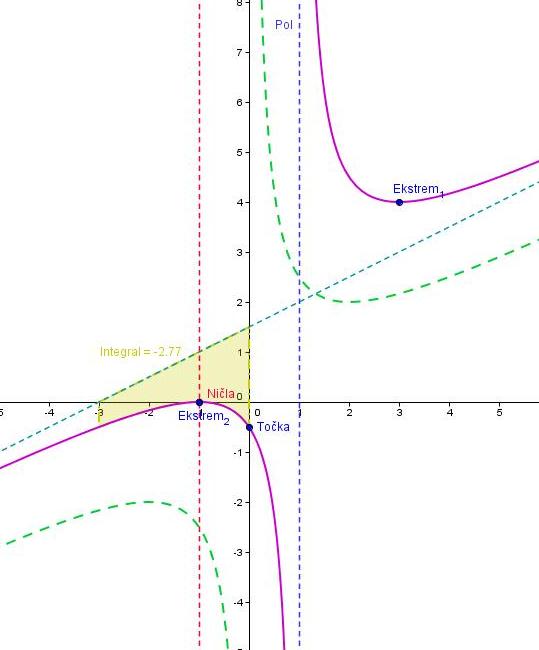
• Izračunajte ničle, pole in simptote ter narišite graf funkcije f.
• Dokažite da je funkcija g(x)=f(x+1)-2 liha.

Matematično ozadje

Pri tej nalogi si bomo pomagali z orodjem Geogebra in WolframAlpha. Z Wolframalpha izračunamo ekstreme, ki jih drugače ročno pridobimo z odvajanjem. Tu si prihranimo veliko dela in časa ter izognemo se površnosti. Narisali in določili bomo pole, poševno asimptoto in dokazali lihost funkcije . Pravilo za lihost se glasi:

.

Abcisi ekstremov:

Ekstrema:

V orodno vrstico vpišemo želeno funkcijo:

Vnos

Rešitev:

Rešitev

NIČLA:

(ničla je soda)

POL:

(navpična asimptota)

POŠEVNA ASIMPTOTA:

Računanje poševne asimptote

Računanje z WolframAlpho

PRESEČIŠČE Z Y OSJO:

LIHOST:

Funkcija g(x) je LIHA!

1.Sprva v vnosno vrstico vpišemo našo funkcijo:

ki sem jo obarvala vijolično.

2.Z ročnim računanjem smo zračunali ničlo, ki smo jo vpisali v GeoGebro (x=-1). Nariše se nam premica. Če želimo dobiti točko moramo zopet uporabiti ukaz za Presečišče dveh objektov (označimo našo premico in funkcijo ). Dobili smo točko, ki sem jo poimenovala Ničla.

Trenutno naša naloga zgleda takole:

3. Narišemo še pol in poševno asimptoto. Oboje vpišemo v vnosno vrstico.

4.Vpišemo točko T(0,-1/2) 5.Vpišemo še ekstrema. Ekstrem1=(3,4) in Ekstrem2=(-1,0) 6.Narišemo še funkcijo , ki sem jo pobarvala v zeleno. Naša dokončana naloga zgleda takole:

7. Če bi si želeli nalogo malo popestriti, bi si lahko izbarali kakšen lik, ki ga oklepajo naše funkcije in premice ter izračunali njegovo ploščino z ukazom Integral[funkcija1,funkcija2,spodnja meja,zgornja meja] V mojem primeru Integral[f(x),f1(x),-3,0]