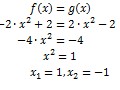• Z ukazom quad(f,a,b) numerično izračunamo določeni integral funkcije f na intervalu [a,b].

• Paziti moramo, da damo funkcijo v enojne navednice, ter ko podamo na primer funkcijo x.^2, je nujno potrebno napisati ločilo pika, kot je prikazano na temu primeru.

Izračun ploščine lika, ki ga omejujeta grafa obeh funkcij.

Dani sta kvadratni funkciji f(x)=-2x^2 in g(x)=2x^2-2. Izračunati moramo ploščino lika, ki ga omejujeta grafa obeh funkcij.

• Najprej ročno izračunamo kje se krivulji sekata. Kjer se sekata imamo ničli.

• To izračunamo tako, da enačbi izenačimo:

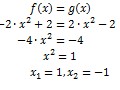
V našemu primeru se krivulji sekata v točkah -1 in 1.

• Nato za izračun ploščine lika, ki ga omejujeta grafa obeh funkcij moramo prvo kvadratno funkcijo f(x)=-2x^2 odšteti od druge kvadratne funkcije g(x)=2x^2-2, ter dobimo h(x)=-4x^2+4 v mejah od -1 do 1. Meji predstavljata ničli.

• Sedaj za izračun ploščine lika uporabimo ukaz quad, ter napišemo: ploscina=2*(quad('-4*x.^2+4',-1,1)) Pri temu smo ukaz poimenovali ploscina.

Ta ukaz nam izračuna integral funkcije h(x)=-4x^2+4 v mejah od -1 do 1. Integral smo pomnožili z 2, ker imamo dve polovici, kateri loči x os, ter dobimo ploščino lika, ki ga omejujeta grafa obeh funkcij. Končni rezultat ploščine lika je 10.6667.

>> ploscina=2*(quad('-4*x.^2+4',-1,1))

ploscina =

10.6667