V danem naravnem številu je zadnja neničelna števka najbolj desna neničelna števka v desetiškem zapisu števila. Na primer, zadnja neničelna števka števila 123 je 3, pri številu 45600 je to 6, pri številu 100 pa 1.
Napiši funkcijo, ki za vsako števko od 1 do 9 ugotovi, kolikokrat se pojavi kot zadnja neničelna števka v zaporedju M,M + 1,M + 2, . . . ,N − 2,N − 1,N. Funkcija naj zapiše rezultat v tabelo tipa int[9]. Na primer, če je M = 118 in N = 122, pomeni, da obravnavamo zaporedje 118, 119, 120, 121, 122. Zadnje neničelne števke so 8, 9, 2, 1 in 2. Torej mora tabela vsebovati elemente 1, 2, 0, 0, 0, 0, 0, 1, 1, ker enica, osmica in devetka nastopajo kot zadnja neničelna števka enkrat, dvojka pa dvakrat.
Pozor: Razlika med številoma N in M je lahko tako velika, da je bolje, če ne obravnavamo vsakega števila med M in N posebej, ker bi podprogram predolgo tekel. Tvoja podprogram naj bo učinkovit!

OPIS PROBLEMA

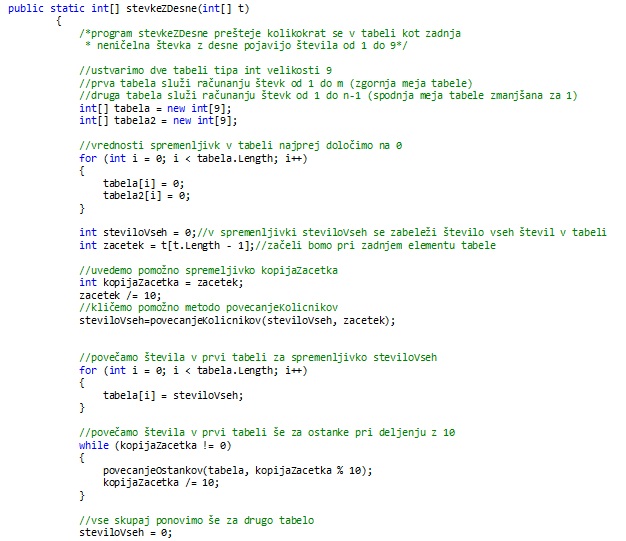
Podano je zaporedje števil. Prešteti je potrebno vse zadnje neničelne števke v zaporedju. Na koncu vrnemo tablo števil velikosti 9. V tabeli mora biti število ponovitev števil od 1 do 9 kot zadnje neničelne števke.

IDEJA REŠITVE

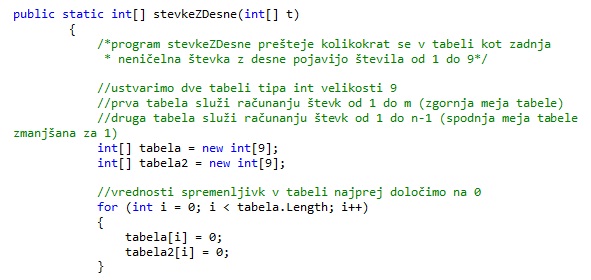
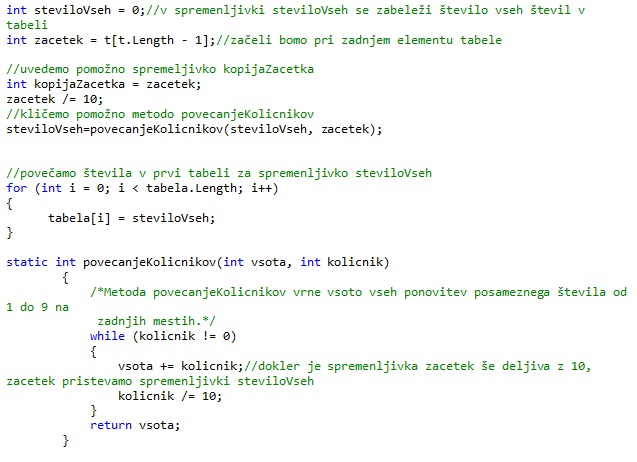
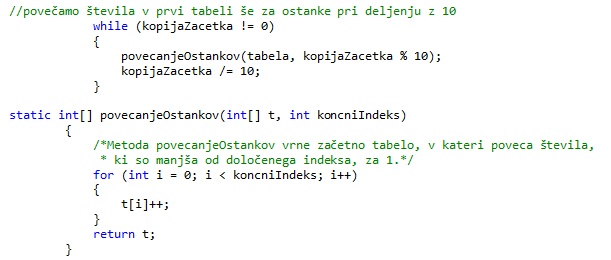
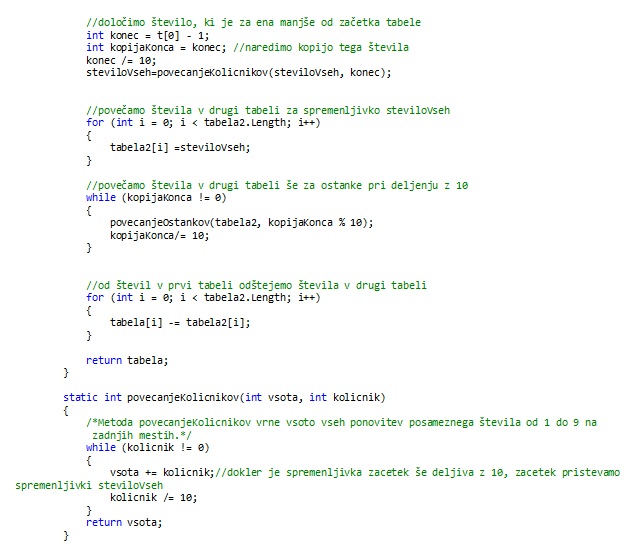
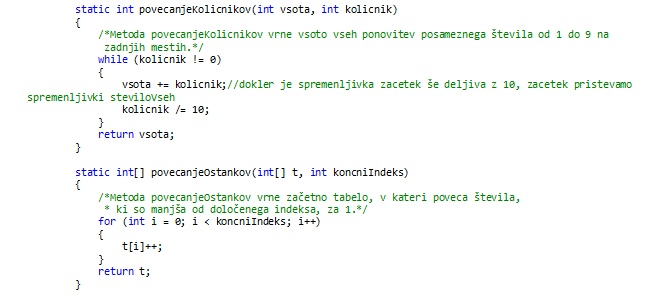
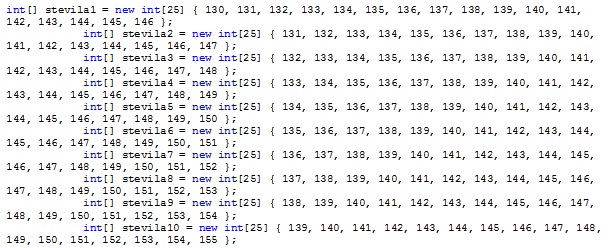
Najprej ustvarimo dve tabeli velikosti 9, v katerih se bo beležilo število ponovitev. V prvi tabeli bomo dobili število ponovitev števil od 1 do 9 na zadnjih mestih, za števila od 1 do m. Pri čemer m predstavlja zgornjo mejo intervala. V drugi tabeli pa bomo dobili število ponovitev števil od 1 do 9 na zadnjih mestih, za števila od 1 do n-1. Pri čemer je n-1 število, ki je predhodnik števila, ki predstavlja spodnjo mejo intervala. Najprej bomo ustreznokrat povečali števila pri deljenju z 10 (tolikokrat se zaporedje od 1 do 9 ponovi). Nato bomo poskrbeli še za ostanke pri deljenju z 10. Pri ostankih bomo ustreznokrat povečali števila v prvi oziroma drugi tabeli do indeksa, ki ga predstavlja ostanek pri deljenju z 10.

Program stevkeZDesne bo kot vhodni podatek prejel tabelo zaporedja celih števil. Najprej ustvarimo dve celoštevilski tabeli velikosti 9 in nastavimo vse vrednosti tabel na 0.

Nato ustvarimo dve celoštevilsko spremenljivki. Prva celoštevilska spremenljivka je steviloVseh, v kateri bomo korakoma shranjevali število ponovitev posamezne števke. Druga celoštevilska spremenljivka pa je zacetek, kateri nastavimo zacetno vrednost na zgornjo mejo intervala. Poleg teh dveh spremenljivk ustvarimo še pomožno spremenljivko kopijaZaceteka, katera nam služi za pomnenje vrednosti v spremenljivki zacetek.
Nato pokličemo pomožno metodo povecanjeKolicnikov, ki kot vhodni argument sprejme dve celi števili. Ti dve števili sta steviloVseh in zacetek. Znotraj metode s pomočjo while zanke poskrbimo, da se steviloVseh ustreznokrat poveča. To pa poteka tako, da na vsakem koraku spremenljivko zacetek delimo z 10. Količnik pri deljenju z 10 pa predstavlja število ponovitev posamezne števke, zato ga prištejemo k spremenljivki steviloVseh. While zanka se zaključi, ko je spremenljivka zacetek enaka 0. Metoda kot rezultat vrne ustreznokrat povečano spremenljivko steviloVseh.
S for zanko se nato sprehodimo skozi prvo tabelo ter hkrati vse elemente tabele povečujemo za spremenljivko steviloVseh.

Ostanejo nam le še ostanki. Ponovno uporabimo while zanko znotraj katere kličemo pomožno metodo povecanjeOstankov. Pomožna metoda, kot vhodni podatek sprejme prvo tabelo in celo število, katerega predstavlja ostanek pri deljenju spremenljivke kopijaZacetka z 10. Ta pomožna metoda poveča števila v vhodni tabeli, ki ležijo na indeksih manjših od ostanka. Metoda na koncu vrne vhodno tabelo, v kateri so števila na ustreznih indeksih povečana. While zanka se ponavlja dokler je ostanek različen od 0.

Vse to kar smo do sedaj opisali naredimo tudi za drugo tabelo. Razlika je le pri zgornji meji. Za drugo tabelo shranimo zgornjo mejo v celoštevilsko spremenljivko konec. Kot zgornjo mejo pa vzamemo predhodnika števila n (n je prvi element tabele, torej element na indeksu 0).

Ko vse skupaj ponovimo še za drugo tabelo, še vrednosti, ki smo jih dobili v drugi tabeli, odštejemo od vrednosti, ki smo jih dobili v prvi tabeli. Pri tem si pomagamo s for zanko, s katero se sprehodimo skozi obe tabeli. Sočasno vrednosti na enakih indeksih med seboj odštevamo. Od vrednosti na indeksu i v prvi tabeli odštejemo vrednost na indeksu i v drugi tabeli.

Metoda vrne prvo tabelo, v kateri je shranjeno število ponovitev posamezne števke na zadnjih mestih na intervalu od n (element v tabeli na indeksu 0) do m (element v tabeli na indeksu t.Length -1).

Za testne primere sem si izbrala različne tabele števil. Poudarek pri različnosti je bil v tem, da se je prvo število v tabeli vedno končalo z drugim številom. Tako sem sestavila 10 testnih primerov.