- Boruvka prvič leta 1926 objavi algoritem kot metodo za učinkovito konstruiranje električnega omrežja na Moravskem;
- kasneje so ga odkrivali tudi mnogi drugi (Choquet, Florek, Lukasiewicz, Perkal, Steinhaus, Zubrzycki, Sollin).
Boruvka je bil češki matematik, danes najbolj znan za svoje delo v teoriji grafov.

Otakar Boruvka (1899-1995)
Minimalno vpeto drevo v grafu - Boruvkov algoritem
ZGODOVINA
MINIMALNO VPETO DREVO
KAJ JE DREVO?
- Je povezan graf, brez ciklov (Pojem_graf);
- če ima drevo n vozlišč, ima n-1 povezav;
- če v drevesu odstranimo katerokoli povezavo ni več povezan graf.
KAJ JE VPETO DREVO?
- Vpeto drevo je podgraf grafa, ki vsebuje vsa vozlišča originalnega grafa;
- je povezan in brez ciklov;
- graf ima lahko več vpetih dreves.
KAJ JE MINIMALNO VPETO DREVO?
- Predpostavimo da imamo dan neusmerjen utežen graf;
- Minimalno vpeto drevo je podgraf grafa, ki vsebuje vsa vozlišča (brez ciklov). Veljati mora, da je njegova skupna teža povezav (vsota uteži povezav) minimalna. Minimalno vpeto drevo je torej tisto vpeto drevo, ki ima težo(vsota vrednosti vseh povezav drevesa) manjšo ali enako teži drugih vpetih dreves v grafu.
KOLIKO MINIMALNO VPETIH DREVES JE LAHKO V DANEM GRAFU?
Različni postopki iskanja minimalno vpetega drevesa lahko v splošnem vrnejo različna minimalno vpeta drevesa. V primeru, da obstajajo v grafu povezave z enakimi utežmi, je možnih več minimalno vpetih dreves. Če so vse uteži različne, obstaja natanko eno vpeto minimalno drevo.
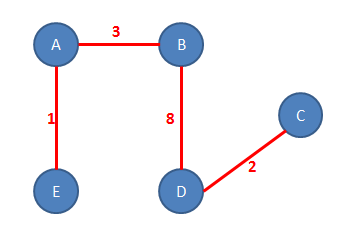
PRIMER MINIMALNO VPETEGA DREVESA
|
Za iskanje minimalno vpetih dreves, poznamo več algoritmov: Primov algoritem Primov_algoritem, Kruskalov algoritem Kruskalov_algoritem,Chazellov algoritem Chazellov algoritem, tukaj pa bomo spoznali Boruvkov algoritem.
BORUVKOV ALGORITEM
BORUVKOV ALGORITEM je algoritem za iskanje minimalno vpetega drevesa v neusmerjenem uteženem grafu Utežen_graf.
PROBLEM
Imamo dan neusmerjen graf z uteženimi povezavami (uteži so pozitivna realna števila). Cilj je poiskati vpeto drevo znotraj tega grafa, kjer bo vsota uteži posameznih povezav v drevesu minimalna (uporabimo lahko samo povezave, ki so v originalnem grafu, povezav ne dodajamo).
POSTOPEK
Vsako vozlišče vzame najcenejšo sosednjo povezavo. Z najcenejšo povezavo med seboj povežemo sosednja vozlišča. Med seboj tako dobimo povezana vozlišča (nekatera ali vsa). Če po prvem koraku še ne dobimo drevesa, vpetega nad vsemi vozlišči, postopek ponovimo tako, da poiščemo skupine povezanih vozlišč (poddrevesa) in ponovimo postopek, vsako poddrevo vzame najcenejšo povezavo do sosednjega poddrevesa. Nadaljujemo toliko časa, dokler ne nastane drevo, vpeto nad vsemi vozlišči grafa.
Da boš bolje razumel/a postopek algoritma si poglej primere na naslednjih prosojnicah, ki sledijo (Primeri).
UPORABA
Električno omrežje
Želimo izračunati koliko bi nas najmanj stali stroški postavitve električnega omrežja med določenimi kraji, ki so bili dosedaj brez električne energije. Vsak kraj mora biti povezan z drugim krajem z električnim kablom, kable polagamo tako, da so stroški najmanjši.
Klepetulje
Katja ima n prijateljic. Vse rade klepetajo po telefonu. Vsako novo novico morajo izvedeti vse. Stroški telefona so zelo visoki, zato so nekaj časa spremljale stroške povprečnega pogovora. Ugotoviti moramo, kako naj se kličejo, da bodo za razširitev ene novice porabile čim manj denarja.
In še in še
Algoritem je zelo uporaben, saj ga lahko uporabimo pri reševanju problemov iz vsakdanjega življenja. Poznati moramo le točke (kraji, trgovine...) ter povezave med njimi, ki so utežene s cenami ali časom.
PRIMERI

PRIMER 1
Poiskati moramo minimalno vpeto drevo danega grafa na 7 točkah.
Dan je graf:
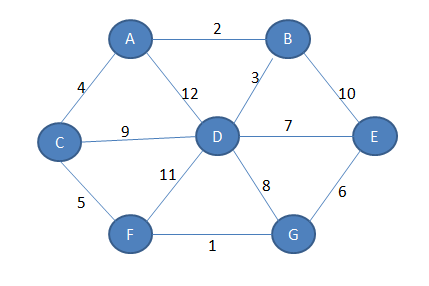
Iz vsake točke poiščemo najcenejšo povezavo
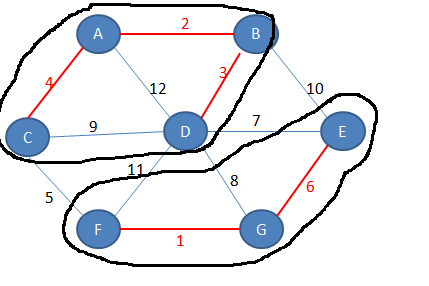
Dobimo dve poddrevesi: ABCD in EFG. Sedaj poiščemo najcenejšo povezavo iz prvega poddrevesa. Možne so povezave CF, DF, DG, DE in BE. Najcenejša je povezava med C in F. Iz drugega poddrevesa so v prvo poddrevo možne iste povezave. Povežemo torej C in F.
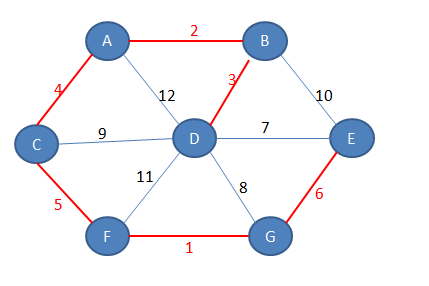
Dobimo minimalno vpeto drevo. Povezali smo vsa vozlišča, tako da smo pri tem minimizirali teže povezav.
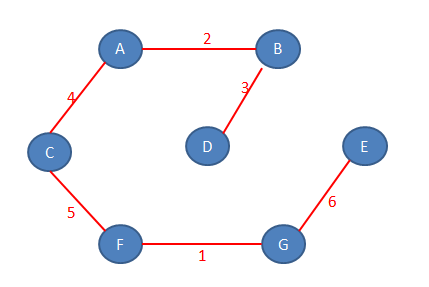
Končna slika minimalno vpetega drevesa. Skupna minimalna teža povezav je 21.
PRIMER 2
V kampu Adria v Ankaranu so se odločili postaviti mobilne hišice, kjer bodo lahko počitnikovali njihovi gostje. Zanima jih koliko bi najmanj znašali stroški postavitve električnega omrežja med 14 hišicami, ki trenutno še nimajo elektrike.
Rešitev problema je predstavljena v spodnjem filmčku:
PRIMER 3
Podana je spodnja matrika. Poiščimo minimalno vpeto drevo.
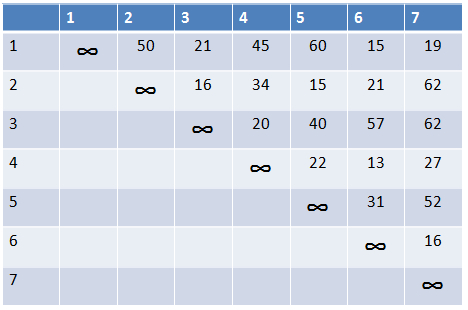
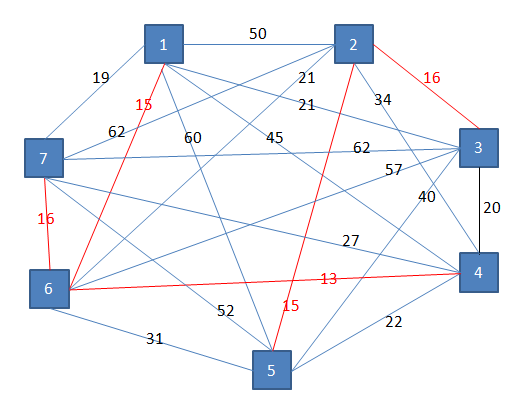
Na osnovi matrike narišemo graf.
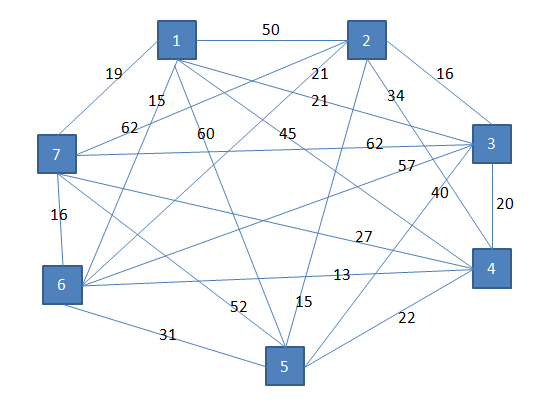
PRIMER3 - nadaljevanje
Rešimo problem. Iz vsake točke poiščemo najcenejšo povezavo. Najcenejše povezave so:
- iz točke 1 v točko 6: cena 15
- iz točke 2 v točko 5: cena 15
- iz točke 3 v točko 2: cena 16
- iz točke 4 v točko 6: cena 13
- iz točke 5 v točko 2: cena 15
- iz točke 6 v točko 4: cena 13
- iz točke 7 v točko 6: cena 16
Dobimo dve poddrevesi: 1467 in 235.
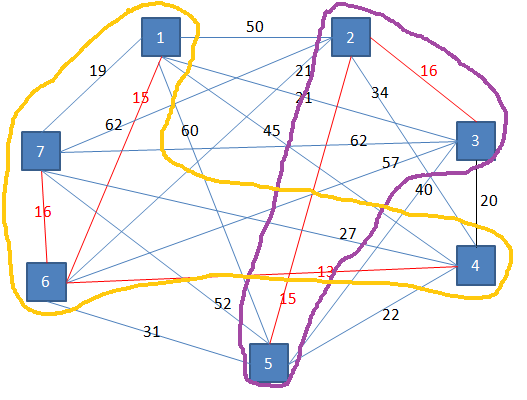
Poiščemo najcenejšo povezavo iz prvega poddrevesa. Možne povezave so: 12, 13, 15, 42, 43, 45, 62, 63, 65, 72, 73 in 75. Najcenejša povezava je med 4 in 3 s ceno 20. Iz drugega poddrevesa so v prvo poddrevo možne iste povezave. Povežemo torej 4 in 3.
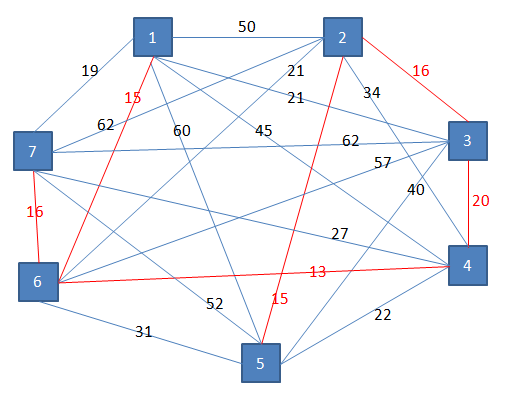
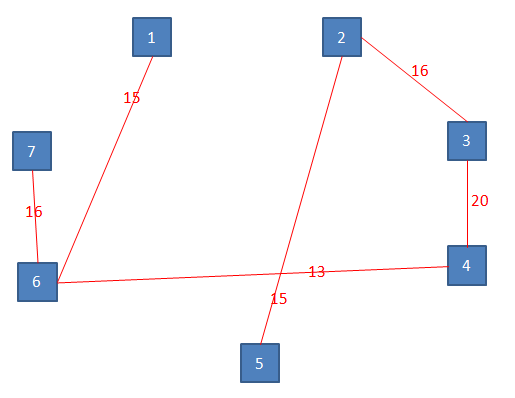
Dobimo minimalno vpeto drevo. Skupna minimalna teža povezav je 95.
PRIMERJAVA ALGORITMOV PRIMOV/KRUSKALOV/BORUVKOV
Vse tri algoritme uporabljamo za iskanje minimalno vpetega drevesa v danem grafu.
Primov algoritem: že zgrajenemu drevesu dodajamo najbolj optimalno razpoložljivo povezavo, dokler niso vsa vozlišča povezana v drevesu.
Kruskalov algoritem: vedno izbiramo najbolj optimalno povezavo med obstoječimi vozlišči, dokler ni zgrajeno drevo. Pazimo na cikle.
Boruvkov algoritem: deluje tako, da vsako vozlišče pograbi najcenejšo povezavo. Če po prvem koraku še ne dobimo drevesa, se postopek ponovi na skupinah vozlišč.
Vsi trije algoritmi so »požrešni« algoritmi, kar pomeni, da zmeraj, na vsakem koraku, izberemo najboljše tisti hip.
Primov algoritem je vedno časovne zahtevnosti O(n2). Kruskalov algoritem je časovne zahtevnosti za graf, ki je blizu polnemu, O(n2 * log(n)), za graf, v katerem število povezav ni mnogo večje kot število vozlišč je časovna zahtevnost O(n*log(n)).
KVIZ
VPRAŠANJE 1
Pravilno
Bravo! Odgovoril/a si pravilno. NaprejNapačno
Odgovor ni pravilen. Poskusi ponovno Ponovno
Namig: Odgovor najdeš na naslednji prosojnici.
VPRAŠANJE 2
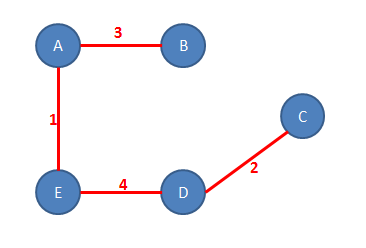
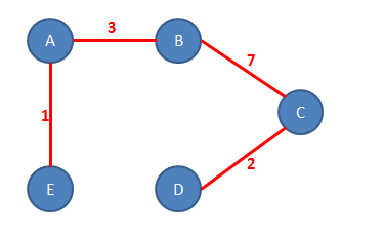
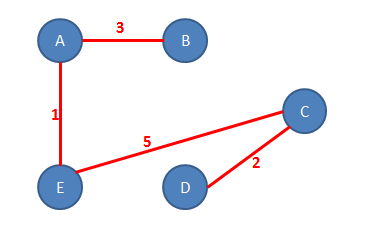
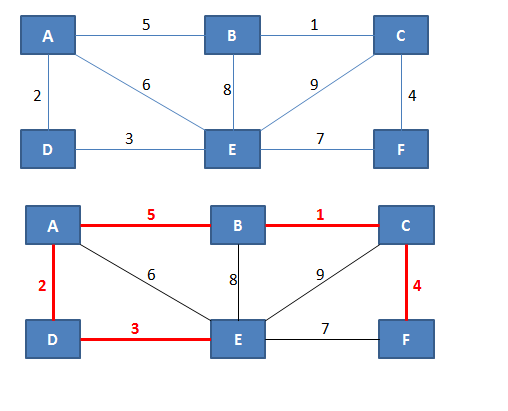
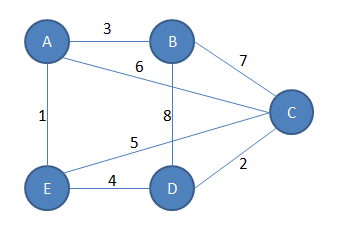
2. Katera od spodnjih slik predstavlja minimalno vpeto drevo za dani graf?
|
Pravilno
Bravo! Odgovoril/a si pravilno. NaprejNapačno
Odgovor ni pravilen. Poskusi ponovno. Ponovno
Namig: Skupna vsota uteži na posameznih povezavah mora biti minimalna.
VPRAŠANJE 3
Pravilno
Bravo! Odgovoril/a si pravilno. Zaključi kvizNapačno
Odgovor ni pravilen. Poskusi ponovno. Ponovno
Namig: Odgovor najdeš na naslednji prosojnici.
LITERATURA IN VIRI
- Prosojnice in zapiski iz predavanj Računalništvo 1
- Podatkovne strukture in algoritmi, Jernej Kozak, Ljubljana 1984
- //penelope.fmf.uni-lj.si/psawiki/images/c/c6/Seminarska-Boruvka.pdf
- //www-history.mcs.st-and.ac.uk/Biographies/Boruvka.html
- //penelope.fmf.uni-lj.si/r2wiki/index.php/Kruskalov_algoritem/Minimalno_vpeto_drevesa
- //sl.wikipedia.org/wiki/Minimalno_vpeto_drevo
- //en.wikipedia.org/wiki/Bor%C5%AFvka%27s_algorithm
- //www.ics.uci.edu/~eppstein/161/960206.html
- //wiki.fmf.uni-lj.si/wiki/Primov_algoritem
- //en.wikipedia.org/wiki/Minimum_spanning_tree
- //www.google.si/url?sa=t&source=web&cd=4&ved=0CCwQFjAD&url=http%3A%2F%2Fciteseerx.ist.psu.edu%2Fviewdoc%2Fdownload%3Fdoi%3D10.1.1.88.8975%26rep%3Drep1%26type%3Dpdf&rct=j&q=Chazellov%20algoritem&ei=mu0ZTtudJcTX8gPduagR&usg=AFQjCNHXZfhIwq7NBkdyH6W817R5NW9wtw&cad=rja