Teorija grafov je veja matematike, ki preučuje lastnosti grafov. Je obširno in splošno uporabno področje matematike, ki se v zadnjih desetletjih naglo razvija.

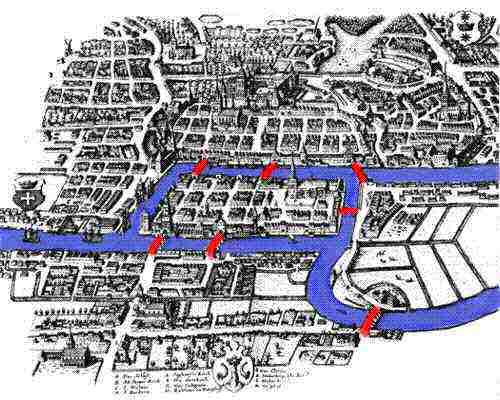
Za začetnika teorije grafov velja švicarski matematik Leonhard Euler, ki je leta 1736 v svoji rešitvi Problema mostov v mestu Königsberg opisal osnovne koncepte teorije grafov, kot so vozlišča, povezave in stopnja vozlišča. Več

Slika 1: Solutio problematis ad geometriam situs pertinentis

Njen razvoj se kaže tudi v tesnem stiku z razvojem elektrotehnike, računalništva in digitalne tehnologije. Njeni izsledki so izredno uporabni tudi v kemiji, biologiji, bioinformatiki, lingvistiki in na veliko družboslovnih področjih, na katerih se srečujemo z analizo omrežij in njihovih lastnosti.

Zakaj razumeti teorijo grafov?

• Skupek koristnih tehnik za reševanje resničnih problemov - predvsem za različne vrste optimizacije.
• Teorija grafov je uporabna za analizo "stvari, ki so povezane z drugimi stvarmi", ki se uporablja skoraj povsod.
• Nekateri težji problemi postanejo lahki, ko so zastopani z uporabo grafa.
• Obstaja veliko nerešnih vprašanj v teoriji grafov: reši eno in postani bogat in slaven. ?

Graf sestavlja neprazna množica elementov, ki jih poimenujemo točke grafa ali vozlišča in seznam (neurejenih) parov teh elementov, ki jih imenujemo povezave grafa. Množico točk grafa označimo z , seznam povezav pa z . Če sta točki grafa , potem za povezavi ali rečemo, da povezujeta točki in .

Uteženi graf ali omrežje je graf, v katerem je vsaki povezavi prirejeno pozitivno število, ki ga imenujemo utež.

Uteženi graf je lahko usmerjen ali neusmerjen, ciklični ali aciklični tako kot neuteženi graf.

Usmerjen graf je tisti graf, ki ima vse povezave usmerjene. Iz ene točke se premaknemo v drugo le v smeri povezave, nazaj pa po isti poti ne gre, razen če je le ta dvosmerna.

Slika 2: Usmerjeni uteženi graf

Vse povezave so označene s številom, ki je realno število in lahko pomeni:

• razdalja med dvema lokacijama (kraji, računalniki v omrežju),
• potreben čas, da se pride iz enega vozlišča v drugo vozlišče (postaje, države v časovnem načrtu)
• stroški povezav (vozovnice, stroški kablov)

Mnogi sistemi v resničnem svetu so lahko opisani s kompleksnimi omrežji. Vozlišča v omrežju predstavljajo posameznike (objekte) in povezave predstavljajo interakcije med posamezniki (objekti). Večina realnih omrežij so utežena omrežja, kjer so količine na povezavah bistvenega pomena za celoten opis teh omrežij.

Kje se omrežja največ uporabljajo?

Prometna omrežja

V svetovnem omrežju letališč je vsaka povezava dana z utež (promet), ki predstavlja število razpoložljivih sedežev na direktnih letalskih povezavah med letališčem i in j.

Omrežja sodelovanj

V primeru omrežja znanstvenega sodelovanja, vozlišča predstavljajo avtorje in utež označuje število dokumentov soavtorjev. Se pravi, koliko imata avtorja skupnih dokumentov, kjer sta oba podpisana.

Socialna omrežja

Spletna socialna omrežja, kot so MySpace in Facebook, imajo milijone registriranih uporabnikov, kjer je vsak uporabnik povezan s številnimi drugimi preko prijateljstva, poklicnih združenj (ki so članice skupnosti) in tako naprej. Posledično, struktura grafa ima na milijone vozlišč (uporabniki ali družbeni akterji) in povezav (družbene vezi). Model uteženega grafa se uporablja za analizo oblikovanja skupnosti znotraj omrežja, ciljno trženje in oglaševanje, modeliranje strukture in dinamike, kot so mnenjska formacija. Uporablja se tudi za anliziranje omrežij z namenom povečati širjenje informacij prek socialnih povezav.

Graf je najbolj univerzalna podatkovna struktura, ki je lahko predstavljena na več načinov.

Pogledali si bomo najpogostejši obliki predstavitve grafa:

• z matriko sosednosti
• seznamom sosednosti

Matrika sosednosti je kvadratna matrika velikosti , kjer je n število vseh vozlišč omrežja ali grafa. Če obstaja povezava med vozliščem in vozliščem , je vrednost njune povezave oz utež (). Če povezava med tema dvema vozliščema ne obstaja, je vrednost enaka 0, lahko se označi tudi s simbolom za neskončnost.

Primer1: Za neusmerjen graf je matrika sosednosti simetrična.

Slika 3: Neusmerjen uteženi graf

Primer2: Usmerjen graf.

Slika 4: Usmerjen uteženi graf

dodajVozlišče()

• če vozlišče ne obstaja v matriki

  • ustvari vozlišče
  • matrika A je za 1 vrstico in 1 stolpec večja
    

dodajPovezavo(, , )

• če eden od dveh vozlišč ne obstaja

  • dodajVozlišče()

• če oba vozlišča ne obstajata

  • dodajVozlišče(), dodajVozlišče()

• če povezava med in ne obstaja

  • 
    

odstraniPovezavo(,, )

• če povezva med in obstaja

  • 
    

spremeniVrednostPovezav(, , )

• če povezva med v_i in v_j obstaja

  • A[i][j] = w_{ij}
    

V seznamu sosednosti se za vsako vozlišče hrani seznam vseh tistih vozlišč, s katerimi je povezan. Vsak element seznama vsebuje informacijo o sosednosti in vrednosti njegove povezave.
Primer1: Usmerjen uteženi graf.

Slika 5: Usmerjen uteženi graf

Primer2: Neusmerjen uteženi graf.

Slika 6: Neusmerjen uteženi graf

Spodaj v filmčku je potek reševanja po korakih.

dodajVozlišče()

• če vozlišče ne obstaja v seznamu

  • ustvari vozlišče
  • trenutno je brez povezave, kazalec kaže na NULL
    

dodajPovezavo(, , )

• če eden od dveh vozlišč ne obstaja

  • dodajVozlišče()

• če oba vozlišča ne obstajata

  • dodajVozlišče(), dodajVozlišče()

• če povezva med in ne obstaja

  • .naslednji() =
  • .naslednji() =
    
  • .nasled() =

odstraniPovezavo(, , )

• če povezva med in obstaja

  • sprehodimo se po zanki, dokler naslednji od enak , s katerim je povezan
    

    • .naslednji() = .naslednji()naslednji()

spremeniVrednostPovezav(, , )

• če povezva med in obstaja

  • sprehodimo se po zanki, dokler naslednji od enak , s katerim je povezan
    

    • spremenimo vrednost

Iz vidika prostorske zahtevnosti:

• Matrika sosednosti

  • ne uporablja kazalce
  • je bolj učinkovita za t.i. goste matrike (matrike z veliko povezav)
  • , vozlišč povezav, ko je graf blizu polnemu grafu ?

• Seznam sosednosti

  • vsebuje le informacije o povezavah, ki se pojavijo v grafu
  • je bolj učinkovita za t.i. redke matrike (matrike z malo povezav)
  • , kjer je pri neusmerjenih grafih vsaka povezava našteta dvakrat

Iz vidika čaovne zahtevnosti:

• Matrika sosednosti

  • zaradi indeksacije je primerna za preverjanje izbranih povezav
  • vrednosti povezav so dosegljive v konstantnem času

• Seznam sosednosti

  • primerna za aplikacije, ki obravnavajo poti v grafu

Teorija grafa
Uteženi graf in algoritmi
Uteženi graf - Wiki
Uteženi graf - seminarska

Jon J. Watkins, Robin J. Wilson: Uvod v teorijo grafov