2-3-4 (imenujemo tudi 2-4) drevo, ki je iskalno drevo ni pa dvojiško. To jeB drevo reda 4. Drevo reda 4 pomeni, da se lahko v vozlišču nahajajo 1, 2 ali 3 podatki in slednja vozlišča imajo 2, 3 ali 4 sinove.

Primer

• 1 element v vozlišču očeta ima dva sinova

  

• 2 elementa v vozlišču očeta imata tri sinove

  

• 3 elementi v vozlišču očeta imajo štiri sinove

  

2-3-4 drevo je iskalno, ki je lahko prazno ali ne prazno

• v vsako vozlišče lahko shranimo do tri vrednosti
• vsako vozlišče ima lahko 2, 3 ali 4 sinove
• vsa vozlišča (listi) 2-3-4 drevesa so na isti globini
• pri 2-3-4 drevesu lahko elemente iščemo, vstavljamo ali brišemo

Elemente v 2-3-4 drevesu iščemo podobno kot v iskalnem dvojiškem drevesu. Iskanje se začne v korenu. Razlika je v tem da v iskalnem dvojiškem drevesu primerjamo samo z enim elementom v vozlišču, pri 2-3-4 drevesu primerjamo z vsemi elementi v danem vozlišču. V primeru da se iskani element ne nahaja v vozlišču, določimo pot po katerem sinu bomo iskanje nadaljevali. Če v 2-3-4 drevesu ni območja s sinom iskanega elementa, potem drevo ne vsebuje iskanega podatka.

Iskanje na primeru

1. V 2-3-4 drevesu poišči element 15

   
   • Elenent 15 začnemo iskati v korenu. V korenu ga ni, pot nadaljujemo v levo poddrevo, ker je 15 manjše od 20. Preverimo naslednje vozlišče, 13 je manjše in 17 večje od 15, pot nadaljujeno v sredinsko vozlišče. Prišli smo do vozlišča z elementom 15, iskanje je zaključeno.

2. V 2-3-4 drevesu poišči element 22

   
   • Element začnemo iskati v korenu. V korenu ga ni, pot nadaljujemo v desno poddrevo, kjer sta elementa 26 in 34 večja od 22. Pot nadaljujemo v levo vozlišče, kjer se nahaja element 23, ki je večje od 22. Tako bi pot nadaljevali v levem vozlišču, vendar je vozlišče prazno. V tem primeru danega elementa ni v 2-3-4 drevesu, iskanje je zaključeno.

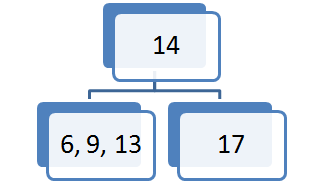
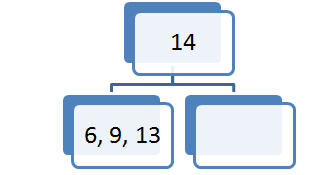
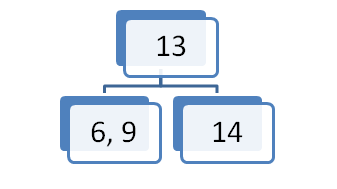
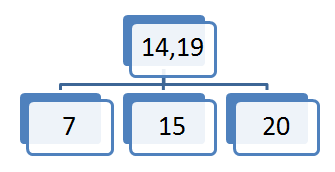
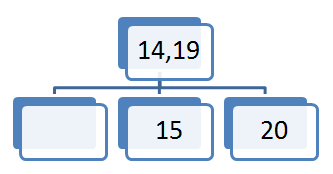
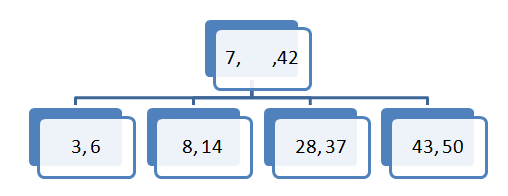
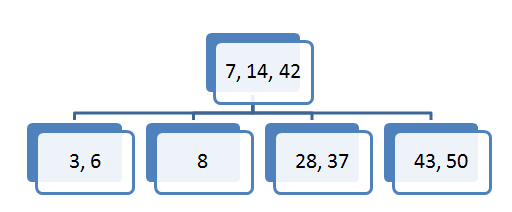
Želen element vstavljamo pri korenu. Poiščemo sina, ki ustreza intervalu elementa, ki ga želimo vstaviti. Če je vozlišče prazno oziroma ima en ali dva elementa v vozlišču element vstavimo. V primeru da vozlišče vsebuje tri elemente velja slednje:

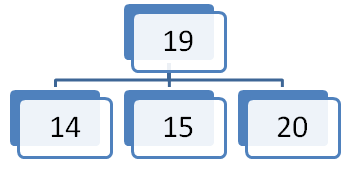
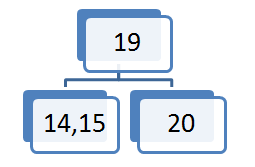
• če je vozlišče KOREN drevesa, sredinski element postane nov koren ostala dva elementa pa razpadeta v dva vozlišča. Prvi postane levi sin drugi pa desni sin z ustreznimi poddrevesi. Višina drevesa se je povečala za ena.
• če vozlišče NI KOREN drevesa, sredinski element vstavimo v očeta trenutnega vozlišča, ostala dva elementa razpadeta v dva vozlišča. V tem primeru se višina drevesa ne poveča.

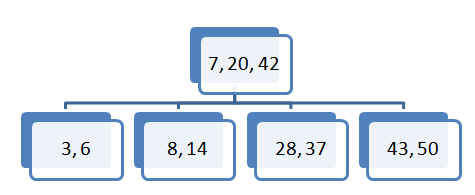
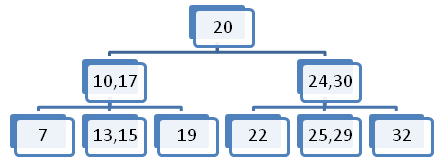
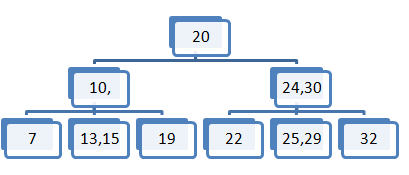
Primer element vstavimo v list 2-3-4 drevesa, kjer se v vozlišču trenutno nahajajo trije elementi

• Sredinski element prestavimo v vozlišče očeta ostala dva razpadeta v dva vozlišča, ki postaneta levi in desni sin. Element ki ga želimo vstaviti, preverimo na katerem intervalu je in ga vstavimo v dano vozlišče.

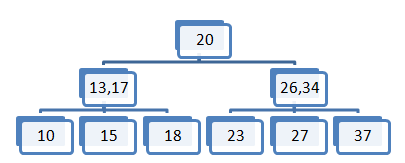
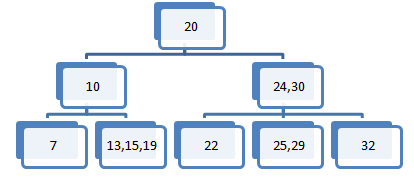
1. V 2-3-4 drevo bomo vstavili element 20.

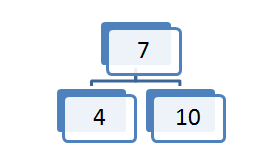
   • Začetno 2-3-4 drevo.

     

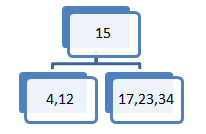
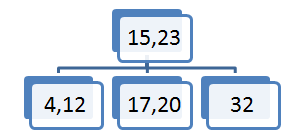
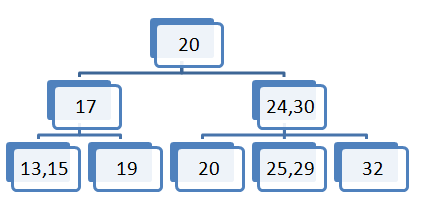
   • Element 20 želimo vstaviti v vozlišče (17,23,34), ker pa vozlišče že vsebuje tri elemente moramo sredinski element (to je 23) prestaviti v vozlišče očeta.

     

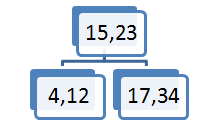
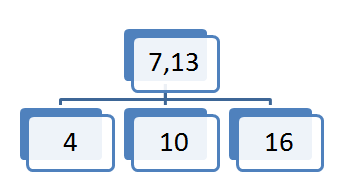
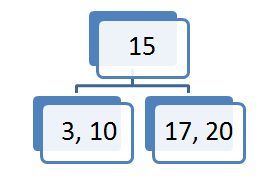
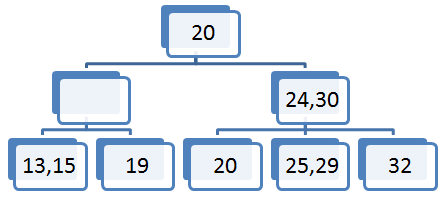
   • S tem ko smo element 23 prestavili v vozlišče očeta, drevo ni več iskalno. V vozlišču očeta sta trenutno dva elementa, kar pomeni da mora imeti oče tri sinove. Tako vozlišče (17,34) razpade na dva vozlišča(17),(34).

     

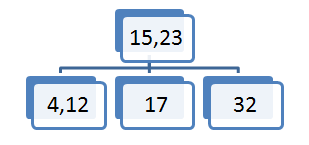
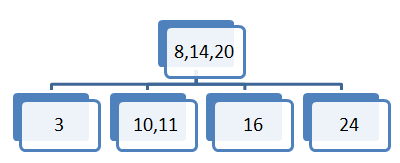
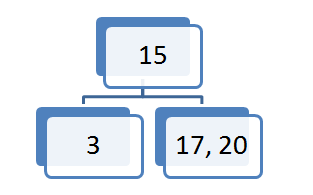
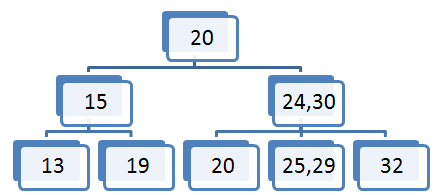
   • Element 20 vstavimo v sredinsko vozlišče saj je 20 večje od elementa 15 in manjše od elementa 23.

     

Primer element vstavimo v 2-3-4 drevo, ko se v vozlišču korena nahajajo trije elementi

• V danem primeru sredinski element postane nov koren drevesa. Višina drevesa se poveča za ena. Ostala dva elementa pa razpadeta v dva nova vozlišča in sicer v levo in desno poddrevo. Za element ki ga želimo vstaviti preverimo na katerem intervalu se nahaja in ga tja tudi vstavimo.

Brisanje v 2-3-4 drevesu je najbolj zahteven postopek. Najprej je potrebno poiskati vozlišče z elementom, ki ga želimo izbrisati.

1. Če se element nahaja v listu drevesa in se v vozlišču nahajata dva ali trije elementi slednjega enostavno izbrišemo. V primeru da je element sam v vozlišču:

   • Preverimo ali ima vsaj en izmed bratov, vsaj dva elementa v vozlišču. V tem primeru željen element izbrišemo, ostane prazno vozlišče. V prazno vozlišče vstavimo element, ki se trenutno nahaja v vozlišču očeta, na očetovo mesto pride element iz vozlišča enega izmed bratov (v katerem sta bila vsaj dva elementa).
   • Noben izmed bratov nima vsaj dveh elementov v vozlišču. V tem primeru željen element izbrišemo, ostane prazno vozlišče. V prazno vozlišče vstavimo element, ki se je trenutno nahajal v vozlišču očeta. Nato pa dano vozlišče združimo z ustreznim bratom.
2. Element se ne nahaja v listu drevesa. V tem primeru ga nadomestimo z maksimalnim elementom levega poddrevesa.

Primer brisanja, ko se element nahaja v listu drevesa.

• Na 2-3-4 drevesu ni večjih sprememb. Izbrišemo element 10.

• 2-3-4 drevo brez elementa 10

  

Primer brisanja, ko ima vsaj en od bratov dva ali tri elemente v vozlišču

• Iz vozlišča drevesa izbrišem element 17, ki se nahaja v desnem listu.

  

• Izbrisali smo element 17, zato desni sin predstavlja prazno vozlišče.

  

• V prazno vozlišče vstavimo element, ki je predstavljal dosedanjega očeta. Na mesto dosedanjega očeta pa vstavimo največji element iz vozlišča levega sina in to je element 13.

  

Primer brisanja, ko noben od bratov nima vsaj dveh elementov v vozlišču

• Iz 2-3-4 drevesa bomo izbrisali element 7.

  

• Izbrisali smo element 7, vozlišče je trenutno prazno.

  

• V prazno vozlišče vstavimo element, ki se nahaja v vozlišču očeta. Sedaj ima vozlišče očeta samo en element, kar pomeni da ima 2-3-4 drevo lahko le dva sinova.

  

• Združili smo vozlišče (14) in vozlišče (15) v eno vozlišče (14,15). Po združitvi vozlišč je 2-3-4 drevo iskalno.

  

Primer brisanja, ko se element nahaja v vozlišču očeta

• Iz 2-3-4 drevesa bomo izbrisali element 20.

  

• Levi sin od elementa 20 je vozlišče (8,14), desni sin pa predstavlja vozlišče (28,37). Element 20 odstranimo iz vozlišča očeta, ki ga bomo nadomestili z maksimalnim elementom levega sina (in to je 14).

  

• Na prazno mesto v vozlišču očeta vstavimo (maksimalen element levega sina od elementa 20) element 14.

  

Primer brisanja, pri čemur se združita brata v listih drevesa

• Iz 2-3-4 drevesa izbrisemo element 17

  

• V vozlišču kjer se nahaja element 17 je še en element, kar pomeni, če odstranimo 17 ima slednje vozlišče lahko le dva sinova. Preverimo vozlišča sinov in jih združimo, glede na pravilni interval.

  

• 2-3-4 drevo z izbrisanim elementom 17.

  

Primer brisanja, ko maksimalen element levega poddrevesa prestavimo na mesto izbrisanega elementa

• Iz 2-3-4 drevesa bomo izbrisali element 17.

  

• Vozlišče iz katerega smo izbrisali element 17, je trenutno prazno. Zato pogledamo elemente v levem simu in največji element prestavimo v prazno vozlišče.

  

• 2-3-4 drevo z izbrisanim elementom 17.

  

//en.wikipedia.org/wiki/2-3-4_tree

//www.dcs.gla.ac.uk/~pat/52233/slides/234Trees1x1.pdf

//www.csse.monash.edu.au/~lloyd/tildeAlgDS/Tree/234tree/

//www.scribd.com/doc/50707583/3/Tree-Example

//wiki.fmf.uni-lj.si/wiki/Intervalno_drevo

//ultrastudio.org/en/2-3-4_tree

//www.nauk.si/materials/5050/out/