Podatki o maturitetni nalogi:

• Splošna matura
  
• Maturitetna pola 5. junij 2010, osnovna raven
  
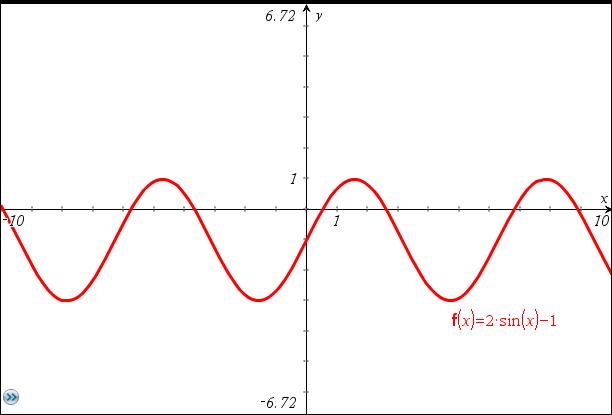
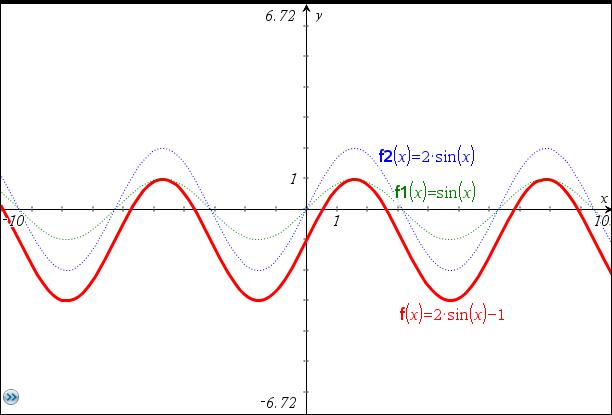
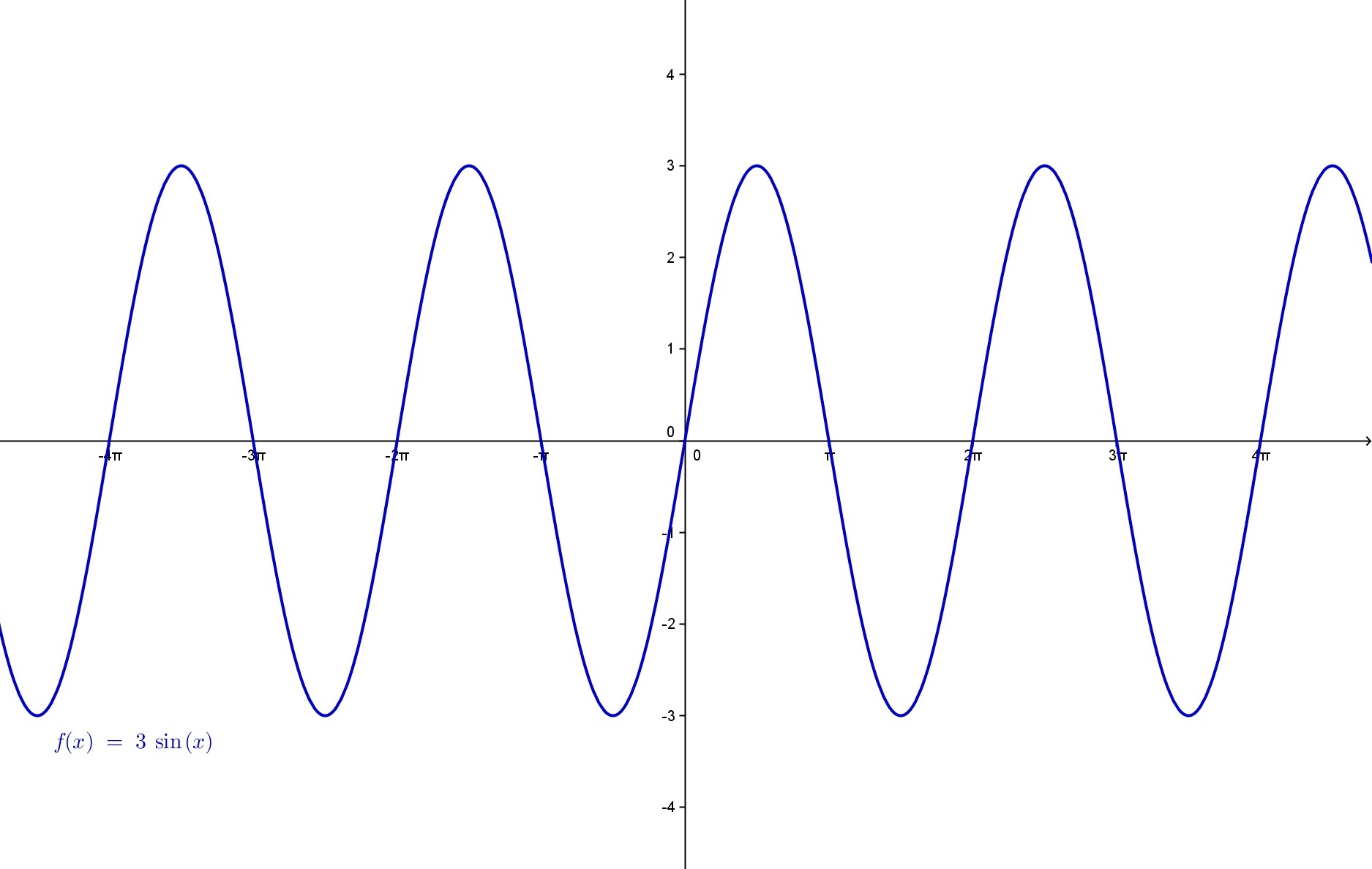
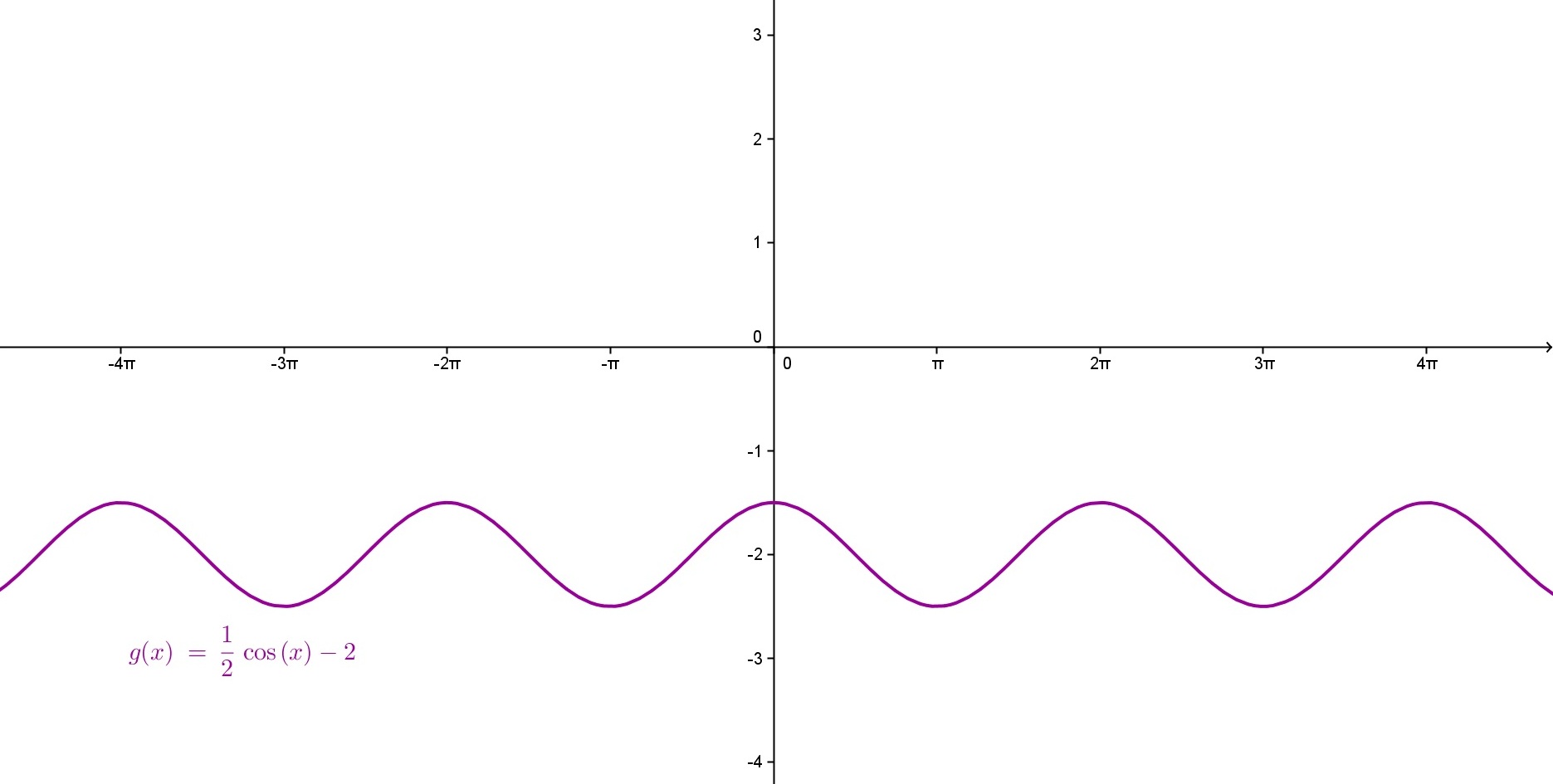
• 5. naloga
  
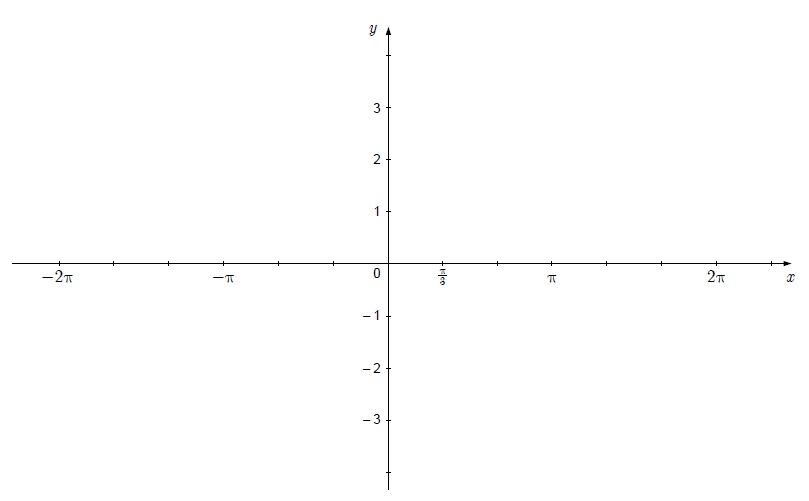
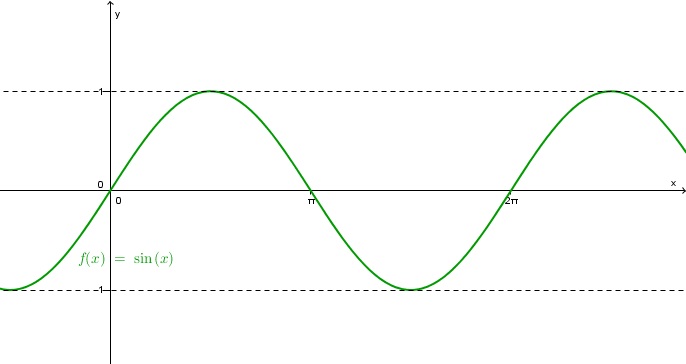
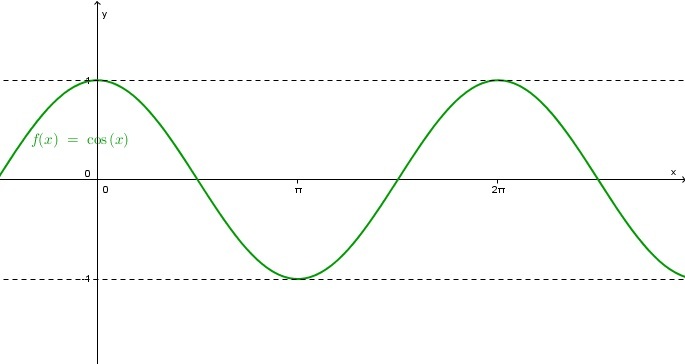
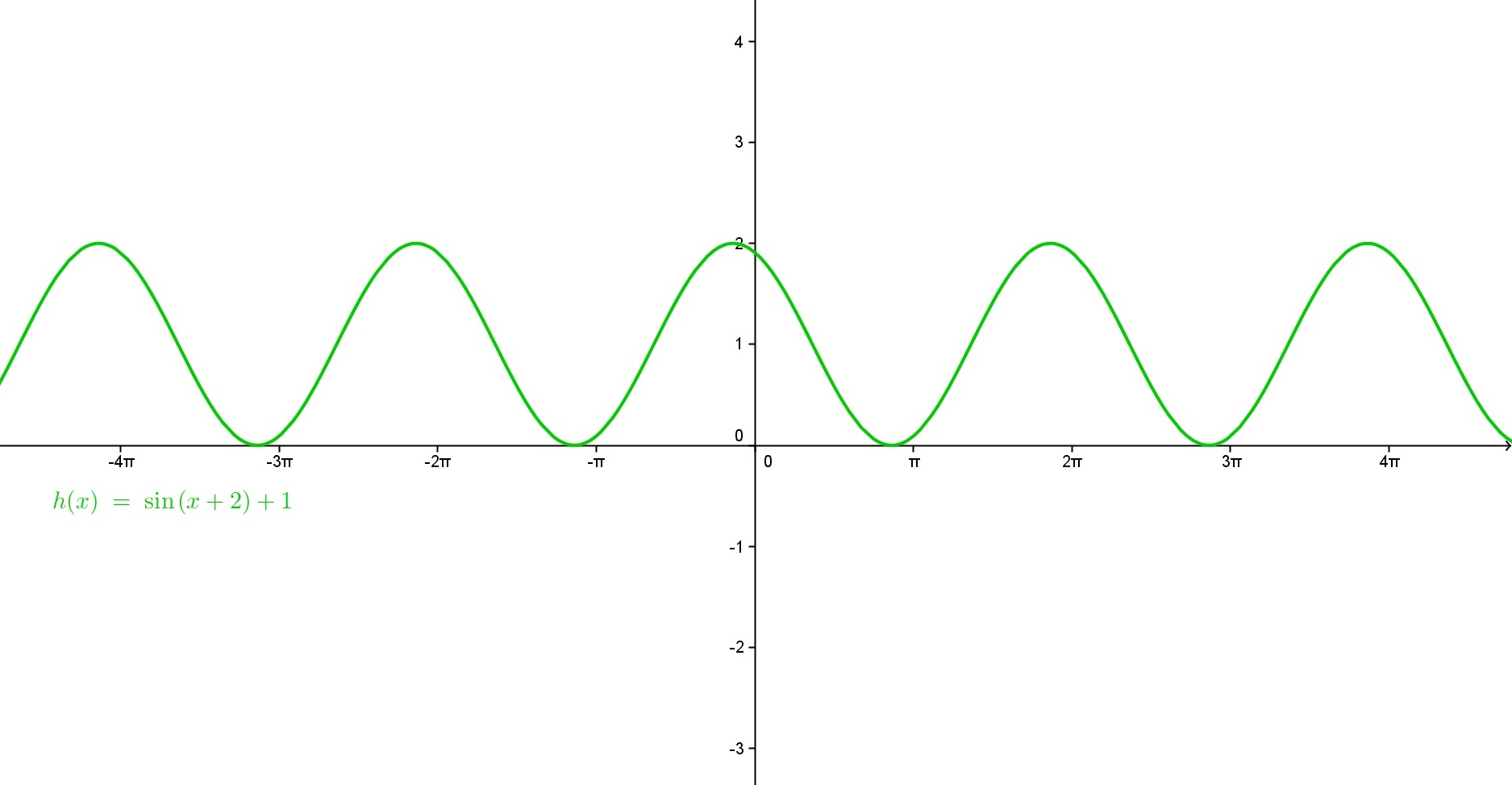
• Snov: trigonometrične funkcije
  

Povezava na maturitetno polo: Klik

Na teh prosojnicah lahko najdemo:

• kratko ponovitev snovi, povezane z maturitetno nalogo
• postopek reševanja naloge s programom Ti-Nspire
• preverjanje znanja - reševanje kviza ali reševanje sorodne naloge

Začni

Dana je funkcija .
Izračunajte ničle te funkcije in narišite njen graf v dani koordinatni sistem.

Ponovitev teorije

Reševanje naloge s pomočjo Ti-Nspire

Sinus in kosinus

Premaknite rdečo točko vzdolž krožnice in opazujte spreminjanje vrednosti sinusa in kosinusa kota v odvisnosti od velikosti kota . Kaj opazite?

Sinus kota je ordinata točke, v kateri drugi krak kota seka enotsko krožnico, kosinus kota pa je abscisa te točke.

Definicijsko območje sinusa in kosinusa je množica realnih števil, saj lahko poljubnemu kotu poiščemo vrednost sinusa in kosinusa. Obe funkciji sta omejeni, dosežeta lahko le vrednosti med –1 in 1. Torej je zaloga vrednosti interval [–1,1].

Sinus je liha, kosinus pa soda funkcija.

Graf funkcije sinus

Sinus je funkcija , kjer . Je periodična funkcija s periodo .

Ničle

Ničle funkcije sinus so rešitve enačbe

Graf funkcije cosinus

Cosinus je funkcija , kjer . Je periodična funkcija s periodo .

Ničle

Ničle funkcije cosinus so rešitve enačbe

Na spodnjih povezavah je na voljo podrobnejša razlaga snovi:

Več o kotnih funkcijah

Reševanje naloge s pomočjo Ti-Nspire

Odpremo nov dokument za geometrijo, v katerem narišemo .

Za pomoč lahko narišemo še pomožna grafa in , saj bi brez uporabe računala do grafa funkcije f(x) najlažje prišli prek risanja omenjenih funkcij.

Za izračun ničel odpremo novo stran z računanje (Calculator).
Ničle lahko izračunamo na dva načina:

1. uporabimo ukaz Solve, ki reši dano enačbo
   

   

   
   

2. ali uporabimo ukaz Zeros, ki za dani izraz poišče ničle.
   

   

   
   

Z obema načinoma dobimo enako rešitev. Pri tem sta in poljubni celi števili.

Spodaj je na voljo še povezava do filmčka s celotnim postopkom reševanja naloge v programu Ti-Nspire CX CAS.

Povezava na filmček

Nekaj nalog

1. naloga

Dana je funkcija

Njenih nekaj ničel je:

Preveri

2. naloga

Na list papirja narišite spodnje funkcije in nato preverite rešitve s klikom na gumb.

• 
  
  Rešitev

  

  
  

• 
  
  Rešitev

  

  
  

• 
  
  Rešitev

  

  
  

Kje funkcija seka y-os?
Koordinato izračunajte na dve decimalki natančno in rešitev zapišite v spodnje okence.

Y-koordinata presečišča krivulje z y-osjo je

Preveri