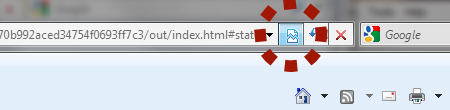
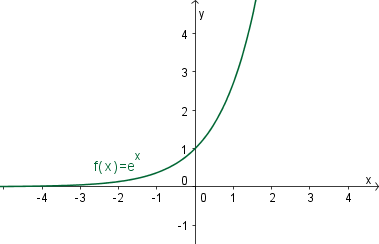
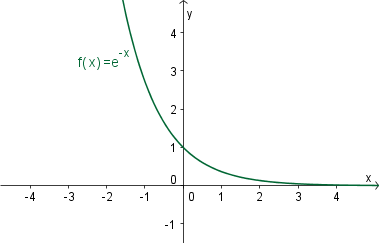
Eksponentna funkcija z osnovo (kjer je in ) je preslikava in je definirana za vsak : .
Eksponentna funkcija - teorija
Eksponentna funkcija - teorija
Skupina NAUK
Razumevanje eksponentne odvisnosti in lastnosti eksponentne funkcije, risanje grafa eksponentne funkcije ter reševanje eksponentnih enačb.
Definicija eksponentne funkcije
Zaloga vrednosti
Zaloga vrednosti eksponentne funkcije so vsa pozitivna realna števila: .
Pri ima eksponentna funkcija vrednost 1, ker . Na grafu dobimo premico .
Za je funkcija padajoča, za je funkcija strogo naraščajoča.
Lastnosti eksponentne funkcije
Funkcija ima naslednje lastnosti:
- Zaloga vrednosti so vsa pozitivna naravna števila: .
- .
- Če je , potem je .
- Za je funkcija padajoča, za je funkcija naraščajoča.
- Abscisna os je vodoravna asimptota.
Inverzna funkcija k eksponentni funkciji je logaritemska funkcija.
Graf eksponentne funkcije
Graf eksponentne funkcije je krivulja z enačbo . Z upoštevanjem lastnosti eksponentne funkcije rešimo naslednja dva zgleda.
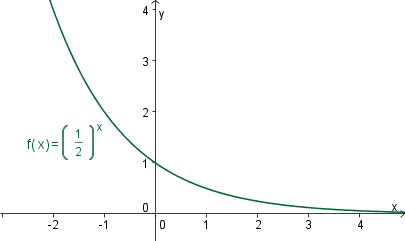
Zgled: Narišite graf funkcije .
Rešitev:
Funkcijo preoblikujemo .
Vemo, da je funkcija povsod pozitivna in da je . Ker je , torej je funkcija padajoča.
Zapišemo še nekaj funkcijskih vrednosti in narišemo funkcijo.
|
Graf eksponentne funkcije
Zgled: Dana je funkcija .
a.) Poiščite presečišči funkcije s koordinatnima osema.
b.) Določite asimptoto grafa funkcije.
c.) Narišite graf dane funkcije.
Rešitev:
a.) Presečišča funkcije s koordinatnima osema:
| : | : | |||
Dobimo presečišči in .
b.) Asimptota grafa funkcije je .
c.) Graf dane eksponentne funkcije lahko že narišemo iz izračunanih podatkov. Lahko pa tudi izračunamo še nekaj funkcijskih vrednosti.
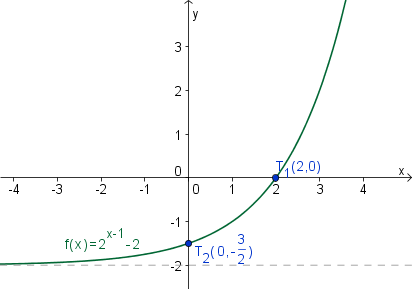
Vodoravna asimptota funkcije je . V nalogi je podana funkcija . Število pomeni, da smo celotno funkcijo na grafu premaknili za 2 navzdol. To pomeni, da se je premaknila tudi asimptota, zato je asimptota danega grafa .
Razteg grafa eksponentne funkcije
Grafa funkcije in sta zrcalna glede na ordinatno os.
Premik grafa eksponentne funkcije
Eksponentna funkcija z osnovo
Eksponentna funkcija z osnovo je poseben primer eksponentne funkcije: , kjer je
.
|
|
Eksponentne enačbe
V eksponentni enačbi nastopa neznanka v eksponentu. Pri reševanju eksponentnih enačb si pomagamo tako, da vse člene enačbe prevedemo na isto osnovo: . Enakost velja, če je .
Ponovimo lastnosti računanja s potencami, kjer sta in :
1.
2.
3.
4.
5.
6. , ,
Zgledi eksponentnih enačb
Zgled: Rešite enačbo .
Rešitev:
Prevedemo vse člene enačbe na isto osnovo:
Izenačimo eksponente:
Enačba ima dve rešitvi:
in
Zgledi eksponentnih enačb
Zgled: Rešite enačbo .
Rešitev:
Izpostavimo skupni faktor:
Enačaj bo veljal v primeru, ko bosta eksponenta enaka nič (), torej:
Radioaktivni razpad
Pri radioaktivnosti uporabljamo eksponentno enačbo za opis odvisnosti števila radioaktivnih jeder v vzorcu od časa:
kjer je razpadna konstanta, razpadni čas in število jeder ob času in .
Vidimo, da število radioaktivnih jeder v vzorcu s časom eksponentno pada. Poskusimo rešiti konkretno nalogo.
Naloga: Razpadna konstanta za je . V kakšnem času razpade polovica ?
