AA drevsa so preprosta oblika uravnoteženih iskalnih dvojiških dreves. Zgrajena so zelo podobno kot rdeče črna drevesa, le da potrebujemo pri AA drevesih bistveno manj operacij za ohranjanje uravnoteženosti drevesa (npr. AA drevo pozna 2 taki operaciji, rdeče črno drevo pa kar 7). AA drevesa so dobila ime po njihovem izumitelju Arne Anderssonu.

Torej prednosti AA dreves so:

• Veliko število standardnih operacij za ohranjanje uravnoteženosti iskalnih dvojiških dreves zamenjamo z dvema enostavnima operacijama
• Implementacija te strukture je zelo preprosta
• Brisanje poljubnega vozla je bistveno bolj enostavno kot pri drugih podobnih podatkovnih strukturah

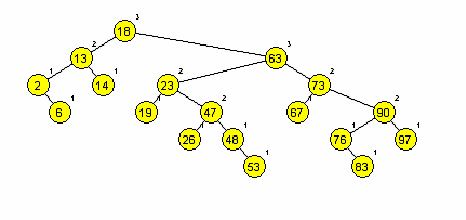
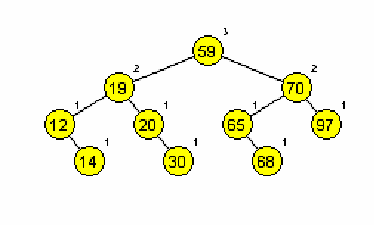
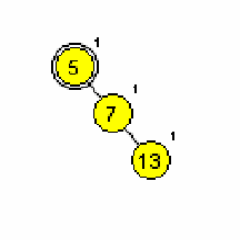
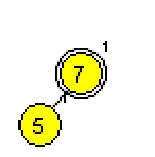
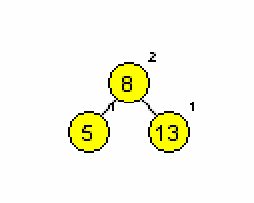
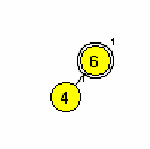
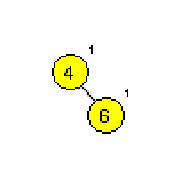
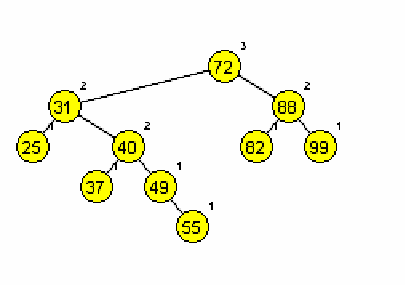
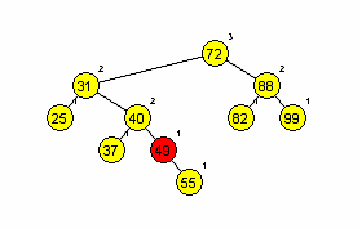
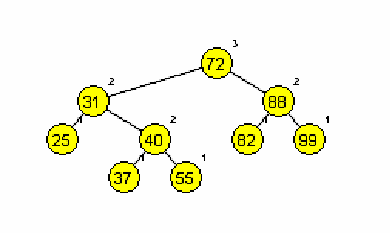
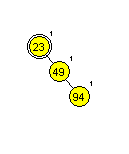
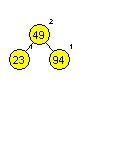
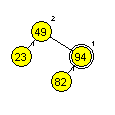
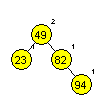
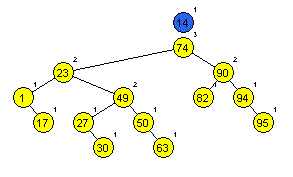
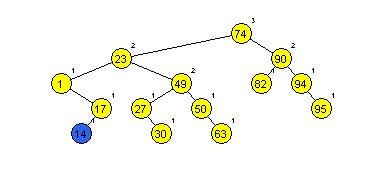
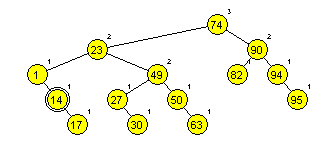
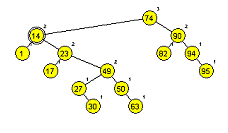
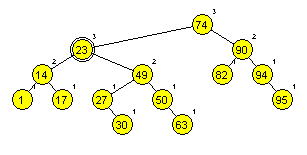
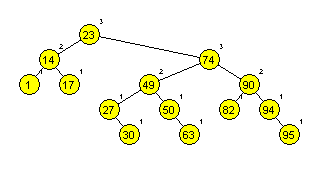
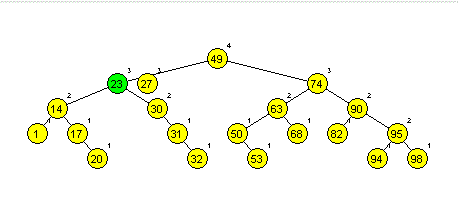
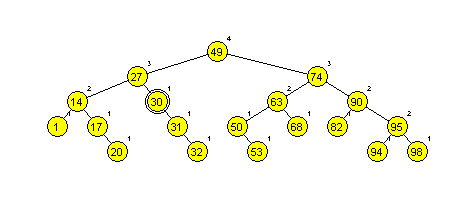
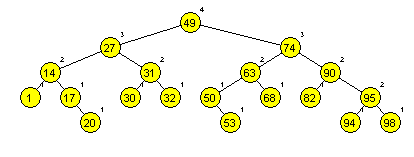
Primera AA dreves (slika 1 in 2):

Slika 1

Slika 2

Uravnoteženo drevo je tako dvojiško drevo, v katerem se globini levega in desnega poddrevesa vsakega vozlišča razlikujeta kvečjemu za 1. k-uravnoteženo drevo je tako dvojiško drevo, v katerem se globini levega in desnega poddrevesa vsakega vozlišča razlikujeta kvečjemu za k.

Slika 3: Neuravnoteženo drevo

Slika 4: Uravnoteženo drevo

Povzeto po: Uravnoteženo drevo

AA drevesa so definirana malo drugače kot ostala drevesa. Pomembno vlogo pri AA drevesih ima stopnja vozlišča

Lastnosti AA dreves:

• Stopnja lista je vedno enaka 1
• Stopnja levega otroka je vedno strogo manjša od stopnje njegovega očeta
• Stopnja desnega otroka je manjša ali enaka stopnji njegovega očeta.
• Stopnja desnega vnuka je vedno strogo manjša od stopnje njegovega dedka.
• Vsako vozlišče ki ima dva otroka, ima stopnjo strogo večjo kot 1.

slika 5

Slika 5 prikazuje vozlišče s podatkom(7) in njegovo stopnjo(1).

Povezavi kjer imata oče in sin isto stopnjo pravimo horizontalna povezava.

Leva horizontalna povezava je povezava kjer imata levi sin in oče isto stopnjo.

Desna horizontalna povezava je povezava kjer imata desni sin in oče isto stopnjo.

Leva horizontalna povezava je prepovedana - zaradi točke 2.

Dvojna desna horizontalna povezava je prepovedana - točka 4.

Sliki 6 in 7 prikazujeta horizontalni povezavi.

Slika 6: Dvojna desna horizontalna povezava

Slika 7: Leva horizontalna povezava

Dvojna horizontalna povezava je povezava, kjer imajo dedek, oče in sin isto stopnjo

Ko dodajamo ali brišemo vozlišča v AA drevesih pogosto pride do dvojnih horizontalnih povezav ali pa do leve horizontalne povezave, kar ne ustreza našim pravilom. Zato za ohranitev uravnoteženosti uporabljamo 2 operaciji:

1. Leva rotacija (split)
2. Desna rotacija (skew)

Slika 8

Slika 8 prikazuje nepravilno grajeno AA drevo. Elementi 70, 89 in 93 tvorijo dvojno horizontalno povezavo. Dvojno desno horizontalno povezavo rešujemo s pomočjo leve rotacije.

Levo rotacijo(split) torej uporabimo takrat, ko zaradi vstavljanja ali brisanja vozlišča v drevesu nastane dvojna desna horizontalna povezava. Za zgled si poglejmo enostavno drevo z dvojno desno horizontalno povezavo (slika 9).

Slika 9

Slika 10

Levo rotacijo izvršimo tako, da vmesnemu vozlu povečamo stopnjo za 1 in ga postavimo na mesto očeta. Na mesto levega sina postavimo njegovega prejšnjega očeta, desni sin pa ostane isti. Dobimo drevo, ki je na sliki 10. To drevo zdaj ustreza vsem pogojem AA dreves.

Desno rotacijo(skew) uporabljamo, ko zaradi vstavljanja ali brisanja vozlišča v drevesu nastane leva horizontalna povezava (slika 11).

Slika 11

Slika 12

Desno rotacijo izvršimo tako, da levega sina postavimo na mesto očeta, očeta pa postavimo na mesto desnega sina novega očeta. Dobimo drevo, ki je na sliki 12.

Brisanje vozlišča v AA drevesu je zelo preprosto. Za primer si bomo izbrali drevo s slike 13.

Recimo da želimo zbrisati vozlišče 49. Vozlišče je treba najprej poiskati. Ker vemo da je AA drevo iskalno drevo, so vsi podatki v levem poddrevesu manjši od korena, vsi podatki v desnem poddrevesu pa večji od korena. Torej z iskanjem začnemo pri korenu. V našem primeru je koren vozlišče s podatkom 72. Vemo, da se vozlišče s podatkom 49 nahaja v levem poddrevesu, ker je 49 manjše od 72. Torej nadaljujemo pot v levo poddrevo.

Slika 13

Slika 14

Našli smo vozlišče, ki ga želimo izbrisati(Slika 14, rdeče vozlišče). Zdaj izberemo vozlišče, ki je v desnem poddrevesu od vozlišča 49 najbolj levo. To je vozlišče 55. Torej vozlišče 55 bo nadomestilo naše vozlišče 49.

Zdaj moramo preveriti, če je novo drevo (slika 15) ki smo ga dobili, res AA drevo.

Slika 15

Začnemo pri tistemu vozlišču, ki je nadomestilo naše izbrisano vozlišče (v našem primeru vozlišče 55). Nato preverimo, če na tej točki izpolnjujemo vseh 5 lastnosti AA dreves. Če jih izpolnjujemo, nadaljujemo pot proti korenu.

Naslednje vozlišče je vozlišče 40. Tudi tu moramo preveriti, če drevo ustreza pravilom AA drevesa. Ustreza, nadaljujemo pot do korena. Naslednje vozlišče je 31. Tudi to ustreza lastnostim AA drevesa. Naslednje vozlišče je koren in tudi tu izpolnjujemo vsa pravila AA dreves. Zdaj vemo, da slika 15 res prikazuje AA drevo.

Po vrsti bomo vstavljali vozlišča: 49, 94, 23, 82, 1, 90, 74, 50, 27, 17, 30, 63, 95, 14, 74, 68, 32, 31, 98, 53, 20. Nato pa bomo odstranili vozlišče 23.

Vozlišče 49 je prvo v drevesu in dobi stopnjo 1(slika 16). Vozlišče 94 je večje kot 49, zato ga vstavimo v desno poddrevo in dobi stopnjo 1 (slika 17).

Slika 16

Slika 17

Vozlišče 23 je manjše kot 49, zato ga vstavimo v levo poddrevo in dobi stopnjo 1 (slika 18). Ker ima enako stopnjo kot njegov oče pomeni, da imamo levo horizontalno povezavo, ki ni dovoljena v AA drevesih, zato moramo izvesti desno rotacijo (slika 19).Preverimo, če drevo ustreza lastnostim AA dreves. Ne ustreza, ker imamo zdaj dvojno desno horizontalno povezavo. Torej moramo izvesti levo rotacijo (slika 20).

Slika 18

Slika 19

Slika 20

Ponovno preverimo, če drevo ustreza lastnostim AA dreves. Ustreza, gremo naprej!

Naslednje vozlišče je 82. Ker je večje kot koren, nadaljujemo pot v desno poddrevo. Zdaj primerjamo z vozliščem 94. Ker je 82 manjše od vozlišča 94, gremo v levo poddrevo. Vozlišče postane levi sin vozlišča 94 in dobi stopnjo 1 (slika 21). Ker ima enako stopnjo kot njegov oče (vozlišče 94), imamo levo horizontalno povezavo. Izvesti moramo desno rotacijo (slika 22).

Slika 21

Slika 22: Drevo po desni rotaciji

Preverimo, če drevo ustreza lastnostim AA dreves. Ustreza, postopek nadaljujemo!

Do sedaj smo vstavili vozlišča: 49, 94, 23, 82, 1, 90, 74, 50, 27, 17, 30, 63, 95. Sedaj vstavljamo vozlišče 14 (Slika 23).

Slika 23

Naš koren je sedaj vozlišče 74. Ker je 14 manjše od 74, nadaljujemo pot v levo poddrevo. Pridemo do naslednjega vozlišča 23. Ker je 14 manjše od 23, nadaljujemo pot v levo poddrevo. Pridemo do vozlišča 1, ker je 14 večje kot 1, nadaljujemo pot v desno poddrevo. Pridemo do vozlišča 17, ker je 14 manjše kot 17, gremo v levo poddrevo.

Slika 24

Slika 25: drevo po desni rotaciji

Vozlišče 14 je sedaj levi sin vozlišča 17 in ima stopnjo 1 (slika 24). Spet imamo levo horizontalno povezavo, zato izvedemo desno rotacijo(Slika 25).

Ko izvedemo desno rotacijo ugotovimo, da imamo zdaj dvojno desno horizontalno povezavo(Slika 25). Zdaj moramo izvesti levo rotacijo. Vozlišču 14 povečamo stopnjo za 1, ker ima oba sinova(slika 26). Spet ugotovimo da imamo levo horizontalno povezavo(vozlišča 14 in 23 na sliki 26). Ponovno moramo izvesti desno rotacijo. Ko izvedemo desno rotacijo, vozlišče 14 izgubi svojega desnega sina-vozlišče 17. Njegov novi desni sin je vozlišče 23, ki je bil prej njegov oče. Vozlišče 17 bo zdaj levi sin vozlišča 23(slika 27).

Slika 26: drevo po levi rotaciji

Slika 27: drevo po desni rotaciji

Spet ugotovimo, da imamo dvojno desno horizontalno povezavo(vozlišča 14, 23, 49 na sliki 27), zato ponovno izvedemo levo rotacijo. Stopnjo vozlišča 23 povečamo za 1, njegov novi levi sin je vozlišče 14, vozlišče 17 pa gre na mesto desnega sina vozlišča 14. Vozlišče 23 ima zdaj stopnjo 3(slika 28).

Slika 28

Ponovno imamo levo horizontalno povezavo(vozlišči 23 in koren 74, oba s stopnjo 3). Izvedemo desno rotacijo. Vozlišče 23 postane koren, vozlišče 74 pa njegov desni sin. Vozlišče 74 dobi tudi novega levega sina-vozlišče 49(slika 29).

Slika 29

Preverimo če drevo ustreza lastnostim AA dreves. Ustreza, gremo naprej!

Slika 30

Zdaj vstavljamo vozlišče 74. Primerjamo ga s korenom. Ker je 74 večje od 23, nadaljujemo pot v desno poddrevo(slika 30). Pridemo do vozlišča 74. Ker to vozlišče že nastopa v našem drevesu, ga ne moremo vstaviti. Drevo ostane nespremenjeno.

Slika 31

Na koncu naše AA drevo zgleda kot na sliki 31. Zdaj bomo iz našega drevesa zbrisali vozlišče 23.

Slika 32

Najprej ga poiščemo. Ko smo našli naše vozlišče(slika 32) preverimo, katero vozlišče je najbolj levo v njegovem desnem poddrevesu. To je vozlišče 27. Vozlišče 27 bo nadomestilo naše vozlišče 23. Ker vozlišče 30 nima več 2 sinov, izgubi 1 stopnjo(slika 33).

Slika 33

Preverimo, če naše drevo ustreza lastnostim AA dreves. Ne ustreza, ker imamo dvojno desno horizontalno povezavo(vozlišča 30,31,32). Izvedemo levo rotacijo, vozlišče 31 dobi stopnjo 2, ker ima 2 sina(Slika 34).

Slika 34

Ponovno preverimo če drevo ustreza lastnostim AA dreves. Ustreza, to je torej naše končno AA drevo.

Drugi primer je prikazan v obliki filmčka. Sestavili bomo AA drevo z 20 vozlišči, nato pa bomo zbrisali vozlišče 7.