Potenčna in korenska funkcija - teorija
Potenčna in korenska funkcija - teorija
K.E., Skupina NAUK
Razumevanje potenčne odvisnosti, risanje grafa potenčne funkcije, obravnavanje korenske funkcije kot inverzne funkcije k potenčni funkciji.
Definicija potenčne funkcije z naravnim eksponentom
Definicija potenčne funkcije z negativnim celim eksponentom
Potenčna funkcija z negativnim celim eksponentom je definirana s predpisom , kjer je . Abscisna os je asimptota, ordinatna os je pol.
Funkcija ni definirana za .
Pol ali navpična asimptota funkcije je število , kjer funkcija ni definirana, v okolici tega števila pa vrednosti funkcije naraščajo proti ali padajo proti .
Lastnosti potenčne funkcije z negativnim celim eksponentom
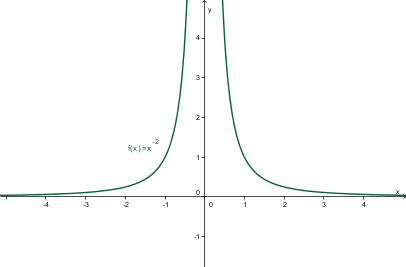
Zgled: Naj bo sodo število . Oglejmo si lastnosti funkcije :
- definicijsko območje funkcije je ,
- zaloga vrednosti funkcije je ,
- je soda,
- naraščajoča je na intervalu ,
- padajoča je na intervalu ,
- abscisna os je asimptota, ordinatna os je pol.
Lastnosti potenčne funkcije z negativnim celim eksponentom
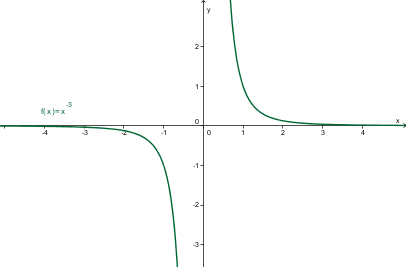
Zgled:Naj bo liho število . Oglejmo si lastnosti funkcije :
- definicijsko območje funkcije je ,
- zaloga vrednosti funkcije je ,
- je liha,
- padajoča je na intervalu ,
- naraščajoča je na intervalu ,
- abscisna os je asimptota, ordinatna os je pol.
Potenčna funkcija je definirana s predpisom , kjer je naravno število.
Potenčne funkcije s sodim eksponentom so sode, njihov graf je simetričen glede na ordinatno os. Potenčne funkcije z lihim eksponentom so lihe, njihov graf je simetričen glede na koordinatno izhodišče.
Definicijsko območje
Definicijsko območje potenčne funkcije z naravnim eksponentom so vsa realna števila.
Za dobimo premico z enačbo .
Za dobimo , torej simetralo lihih kvadrantov.
Lastnosti potenčne funkcije
Zgled: Naj bo sodo število . Oglejmo si lastnosti funkcije :
- je soda, ker zadošča pogoju ,
- zaloga vrednosti funkcije je ,
- padajoča je na intervalu ,
- naraščajoča je na intervalu ,
- funkcija ima minimum v točki T(0,0).
Soda funkcija mora zadoščati pogoju .
Preverimo tako, da vstavimo v funkcijski predpis: . Dana funkcija zadošča pogoju, torej je soda.
Lastnosti potenčne funkcije
Zgled: Naj bo liho število . Oglejmo si lastnosti funkcije :
- je liha, ker zadošča pogoju ,
- zaloga vrednosti funkcije je ,
- naraščajoča je na intervalu ,
- funkcija ima prevoj v točki T(0,0).
Liha funkcija mora zadoščati pogoju .
Preverimo tako, da vstavimo v funkcijski predpis: . Dana funkcija zadošča pogoju, torej je liha.
Prevoj je točka na grafu funkcije, kjer se spremeni smer ukrivljenosti grafa.
Definicija potenčne funkcije z negativnim celim eksponentom
Potenčna funkcija z negativnim celim eksponentom je definirana s predpisom , kjer je . Abscisna os je asimptota, ordinatna os je pol.
Funkcija ni definirana za .
Pol ali navpična asimptota funkcije je število , kjer funkcija ni definirana, v okolici tega števila pa vrednosti funkcije naraščajo proti ali padajo proti .
Lastnosti potenčne funkcije z negativnim celim eksponentom
Zgled: Naj bo sodo število . Oglejmo si lastnosti funkcije :
- definicijsko območje funkcije je ,
- zaloga vrednosti funkcije je ,
- je soda,
- naraščajoča je na intervalu ,
- padajoča je na intervalu ,
- abscisna os je asimptota, ordinatna os je pol.
Lastnosti potenčne funkcije z negativnim celim eksponentom
Zgled:Naj bo liho število . Oglejmo si lastnosti funkcije :
- definicijsko območje funkcije je ,
- zaloga vrednosti funkcije je ,
- je liha,
- padajoča je na intervalu ,
- naraščajoča je na intervalu ,
- abscisna os je asimptota, ordinatna os je pol.
Premiki in raztegi grafov funkcij
Definirajmo funkcijo kot , kjer je .
Graf funkcije dobimo tako, da graf funkcije togo premaknemo za vzdolž ordinatne osi navzgor () oz. navzdol ().
Premiki in raztegi grafov funkcij
Naj bo funkcija definirana kot , kjer je .
Graf funkcije dobimo tako, da graf funkcije togo premaknemo za vzdolž abscisne osi v desno () oz. levo ().
Premiki in raztegi grafov funkcij
Definirajmo funkcijo kot , kjer je .
Graf funkcije dobimo tako, da graf funkcije :
- skrčimo za faktor vzdolž ordinatne osi, če je ,
- raztegnemo za faktor vzdolž ordinatne osi, če je ,
- zrcalimo čez abscisno os in skrčimo za vzdolž ordinatne osi, če je ,
zrcalimo čez abscisno os in raztegnemo za vzdolž ordinatne osi, če je .
Premiki in raztegi grafov funkcij
Definirajmo funkcijo kot , kjer je .
Graf funkcije dobimo tako, da graf funkcije raztegnemo oziroma skrčimo vzdolž abscisne osi. Funkcija doseže enako vrednost kot funkcija pri -krat manjši abscisi .
Definicija in lastnosti korenske funkcije
Korensko funkcijo definiramo kot inverz potenčne funkcije. Njen predpis lahko zapišemo kot , kjer sta in ter .
Za korenska funkcija ni definirana.
Graf inverzne funkcije
Inverzno funkcijo dane funkcije poiščemo tako, da v funkcijskem predpisu med seboj zamenjamo odvisno () in neodvisno () spremenljivko.
Graf inverzne funkcije narišemo tako, da dano funkcijo zrcalimo preko simetrale lihih kvadrantov.
Zgled: Dana je funkcija . Narišite graf dane funkcije in njene inverzne funkcije.
Rešitev:
Najprej narišemo graf funkcije .
Zapišemo inverzno funkcijo ter izrazimo . Dobimo: in narišemo graf.
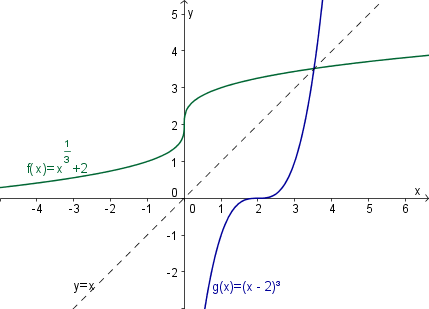
Inverzna funkcija funkcije obstaja le, če je bijektivna funkcija. In obratno: če je bijektivna, ima vedno inverzno funkcijo.
- Definicija potenčne funkcije z naravnim eksponentom
- Definicija potenčne funkcije z negativnim celim eksponentom
- Lastnosti potenčne funkcije z negativnim celim eksponentom
- Lastnosti potenčne funkcije
- Definicija potenčne funkcije z negativnim celim eksponentom
- Lastnosti potenčne funkcije z negativnim celim eksponentom
- Premiki in raztegi grafov funkcij
- Definicija in lastnosti korenske funkcije
- Graf inverzne funkcije
