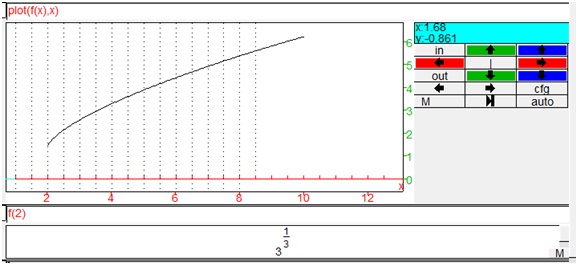
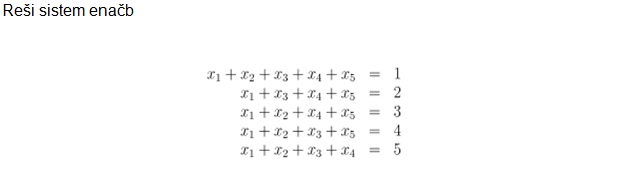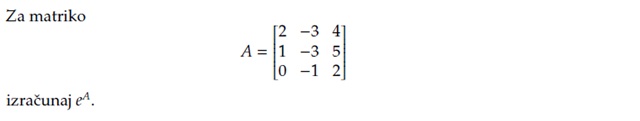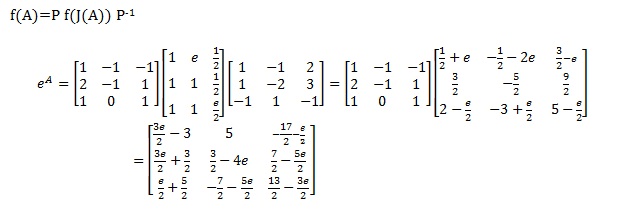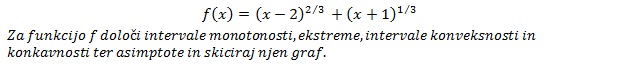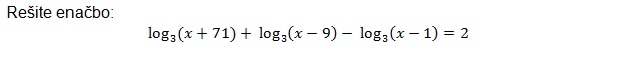Besedilo naloge
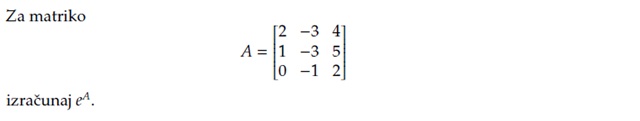
- Rešitev
Z Octave-om poiščemo lastne vrednosti matrike A:
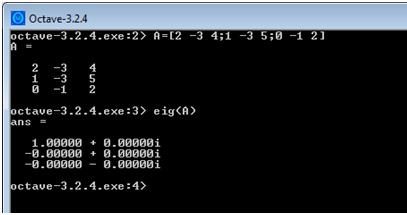
Vidimo, da ima matrika eno enojno (𝜆 = 1) ter dvojno ničlo (𝜆 = 0).
Izračunajmo matriko A-I ter določimo njen rang:
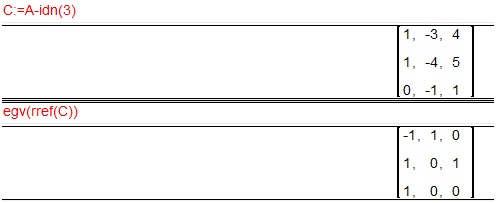
Določimo rang matrike A oz. matrike A - 0×I ter matriko A^2:
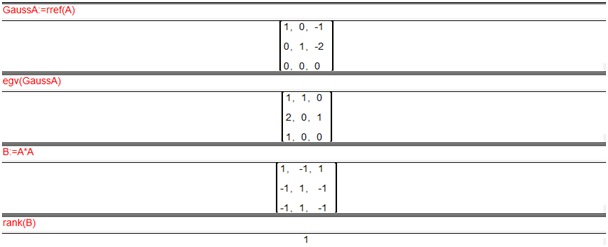
Da bi določili prehodno matriko, je potrebno izračunati jedra matrik A-1×I, A ter A^2:
A-I ⟹ (-1, 1, 1)
A ⟹ (1, 2, 1)
A^2 ⟹ (-1, -1, 0)

Torej je prehodna matrika P:
Z orodjem izračunamo inverz prehodne matrike:
Zdaj je potrebno določiti še Jordanovo formo za našo matriko A:
Zaradi rangov matrik A-I ter A, imamo kletki velikosti 1×1 in 2×2:
Preverimo, če je A=PJP^{-1}:
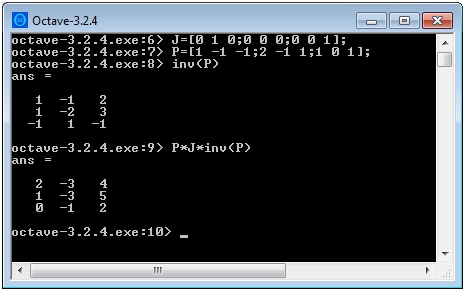
Po preizkusu vidimo, da sta Jordanova forma ter prehodna matrika prav določeni.
Torej:
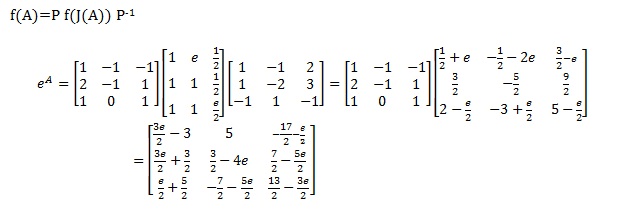
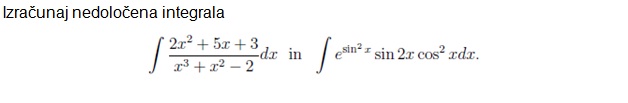
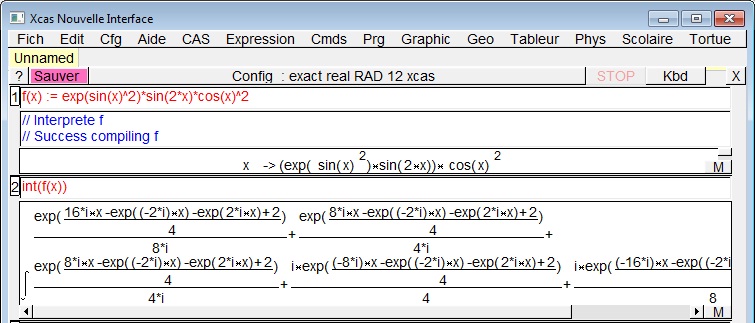
 b) Pri tem primeru, nam pa program vrne čudne vrednosti.
b) Pri tem primeru, nam pa program vrne čudne vrednosti.




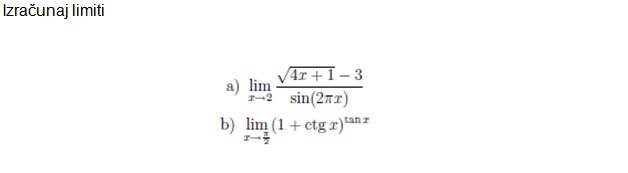
 b)
b)