Pri definiciji korenov poljubnih stopenj smo ločili dva primera; kadar je eksponent liho oziroma sodo naravno število. Ob reševanju nalog bomo ponovili lastnosti korenov.
Izračunaj in svojo rešitev utemelji.
a) = | b) = | |||||
c) = | d) = |
| Preveri |
Korenska funkcija
Korenska funkcija
E-um, K. E.(vsebinsko), Skupina NAUK (tehnično)
Ponovitev o korenih: Naloga 1
Pravilno
Na vsa vprašanja si odgovoril pravilno.
Napačno
Nekateri tvoji odgovori so lahko pravilni, vendar ne vsi. Poskusi še enkrat.
Ponovitev o korenih: Naloga 2
Pravilno
Na vsa vprašanja si odgovoril pravilno.
Napačno
Nekateri tvoji odgovori so lahko pravilni, vendar ne vsi. Poskusi še enkrat.
Pri korenih sodih stopenj moramo paziti na to, da je korenjenec nenegativno število.
Ko je pri enačbah oblike sodo število in , obstajata dve (nasprotni si) rešitvi; ko je liho število, je rešitev ena sama.
Povzetek ponovitve o korenih
Če povzamemo:
- kadar je sodo naravno število in nenegativno realno število, potem je natanko tedaj, ko je ;
- kadar je liho naravno število in poljubno realno število, potem je natanko tedaj, ko je .
Ker so koreni lihih stopenj definirani za vsa realna števila, se bomo najprej seznanili s korenskimi funkcijami z lihim eksponentom.
Korenske funkcije z lihim korenskim eksponentom
Dano imaš potenčno funkcijo s predpisom .
1. Med spodaj naštetimi lastnostmi označi tiste, ki jih ta funkcija ima.
| Preveri |
| Utemeljitev rešitve |
| Graf funkcije |
Zapiši predpis in poskušaj narisati graf njene inverzne funkcije, če jo ima.
| Rešitev |
Pravilno
Tvoj odgovor je pravilen.
Napačno
Tvoj odgovor je napačen. Poskusi še enkrat.
Funkcija je naraščajoča, saj se z večanjem vrednosti spremenljivke veča tudi funkcijska vrednost.
Funkcija je neomejena, saj je njena množica slik množica vseh realnih števil.
Funkcija je liha in ne soda, saj za lihe funkcije velja , kar za funkcijo velja.
Funkcija je bijektivna, saj najdemo za vsak natančno en ustrezen , za katerega velja, da je .
Ker je funkcija bijektivna, ima inverzno funkcijo.
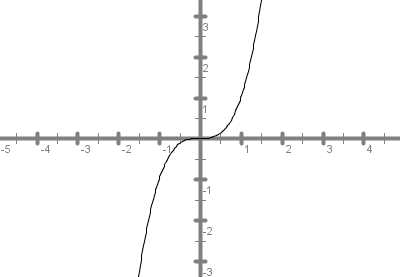
Na grafu funkcije so lepo vidne njene lastnosti: je naraščajoča, neomejena, liha (graf je zrcalen glede na koordinatno izhodišče) in bijektivna, saj poljubna vzporednica z abscisno osjo seka graf natanko enkrat.
Predpis inverzne funkcije poiščemo tako, da zamenjamo vlogi spremenljivk. Po zamenjavi dobimo:
Po definiciji korena lihe stopnje je natanko tedaj, ko je . Povedano drugače: da se znebimo tretje potence, obe strani enačbe korenimo s tretjim korenom.
Torej je predpis inverzne funkcije .
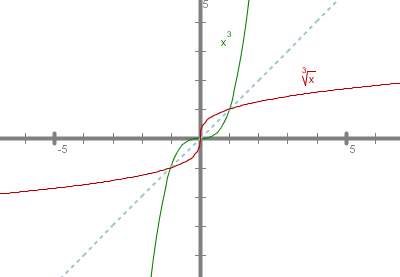
Graf inverzne funkcije dobimo z zrcaljenjem grafa funkcije preko simetrale lihih kvadrantov. Na grafu vidimo, da je inverzna funkcija , naraščajoča, liha, neomejena in bijektivna.
Grafi in lastnosti korenskih funkcij z lihim korenskim eksponentom
Grafi korenskih funkcij z lihim korenskim eksponentom
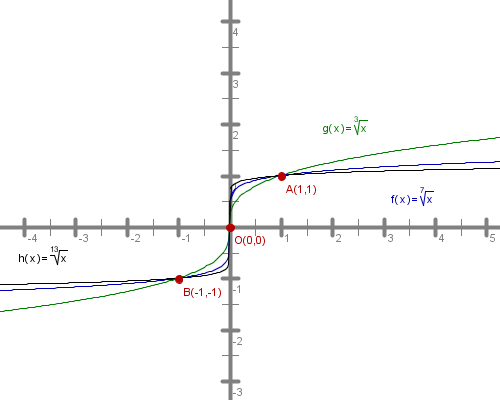
Slika nam prikazuje grafe korenskih funkcij z različnimi lihimi korenskimi eksponenti. Opazimo, da imajo podobno obliko, ki se razlikuje po strmini, in potekajo skozi tri skupne točke.
Glavne lastnosti korenskih funkcij z lihim korenskim eksponentom:
- in
- naraščajoče na celotnem definicijskem območju,
- so lihe,
- so bijektivne,
- imajo tri skupne točke , in ,
- so neomejene.
Naloga 1
1. Zapiši inverzno funkcijo funkcije .
| Rešitev |
2. Nariši graf funkcije ) in v isti koordinatni sistem.
| Graf funkcij |
3. Nariši graf funkcije .
| Namig |
| Rešitev |
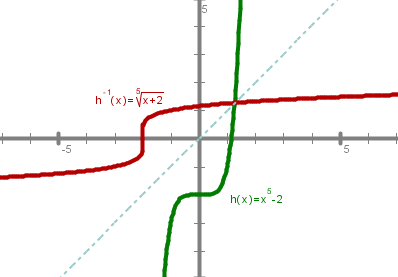
Graf lahko narišeš na dva načina:
- z vzporednim premikom korenske funkcije z eksponentom za vektor ,
- z izračunom inverzne funkcije, ki je v tem primeru potenčna funkcija , katere graf prezrcališ prek simetrale lihih kvadrantov.
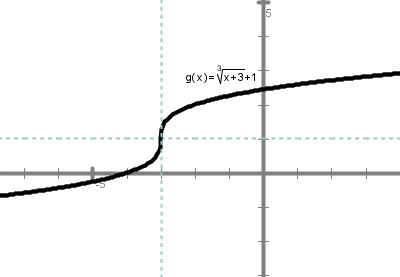
Graf funkcije .
Korenske funkcije s sodim korenskim eksponentom
Dano imaš funkcijo , . Nariši njen graf in se spomni njenih lastnosti.
| Graf funkcije |
Funkcija je soda, Funkcija je liha, Funkcija ni niti soda niti liha, (graf je zrcalen glede na ordinatno os), je padajoča je naraščajoča je konstantna na in je padajoča je naraščajoča je konstantna na in je omejena je navzgor omejena je navzdol omejena je neomejena , ni surjetivna injektivna , saj vzporednica abscisni osi seka graf dvakrat.
| Preveri |
1. Ali obstaja njena inverzna funkcija? Zakaj?
| Rešitev |
2. Kaj bi morali spremeniti, da bi funkcija postala bijektivna?
| Rešitev |
3. Poskusi zapisati predpis njene inverzne funkcije. V pomoč naj ti bo definicija korena sode stopnje. Kaj opaziš?
| Rešitev |
4. Nariši graf funkcije , in nariši še graf inverzne funkcije.
| Rešitev |
Pravilno
Bravo. Na vsa vprašanja si odgovoril pravilno.
Napačno
Nekateri tvoji odgovori so lahko pravilni, vendar ne vsi. Poskusi še enkrat.
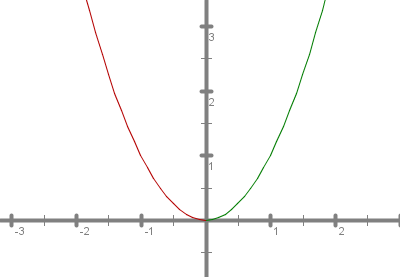
Ker funkcija ni injektivna, torej ni bijektivna, nima inverzne funkcije.
Ker funkcija kot realna funkcija ni niti injektivna niti surjektivna, bi morali odpraviti ti dve oviri. To najpreprosteje naredimo tako, da spremenimo (zožimo, skrčimo) definicijsko območje in zalogo vrednosti. Imamo dve možnosti:
ali . V obeh primerih je funkcija bijektivna, saj poljubna vzporednica seka sedaj graf v posameznem primeru natanko enkrat.
Če spet zamenjamo vlogi spremenljivk, dobimo:
Sedaj je treba upoštevati definicijo kvadratnega korena , , in dobimo:
Tako smo dobili predpis , ki ustreza drugi izbiri zožitve in , in sicer (glej prejšnjo rešitev).
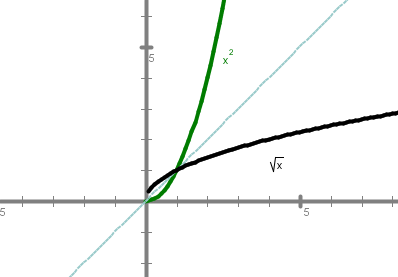
Grafi in lastnosti korenskih funkcij s sodim korenskim eksponentom
Grafi korenskih funkcij s sodim korenskim eksponentom
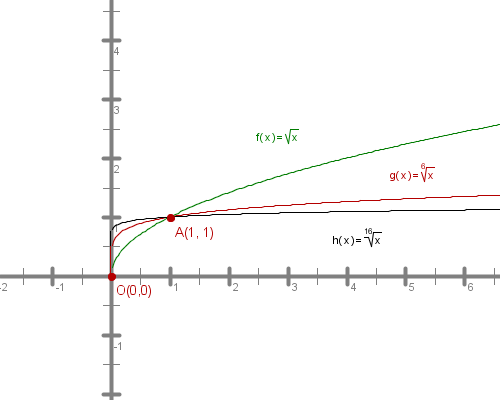
Na sliki so podani grafi korenskih funkcij z različnimi sodimi korenskimi eksponenti. Vidimo, da imajo podobno obliko in dve skupni točki. Strmina je odvisna od velikosti eksponenta; večji je eksponent, hitreje funkcija narašča na intervalu , na intervalu pa postanejo grafi funkcij z večjim korenskim eksponentom vse bolj položni.
Glavne lastnosti korenskih funkcij s sodim korenskim eksponentom:
- naraščajo na celotnem definicijskem območju,
- imajo dve skupni točki in ,
- omejene so navzdol in so pozitivne.
Naloga 2
Pazljivo preberi spodnje trditve in označi njihovo pravilnost oziroma nepravilnost.
1. Funkcija je definirana za .
Pravilno.
Napačno.
| Namig |
2. Graf funkcije dobimo z vzporednim premikom funkcije za vektor .
Pravilno.
Napačno.
| Namig |
3. Korenska funkcija je inverzna funkciji .
Pravilno.
Napačno.
| Namig |
| Preveri |
| Slika 1 |
| Slika 2 |
Pravilno
Bravo. Na vsa vprašanja si odgovoril pravilno.
Napačno
Nekateri tvoji odgovori so lahko pravilni, vendar ne vsi. Poskusi še enkrat.
Izraz pod korenom mora biti nenegativen, torej oziroma .
Gre za vzporedni premik za vektor .
Glej sliko 1 spodaj.
Glej sliko 1 spodaj.
Po zamenjavi spremenljivk in po ureditvi dobimo .
Glej sliko 2 spodaj.
Glej sliko 2 spodaj.
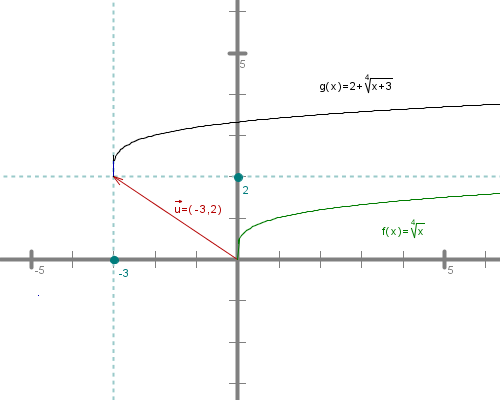
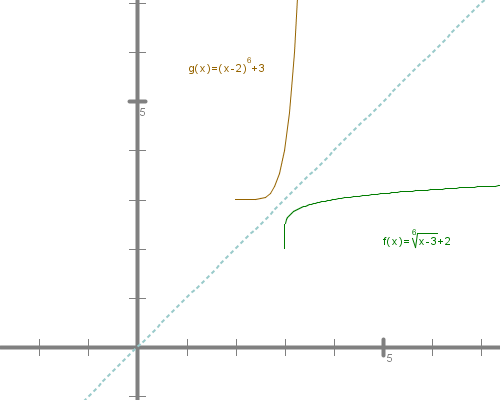
Graf funkcije , in graf funkcije , .
Naloga 3
Dano imaš potenčno funkcijo .
a) Zapiši njeno inverzno funkcijo .
b) Nariši grafe funkcij , , , .
c) Nariši graf funkcije in njene inverzne funkcije v isti koordinatni
sistem. Zapiši tudi predpis inverzne funkcije.
a)
Inverzna funkcija je:
b)
| Graf funkcij |
c)
Predpis inverzne funkcije je:
| Graf funkcij |
| Preveri |
Pravilno
Bravo. Na vsa vprašanja si odgovoril pravilno.
Napačno
Nekateri tvoji odgovori so lahko pravilni, vendar ne vsi. Poskusi še enkrat.
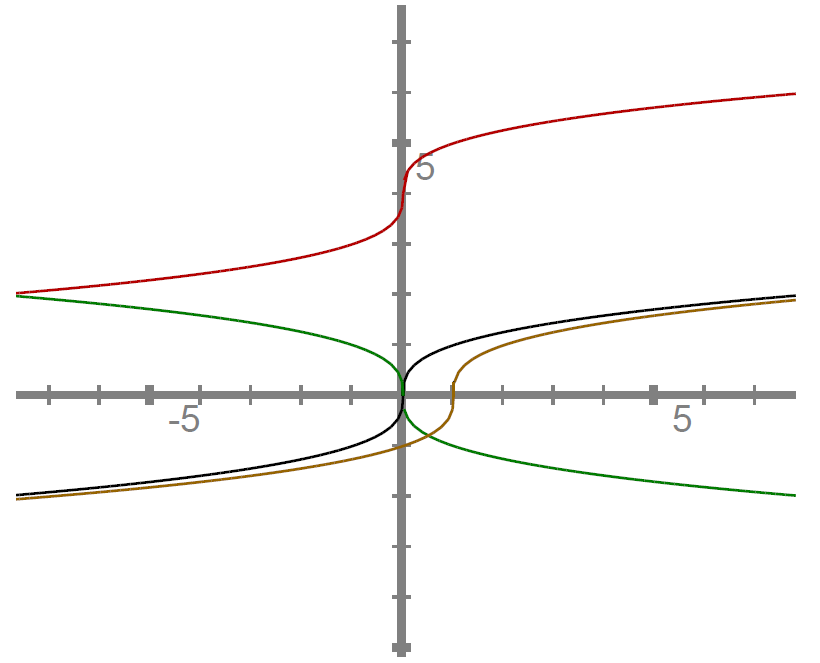
-črn,
-zelen,
-rjav,
-rdeč.
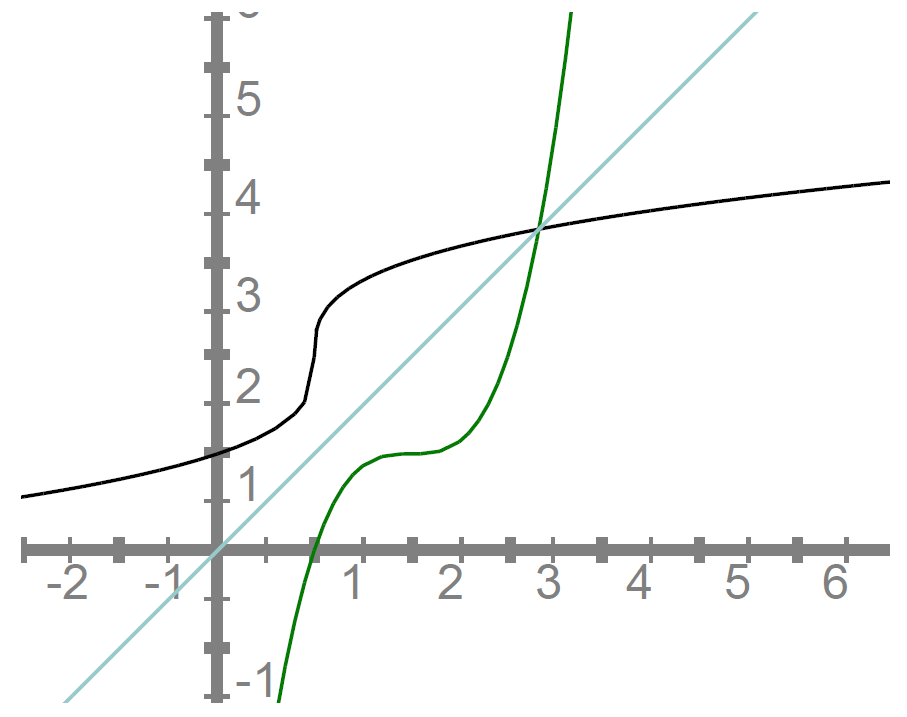
Naloga 4
Dano imaš korensko funkcijo .
a) Zapiši predpise funkcij , , in .
b) Zapiši predpise njihovih inverznih funkcij.
c) Nariši grafe korenskih funkcij primera a.
a) in b)
| Funkcija | Predpis funkcije | Inverzna funkcija |
|
| |
|
| |
|
| |
|
|
| Preveri |
c)
| Graf funkcij |
Pravilno
Bravo. Na vsa vprašanja si odgovoril pravilno.
Napačno
Nekateri tvoji odgovori so lahko pravilni, vendar ne vsi. Poskusi še enkrat.
- Ponovitev o korenih: Naloga 1
- Ponovitev o korenih: Naloga 2
- Povzetek ponovitve o korenih
- Korenske funkcije z lihim korenskim eksponentom
- Grafi in lastnosti korenskih funkcij z lihim korenskim eksponentom
- Naloga 1
- Korenske funkcije s sodim korenskim eksponentom
- Grafi in lastnosti korenskih funkcij s sodim korenskim eksponentom
- Naloga 2
- Naloga 3
- Naloga 4
