Z ukazom Hiperbola lahko v geogebri narišemo hiperbolo na tri načine:

1. Hiperbola[ <gorišče>, <gorišče>, <dolžina glavne osi> ] Klik

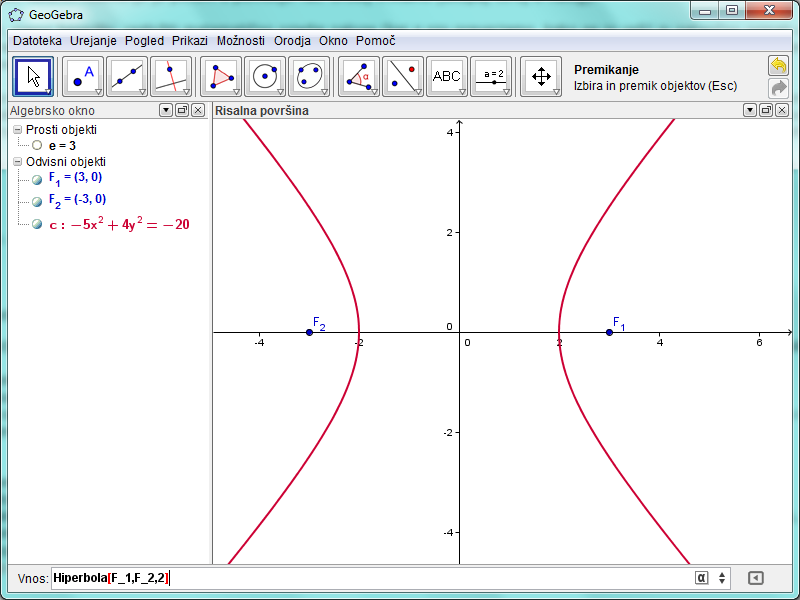
1. Hiperbola[ <gorišče>, <gorišče>, <dolžina glavne osi> ]
Pri prvi sintaksi ukaza sta prva dva parametra točki, ki sta gorišči hiperbole, tretji parameter pa je dolžina glavne (realne) osi.

Slika 1

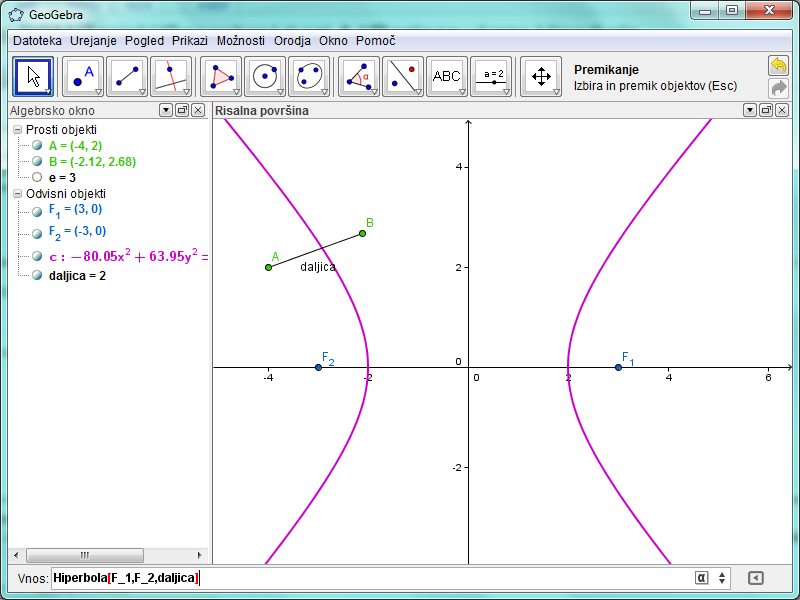
2. Hiperbola[ <gorišče>, <gorišče>, <daljica> ]
Pri drugi sintaksi za tretji parameter vnesemo daljico, katere dolžina se upošteva za dolžino glavne osi.

Slika 2

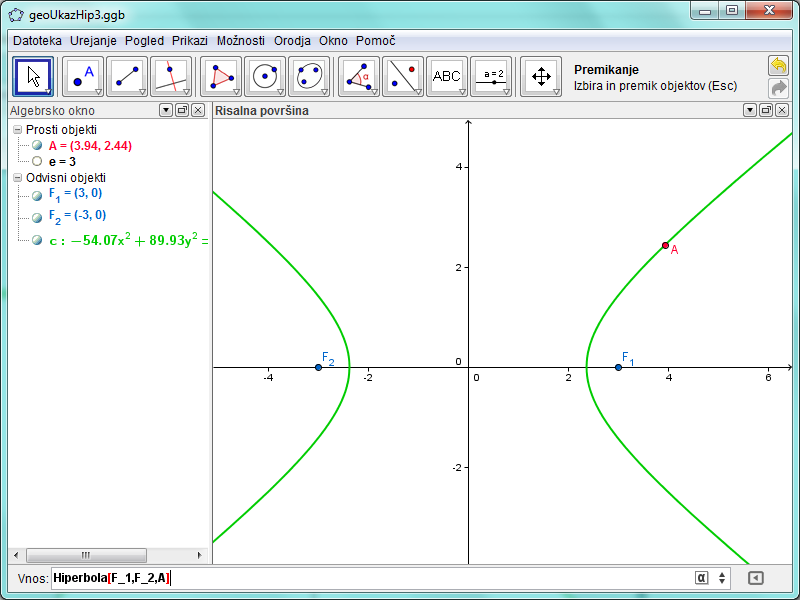
3. Hiperbola[ <točka>, <točka>, <točka> ]
Pri tretji sintaksi sta prva dva parametra prav tako goriščni točki, tretji parameter pa je točka na krivulji.

Slika 3

Hiperbola z realno(osnovno) polosjo in imaginarno polosjo ima po formuli za linearno ekscentričnost torej vrednost .

Hiperbola z enačbo ima torej gorišči v točkah in

Če torej povečamo vrednost realne polosi iz na , je potem .

Enačba ne velja več.

Elipsa nastane zaradi vrednosti , ki je večji od linearne ekscentričnosti, ki je za elipso