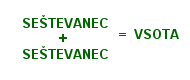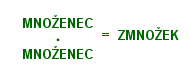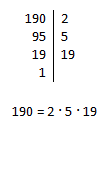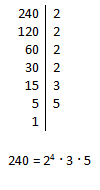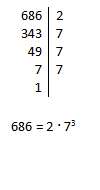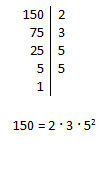Množico naravnih števil označimo z . To je množica števil od 1 do neskončno ali drugače .

Lastnosti naravnih števil:

• Naravnih števil je neskončno mnogo.
• Vsako naravno število ima svojega naslednika .
• Dve različni naravni števili imata različnega naslednika.

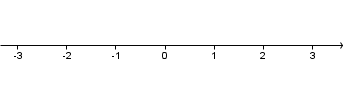
Upodobitev naravnih števil:

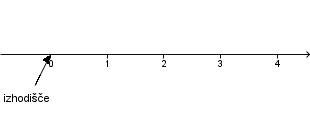
• Predstavimo jih na vodoravni premici, ki ji pravimo številska premica.
• Izberemo si izhodišče ali število 0 in za eno enoto v desno število 1.
• Enakomerno nanašamo še ostala števila in tako dobimo točke 2, 3, 4 ...

1. SEŠTEVANJE: Poljubni dve naravni števili in seštejemo in dobimo vsoto .

2. MNOŽENJE: Poljubni dve naravni števili in zmnožimo in dobimo produkt oziroma zmnožek , kjer imamo členov .

Radi bi kupili novo kolo, ki stane več, kot imate prihranjenega denarja. Da bi izračunali, koliko vam morajo starši posoditi, moramo uvesti novo množico števil.

To so cela števila, ki jih označimo z . Množico celih števil dobimo tako, da množici naravnih števil dodamo število 0 in negativna cela števila -1, -2, -3 ... Torej, to je množica števil od - neskončno pa do neskončno ali drugače . Številsko premico razširimo tako, da vsa naravna števila prezrcalimo čez izhodišče in število je nasprotno številu .

Večkratnik oziroma -kratnik števila je vsota enakih členov , kjer sta in celi števili. Primer: Večkratniki števila 4 so: -8, -4, 0, 4, 8, 12, 16 ...

Izraz je smiseln zapis, sestavljen iz števil, spremenljivk, operacij in oklepajev, ki določajo vrstni red računanja. Nekaj najbolj pomembnih izrazov:

Radi bi razcepili kvadratni tričlenik oblike oblike .

Včasih lahko tričlenik razcepimo kar na pamet, pri tem pa mora veljati:

kjer sta in celi števili.
Dobimo . Tej formuli rečemo Vietovo pravilo.

Zgleda

Za rojstni dan smo dobili 14 bonbonov, ki jih želimo razdeliti med prijatelje:

• 14 prijateljev lahko obdarimo z 1 bonbonom.
• 7 prijateljev lahko obdarimo z 2 bonbonoma.
• 2 prijatelja lahko obdarimo s 7 bonboni.
• 1 prijatelja lahko obdarimo s 14 bonboni.

Dobili smo tudi 7 čokolad, ki jih želimo pravično razdeliti. Tu imamo le dve možnosti: da en prijatelj dobi vseh 7 čokolad ali da 7 prijateljev dobi po 1 čokolado.

Lahko bi rekli tudi drugače: število 7 ima le dva delitelja, to sta 1 in 7, število 14 pa več, to so 1, 2, 7 in 14.

• Naravno število deli število , če lahko zapišemo v obliki . natako tedaj, ko velja .
• Naravno število je sodo takrat, ko se ga da zapisati v obliki , kjer je naravno število.
• Naravno število je liho takrat, ko se ga da zapisati v obliki ali , kjer je naravno število.

Oglejmo si število 2476. To število je sestavljeno iz enic, desetic, stotic in tisočic. Lahko zapišemo tudi kot 6E 7D 4S 2T. To pa so ravno potence števila 10. Lahko pa to število zapišemo tudi drugače:

Naj bo neko naravno število. Desetiški zapis tega števila je

kjer so števke od 0 do 9.

Zapišimo število 2476 v desetiškem zapisu: .

S katerimi števili od 2 do 10 je deljivo število 254782222445425423? Ker bi bilo preverjanje tega s kalkulatorjem ali pisnim deljenjem na pamet prezamudno, lahko to storimo s pomočjo kriterijev za deljivost:

Glede na število deliteljev lahko števila razdelimo v skupine:

1. Število 1, ki ima samo enega delitelja, samega sebe.
2. Števila, ki imajo natanko dva delitelja, samega sebe in število 1. To so praštevila.
3. Števila, ki imajo več kot dva delitelja. To so sestavljena števila.

Osnovni izrek:
Vsako naravno število lahko zapišemo na natanko en način, in sicer kot produkt samih praštevil, pri čemer lahko posamezno praštevilo nastopi večkrat.

Naj bosta in naravni števili in . Potem obstajata natanko določeni nenegativni celi števili in , tako da velja:

.

... deljenec
... delitelj
... količnik ali kvocient
... ostanek

Primeri:

Imamo števili 20 in 24.

• Delitelji števila 20: .
• Delitelji števila 24: .
• Skupni delitelji: .
• Največji skupni delitelj: 4.

Največji skupni delitelj dveh števil in je tako največje naravno število, ki hkrati deli in .

Postopek:

• Dana števila razcepimo na prafaktorje.
• Največji skupni delitelj dveh ali več števil je produkt prafaktorjev, ki so skupni vsem razcepom.
• Pri posameznem prafaktorju vzamemo najmanjšega od eksponentov.

Če za dve naravni števili velja, da je njun največji skupni delitelj enak 1, potem pravimo, da sta si števili tuji.

Poiščimo največji skupni delitelj števil 120, 144 in 180.
Rešitev

• Razcepimo števila na prafaktorje:

Za največji skupni delitelj vzamemo tista praštevila, ki so skupna vsem trem razcepom, in pri posameznih številih najmanjšega od eksponentov. Skupni sta števili 2 in 5 z eksponentoma 1.