Vir:
Poskusni kolokvij iz Linearne algebre, 14.1.2005, 1. naloga, dosegljiva v dokumentu.
Besedilo naloge:
Reši sistem enačb
1.naloga
Poskusni kolokvij iz Linearne algebre, 14.1.2005, 1. naloga, dosegljiva v dokumentu.
Reši sistem enačb
1.naloga
Glej Reševanje sistema linearnih enačb.
Sistem linearnih enačb zapišemo v matrični obliki A*x=b (A je matrika sistema, vektor b je desna stran, x pa vektor neznank) in ga rešimo z Gaussovo metodo. Najprej izračunamo rang matrike A, tvorjene iz koeficientov pri neznankah. Nato razširjeni matriki sistema (oznaka naj bo Ab) s pomočjo elementarnih transformacij poiščemo vrstično kanonično formo. Število pivotov v vrstični kanonični formi je enako rangu razširjene matrike sistema Ab, ki je enako rangu matrike A, če naj bo sistem rešljiv. Sistem ima natanko eno rešitev, če je rang enak številu neznank oz. ima več (neskončno) rešitev, če je rang manjši od števila neznank (ta razlika pove število parametrov).
1.naloga
Za reševanje linearnih sistemov imamo v Matlabu vgrajeno funkcijo linsolve ali operator \. Če zastavljeno nalogo želimo rešiti v Matlabu, le-ta vrne opozorilo, da je matrika singularna (detA=0) in ne izračuna vseh rešitev, ker jih je neskončno. Z Matlabom sem izračunala rang matrike A in rang razširjene matrike Ab. V obeh primerih dobim enak rezultat, to je 3, kar pomeni, da je sistem rešljiv, in sicer ima neskončno rešitev, saj je število neznank 4, kar je več kot rang, torej imamo en parameter. Z Matlabom sem poiskala vrstično kanonično formo razširjene matrike Ab (Drugi vrstici sem odštela dvakratnik prve vrstice , tretji vrstici sem prištela prvo, četrti pa odštela prvo. Nato sem tretji vrstici prištela trikratnik četrte vrstice in dvakratnik druge.) in iz nje prebrala rešitev: je parameter,, in .
Če nalogo rešujemo z Mathematico, je ta program sicer vrnil rešitev, a ta je bila le ena izmed mnogih.
2.naloga
Poskusni kolokvij iz Linearne algebre, 14.1.2005, 2. naloga, dosegljiva v dokumentu.
Reši enačbo
Glej Determinanta matrike.
2.naloga
Nalogo sem rešila s pomočjo Mathematice, kjer sem z ukazom Det[matrika] prvo izračunala determinanto matrike. Nato sem rezultat izenačila z -1 in izračunala, koliko je x. Rešitev: .

3.naloga
Poskusni kolokvij iz Linearne algebre, 6.1.2006, 1. naloga, dosegljiva v dokumentu.
Poišči pogoj za parametre a, b, c, pri katerem je rešljiv sistem linearnih enačb:
Poišči vse rešitve, kadar obstajajo.
3.naloga
Glej Reševanje sistema linearnih enačb.
Sistem linearnih enačb bo rešljiv natanko tedaj, ko bo rang matrike A enak rangu razširjene matrike. Zato najprej izračunam rang matrike A. Nato s pomočjo elementarnih transformacij razširjeno matriko sistema privedem do ustrezne oblike (vrstična kanonična forma). Ker je desna stran sistema napisana s parametri, v Matlabu izračunamo le transformacije na matriki A, desno stran pa izračunam na roko (vrstni red transformacij je pomemben, zato si jih zapisujemo).
3.naloga
S pomočjo Matlaba izračunam vrstično kanonično formo matrike A in si zapomnim vrstni red elementarnih transformacij, ker jih moram potem uporabiti tudi na desni strani : drugi vrstici odštejem prvo
, tretji vrstici prištejem dvakratnik prve , nato pa še tretji vrstici prištejem trikratnik druge vrstice
.
Vse to ročno izračunamo za desno stran in vidimo, da bo sistem rešljiv le pod pogojem, če bo –a+3b+c=0, ker bo le takrat rang razširjene matrike enak rangu matrike A. Ker je število neznank 3, rang pa 2, pomeni, da imamo en parameter in to je z. Izrazimo y in nato še x. Rešitev: Sistem je rešljiv, ko , je parameter, in .
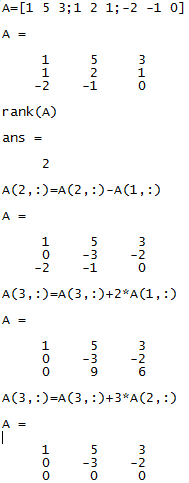
4.naloga
2. kolokvij iz Linearne algebre, 10.12.1998, 3. naloga, dosegljiva v dokumentu.
Poišči vsa taka realna števila x, za katera je determinanta enaka 0.
4.naloga
4.naloga
Nalogo rešimo tudi s pomočjo Mathematice, kjer z ukazom Det[matrika] prvo izračunamo determinanto matrike. Nato rezultat enačimo z 0 in z ukazom Solve[%==0,Reals] izračunamo, koliko je x. Rešitev: , ,
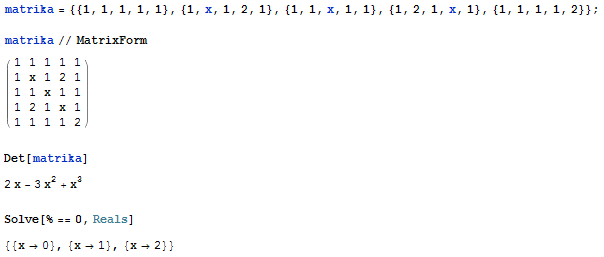
5.naloga
3. kolokvij iz Linearne algebre, 3.4.2008, 2. naloga, dosegljiva v dokumentu.
Poišči vsa števila x ϵ R, za katera velja
Glej Determinanta matrike.
5.naloga
Nalogo rešimo s pomočjo Mathematice, kjer z ukazom Det[matrika] prvo izračunamo determinanto matrike. Nato rezultat enačimo z in z ukazom Solve[%==0,Reals] izračunamo, koliko je x. Rešitev: , , , , .

6.naloga
Splošna matura, 4.6.2011 (Višja raven, Izpitna pola 2) – 2. naloga, dosegljiva v dokumentu.
Dano je zaporedje s splošnim členom
6.naloga
Glej Limita zaporedja.
Ročno računanje:
Število 1,97 ni člen danega zaporedja. Dokaz:
Limita:
6.naloga
Členi, ki niso v ε-okolici števila 2, če je :
Členi od do niso v ε –okolici.
6.naloga
Pri tej nalogi si pomagamo z Mathematico. Preverimo, če so rezultati pravilni. Z ukazom Solve[enačba] rešimo dano enačbo, z ukazom Limit[zaporedje] pa izračunamo limito danega zaporedja. N[%] mi zadnji rezultat pretvori v število.

7.naloga
4. poskusni kolokvij iz Linearne algebre, 25.4.2005, 4. naloga, dosegljiva v dokumentu.
Nariši krivuljo .
7.naloga
Glej Kvadratne forme.
Kvadratni formi pripada matrika . Ta ima karakteristični polinom . Lastni vrednosti sta in . Glavni osi sta in , oziroma premici z enačbama in . V novem koordinatnem sistemu ima krivulja enačbo , oziroma . Krivulja je elipsa in njeni polosi sta in .
7.naloga
Nalogo rešimo v Geogebri in v Mathematici. V Mathematici z ukazom ContourPlot[enačba, {x, xmin, xmax}, {y,ymin,ymax}] narišemo graf implicitno podane krivulje na območju od xmin do xmax na x osi ter od ymin do ymax na y osi. V Geogebri pa enačbo krivulje preprosto vnesemo v vnosno vrstico.
8.naloga
3. kolokvij iz Linearne algebre, 11.3.2004, 4. naloga, dosegljiva v dokumentu.
Izračunaj lastne vrednosti in lastne vektorje matrike .
8.naloga
Glej Lastne vrednosti in lastni vektorji.
Kompleksno število imenujemo lastna vrednost za , če obstaja tak neničeln vektor , da je . Vektor imenujemo lastni vektor za pri lastni vrednosti . . Polinom v spremenljivki imenujemo karakteristični polinom matrike . Kompleksno število je torej lastna vrednost matrike natanko tedaj, ko je ničla karakterističnega polinoma .
8.naloga
Nalogo rešimo s programom Mathematica. Najprej vnesemo matriko c. Nato z ukazom Eigenvalues[c] izračunamo lastne vrednosti matrike c. Z ukazom Eigensystem[c] pa izračunamo še pripadajoče lastne vektorje. Rešitev: , , , , , .

9.naloga
3. poskusni kolokvij iz Linearne algebre, 9.3.2004, 4. naloga, dosegljiva v dokumentu.
Izračunaj lastne vrednosti in lastne vektorje matrike .
9.naloga
Glej Lastne vrednosti in lastni vektorji.
Karakteristični polinom za je in . Lastni vektor , ki pripada lastni vrednosti zadošča zvezi . Izberemo . Podobno za lastni vektor , ki pripada lastni vrednosti in zadošča zvezi , izberemo .
9.naloga
Nalogo rešimo s programom Mathematica. Vnesemo matriko c in nato z ukazom Eigensystem[c] v enem koraku izračunamo lastne vrednosti matrike c ter pripadajoče lastne vektorje. Rešitev:
, ,, .

10.naloga
4. kolokvij iz Matematike 1, 6.6.2011, 2. naloga, dosegljiva v dokumentu
10.naloga
Glej Integral.
Nedoločeni integral dane funkcije f je funkcija F, katere odvod je enak dani funkciji f. V tem smislu je integriranje obratna operacija kot odvajanje. Rezultat nedoločenega integrala imenujemo primitivna funkcija. Določeni integral pa je povezan s ploščino lika, omejenega z grafom funkcije f. Naj bosta dana pozitivna funkcija f realne spremenljivke x in interval [a, b] na številski premici. Določeni integral funkcije f je ploščina lika, ki ga omejujejo graf funkcije f, os x ter navpični premici x = a in x = b. Določeni in nedoločeni integral povezuje osnovni izrek infinitezimalnega računa, ki se imenuje tudi Newton-Leibnizeva formula: Ploščino omejenega lika izračunamo tako, da najprej z nedoločenim integralom izračunamo primitivno funkcijo F, potem pa vanjo vstavimo meji intervala: p = F(b) − F(a).
Ročno računanje:
Opomba:
10.naloga
Nalogo rešimo z Mathematico in z Matlabom. Seveda oba programa vrneta enake rešitve, le v malo drugačni obliki. V Mathematici integral izračunamo z ukazom Integrate, v Matlabu pa z ukazom int.
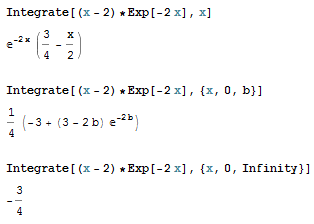

11.naloga
1. izpit iz Matematike 1, 20.6.2011, 2. naloga, dosegljiva v dokumentu.
Podano je rekurzivno zaporedje , . Dokaži, da je zaporedje naraščajoče, konvergentno in izračunaj njegovo limito.
11.naloga
Glej Zaporedja.
Najprej izračunajmo nekaj členov zaporedja: , , Videti je, da je zaporedje naraščajoče.
Dokaz:
Zaporedje je naraščajoče, če je in . za vsak n iz množice naravnih števil. Trditev dokažemo s popolno indukcijo. Za trditev velja.
Ker po predpostavki popolne indukcije velja, da je in linearna funkcija.
in
za poljubne iz množice naravnih števil. Zaporedeje je naraščajoče. Zaporedje je navzgor omejeno s . Torej, ker je zaporedje naraščajoče in omejeno, je konvergentno. Konvergira k zgornji meji.
11.naloga
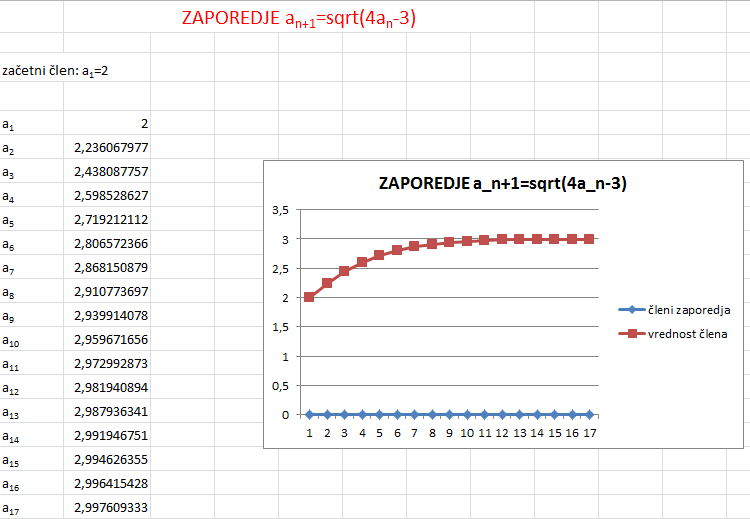
Z Excelom izračunamo nekaj členov zaporedja. Členi zelo hitro konvergirajo k limiti. Narišemo tudi graf.
12.naloga
3. izpit iz Matematike 1, 30.8.2011, 2. naloga, dosegljiva v dokumentu.
Določi definicijsko območje, ničle, ekstreme, intervale naraščanja in padanja, območje konveksnosti in konkavnosti, razišči obnašanje na robu definicijskega območja ter nato čim bolj natančno nariši graf funkcije .
12.naloga
Definicijsko območje naše funkcije je . Graf funkcije seka os (ničla) v točki : , os (začetna vrednost) pa v : . Ekstreme dobimo, ko izračunamo , in s tem tudi intervale naraščanja in padanja: minimum , funkcija pada na intervalu in narašča na . Območje konveksnosti pa dobimo, ko izračunamo . Funkcija bo konveksna na intervalu in konkavna na . Asimptota funkcije je . Ko pošljemo proti neskončno se graf funkcije približuje asimptoti, a se je nikoli ne dotakne.
12.naloga
Graf dane funkcije narišemo v Geogebri, tako da v vnosno vrstico vnesemo enačbo funkcije. Za izračun ničle in ekstrema si pomagamo z Matlabom. Najprej definiramo funkcijo y. Nato s funkcijo solve(y,0) izračunamo ničlo funkcije. Z ukazom diff(y) izračunamo odvod funkcije. Ekstrem poiščemo tako, da zopet uporabimo funkcijo solve.
13.naloga
Splošna matura, 4.6.2011 (Osnovna raven, Izpitna pola 1) – 2. naloga, dosegljiva v dokumentu.
Prvi člen aritmetičnega zaporedja je -4, peti člen pa 8. Izračunajte diferenco (razliko) in stoti člen tega zaporedja.
13.naloga
Glej Aritmetično zaporedje.
Splošni člen aritmetičnega zaporedja je . V enačbo vstavimo podatke in izrazimo diferenco: .
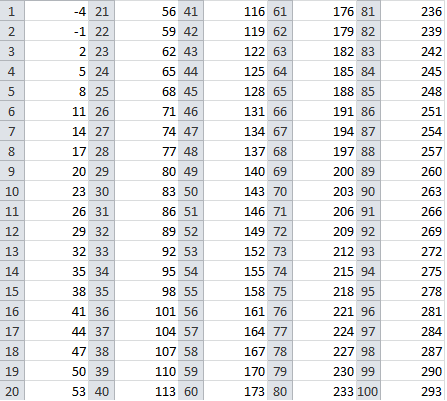
Sedaj lahko izračunamo tudi stoti člen: .
13.naloga
V Excel sem vnesla prvi in drugi člen zaporedja, ju označila in potegnila vse do stotega člena. Tako sem preverila, če dobim enako rešitev.
14.naloga
Splošna matura, 4.6.2011 (Osnovna raven, Izpitna pola 1) – 3. naloga, dosegljiva v dokumentu.
Poenostavite izraz .
14.naloga
Glej Potence.
Upoštevamo pravila za računanje s potencami (potenciranje, množenje, deljenje).
14.naloga
V Mathematico vtipkamo dani izraz, pritisnemo Shift+Enter in dobim poenostavljen izraz.
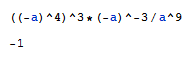
15.naloga
Splošna matura, 4.6.2011 (Osnovna raven, Izpitna pola 1) – 5. naloga, dosegljiva v dokumentu.
Kompleksno število zapišite v obliki , , .
15.naloga
Glej Kompleksna števila.
Kompleksna števila definiramo kot . Število imenujemo realna komponenta (Re ), število pa imaginarna komponenta (Im ) kompleksnega števila ; število je imaginarna enota.
Računanje na roko:
15.naloga
V Mathematici z ukazom Simplify[izraz] poenostavimo dani izraz. Imaginarno enoto pišemo z veliko črko . Rešitev: .
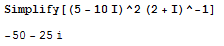
16.naloga
Splošna matura, 4.6.2011 (Osnovna raven, Izpitna pola 1) – 6. naloga, dosegljiva v dokumentu.
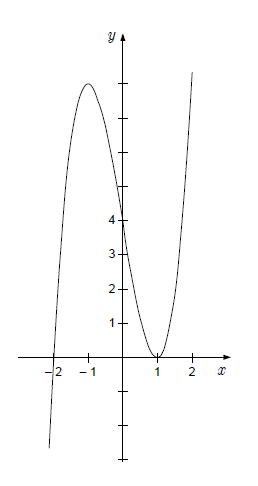
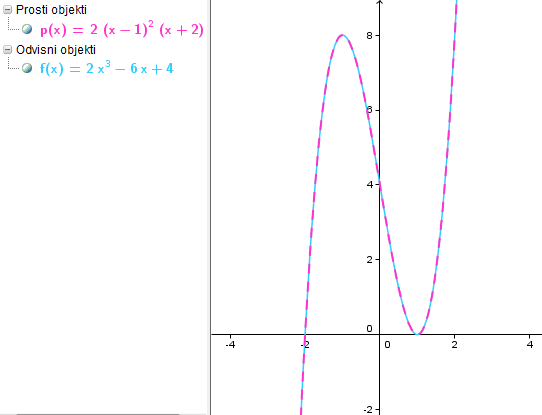
Zapišite polinom tretje stopnje, katerega graf je narisan v koordinatnem sistemu.
16.naloga
Glej Polinomi.
Iz slike vidimo, da ima polinom ničlo v in dvojno ničlo v ter začetno vrednost .
Vse to vstavimo v enačbo in dobimo ;
16.naloga
V Geogebro vnesemo enačbo polinoma in preverimo, če dobimo enak graf.
17.naloga
Splošna matura, 4.6.2011 (Osnovna raven, Izpitna pola 1) – 11. naloga, dosegljiva v dokumentu.
Marjetica ima 21 prijateljic in 11 prijateljev (le enemu prijatelju je ime Andrej in le enemu Borut). Na zabavo bo povabila 3 svoje prijateljice in 4 prijatelje. Na koliko načinov lahko to stori? Kolikšna je verjetnost, da bosta med temi povabljenci Andrej in Borut, če bo Marjetica izbirala povabljence naključno?
17.naloga
Glej Kombinacije.
Marjetica bo izmed 21 prijateljic izbrala 3 prijateljice: načinov, in izmed 11 prijateljev bo izbrala 4 prijatelje: načinov. Verjetnost, da bosta med povabljenci Andrej in Borut pa je: .
Število ugodnih izidov je , saj je že izbrala Andreja in Boruta (to pomeni, da izbira le še 2 prijatelja izmed 9).
Število vseh izidov pa je .
In verjetnost je
17.naloga
Za reševanje naloge potrebujemo znanje kombinatorike in verjetnostnega računa. S programom si lahko pomagamo le izračunati sestavljen račun.
V Mathematici binomski simbol izračunamo z ukazom Binomial[n,k], v Matlabu pa z ukazom nchoosek(n,k).

