Premiki in raztegi

Avtor: Karmen Perko

Učni cilji: - Iz zapisa prepozna premik/razteg. - Zna preoblikovati zapis glede na premik/razteg grafa. - Zna narisati graf, če je podan predpis funkcije.

Premiki in raztegi

Kako premakrniti omaro?

Nekje v prostoru imamo postavljeno omaro. Želeli bi jo premakniti. Ker je težka, nam mora nekdo pomagati. Kaj vse se moramo dogovoriti z našim pomočnikom?

Nepremaknjena omara

Kam jo bova premaknila? Npr. v levi kot.
V kateri smeri jo bova nesla? Npr. po diagonali.

Oba zgornja podatka bi lahko družili tudi v podatek, ki opisuje premik v posamezno smer glede na trenutno postavitev omare. Premikamo se lahko levo in desno ter naprej in nazaj. Tako bi naprimer rekli, da bomo šli tri korake naprej in šest korakov v levo.

Možni premiki

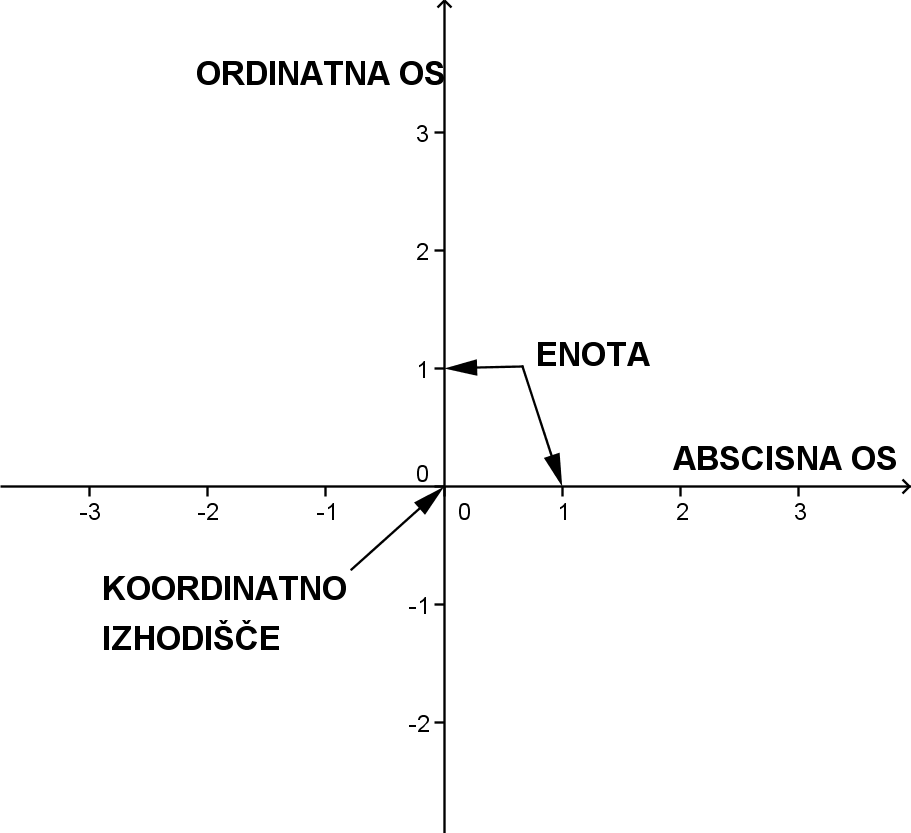
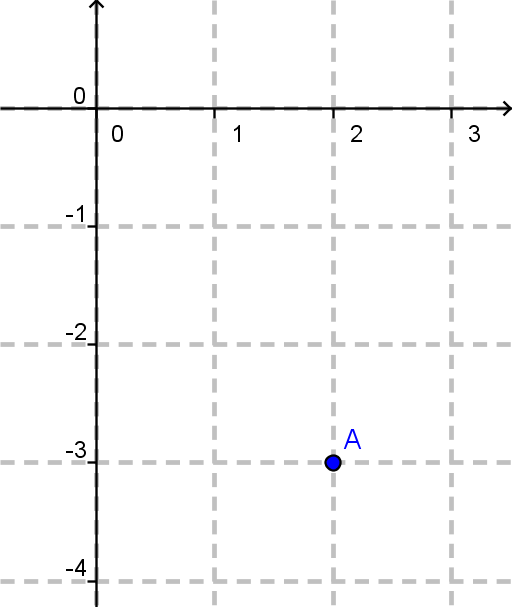
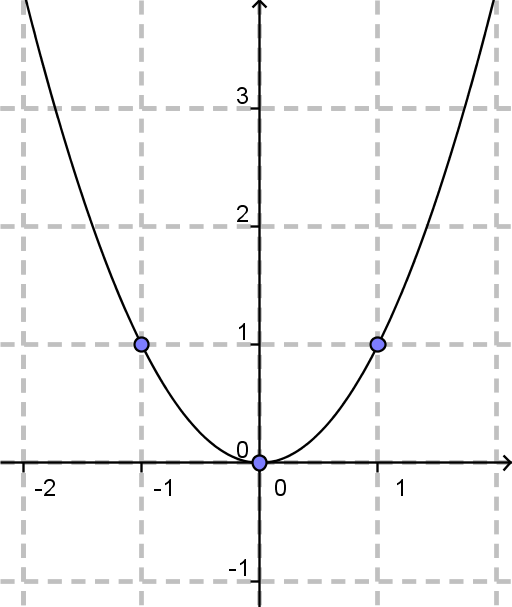
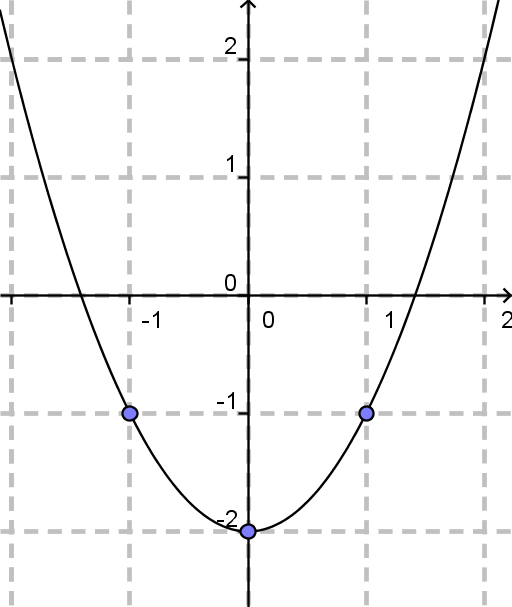
Tako premikanje nas spomni na koordinatni sistem.

Koordinatni sistem v ravnini

Spomnimo se koordinatnega sistema v ravnini. Določen je z dvema pravokotnima premicama. Njuno presečišče imenujemo koordinatno izhodišče. Premici predstavljata abscisno (x) in ordinatno (y) os. Na vsaki osi je določena enota, s pomočjo katere lahko sporočamo, za koliko je neka točka oddaljena od koordinatnega izhodišča. Enota predstavlja število 1.

Koordinatni sistem

Če hočemo povedati, kje v koordinatnem sistemu se nahaja poljubna točka, moramo povedati njenen koordinate. To je, da povemo odmik točke od koordinatnega izhodišča v smeri x-osi in v smeri y-osi.

Primer:

Točka A(2, -3)

Točka A ima koordinate (2, -3). To pomeni, da je od koordinatenga izhodišča odmaknjena za 2 enoti v desno in za 3 enote dol.

Položaja točke v koordinatnem sistemu ni težko določiti. Kako pa bi opisali položaj graf neke funkcije v koordinatnem sistemu?

Premiki grafov poljubnih funkcij

Premike grafov si bomo pogledali kar na primeru kvadratne funkcije. Opazovali bomo funkcijo s predpisom f(x) = x^2.

Graf nepremaknjene kvadratne funkcije

Kako bi opisali, da smo graf kvadratne funkcije premaknili za dve enoti navzdol?

Sporočimo lego najnižje točke funkcije - temena.
- Teme je v točki (0,-2). Vse točke, ki jih graf vsebuje, se premaknejo za dve enoti navzdol.
Funkcijo narišemo.
- Premik za dve enoti navzdol
Sporočimo predpis premaknjene funkcije.
- Kakšen je predpis premaknjene funkcije?

Premik vzdolž y-osi

Ker vemo, da premik navzdol spremeni samo y-koordinato točke, to pomeni, da se mora tudi v predpisu spremiti vrednost . Torej bomo za premik za 2 enoti navzdol od osnovnega predpisa odšteli 2.

Viri in literatura