Preberi tri besede in jih izpiši tako, kot bi se lahko sekale v križanki. Program naj poišče vsaj eno rešitev.

Besedilo problema
Preberi tri besede in jih izpiši tako, kot bi se lahko sekale v križanki. Program naj poišče vsaj eno rešitev.

Ideja reševanja problema
Reševanje problema (iskanje rešitve)
Rešitev bomo shranili v tabelo, dolžine 5 elementov. Prvi in drugi element povesta, pri kateri črki (indeks ležeče besede) prva in druga pokončna beseda sekata ležečo. Tretji in četrti element povesta, kje (indeksa pokončnih besed) ležeča beseda seka prvo in drugo pokončno. Peti element pa pove, katera beseda je nastavljena za ležečo. Na začetku, ko še nimamo nobene rešitve, ima tabela naslednje vrednosti: .
Rešitev lahko poiščemo v treh primerih - vsakič za ležečo besedo nastavimo drugo besedo (zamenjamo vrstni red besed, da je ležeča beseda vedno na prvem mestu). Z iskanjem rešitve končamo takoj, ko najdemo prvo ustrezno rešitev. Če v nobenem od teh primerov ne najdemo rešitve, ta ne obstaja.
Ko iščemo rešitev v posameznem primeru, potujemo po črkah ležeče besede. Če se trenutna črka ne nahaja v nobeni izmed pokončnih besed, nadaljujemo z naslednjo črko.
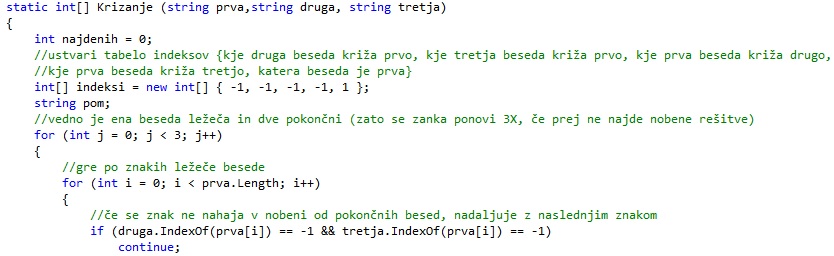
Reševanje problema (iskanje rešitve)
Če se trenutna črka nahaja v obeh pokončnih besedah, najprej preverimo, če že imamo shranjeno rešitev, ko pokončni besedi sekata ležečo pri isti črki. V tem primeru zamenjamo rešitev samo pri drugi pokončni besedi oz. besedi, ki je shranjena na tretjem mestu.
Če pa za prvo pokončno besedo še nismo našli rešitve, ji dodelimo trenutno. Prav tako velja za drugo pokončno besedo. V tem primeru tudi povečamo število najdenih rešitev. Na koncu želimo imeti dve najdeni rešitvi - eno za prvo in drugo za drugo pokončno besedo.
Da si zapomnemo trenutno rešitev za prvo pokončno besedo, moramo spremeniti prvi element v tabeli (pri kateri črki se trenutno nahajamo) in tretji element v tabeli (na katerem mestu se nahaja trenutna črka v pokončni besedi). Za drugo pokončno besedo naredimo isto, le da spreminjamo drugi in četrti element v tabeli.
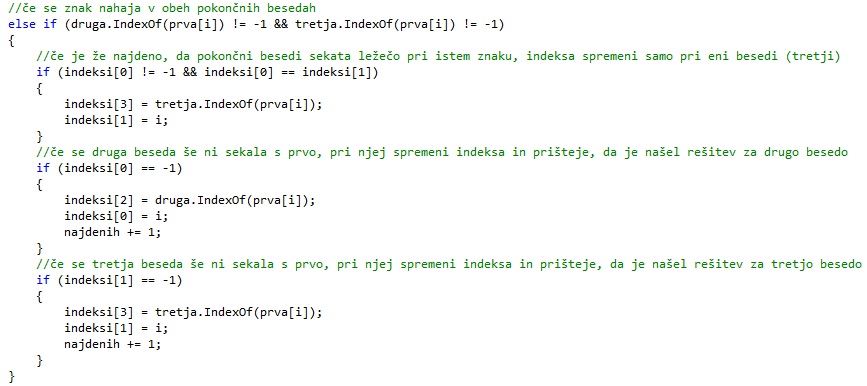
Reševanje problema (iskanje rešitve)
Če se črka ne nahaja v obeh pokončnih besedah, ampak samo v prvi pokončni, preverimo, če za prvo pokončno besedo še ni rešitve. V tem primeru shranimo trenutno rešitev. Trenutno rešitev shranimo tudi v primeru, če rešitev za prvo pokončno besedo že obstaja, a ima druga pokončna beseda rešitev pri isti črki.
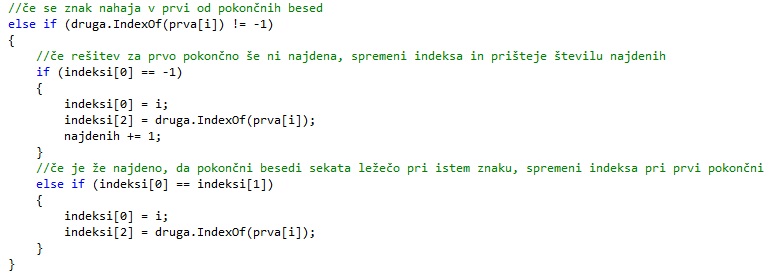
Enako naredimo za drugo pokončno besedo, če se trenutna črka nahaja samo v njej in ne tudi v prvi pokončni.
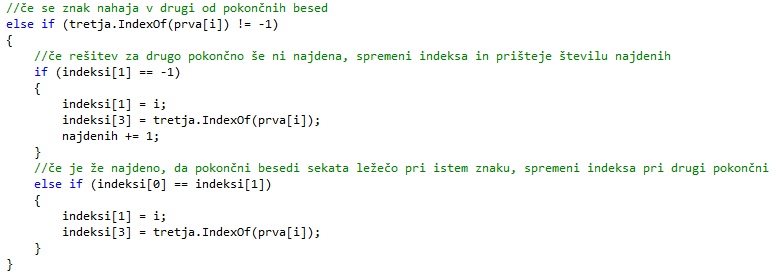
Reševanje problema (iskanje rešitve)
Ko preverimo, če se v kateri pokončni besedi nahaja trenutna črka in izvedemo, kar je potrebno, preverimo še, če smo že našli dve rešitvi, ki se ne nahajata pri isti črki. V tem primeru končamo in vrnemo dobljeno rešitev. Drugače pa ponastavimo vrednosti v tabeli in zamenjamo vrstni red besed ter vse po enakem postopku izvedemo še enkrat.
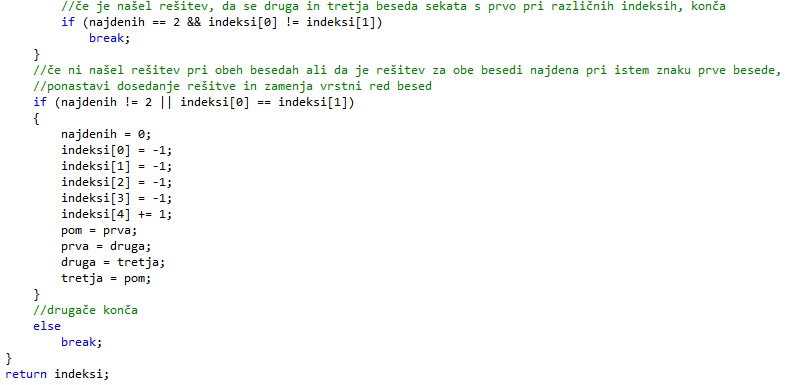
Reševanje problema (izpis rešitve)
Ko želimo zapisati rešitev križanja besed, potrebujemo indekse, kjer se besede križajo med seboj in katera beseda je ležeča. Ko imamo te podatke pa preverimo, če moramo slučajno zamenjati vrstni red besed. V tem primeru jih krožno zamenjamo. Če pa ima zadnji element v tabeli rešitev vrednost 4, to pomeni, da rešitve ni in vrnemo rešitev, da se besede na sekajo.
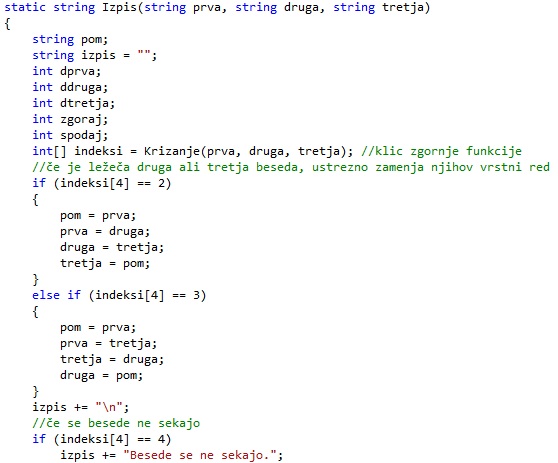
Reševanje problema (izpis rešitve)
Če dobimo rešitev, da se besede sekajo, si zapomnemo dolžine besed. Za lažje zapisovanje rešitve pa moramo preveriti tudi, koliko vrstic je nad ležečo besedo in koliko ostalih. Za ugotavljanje, koliko je vrstic zgoraj, uporabimo indeksa, ki povesta, kje ležeča beseda seka pokončni. Se pravi: večji indeks pove število vrstic nad ležečo besedo. Za ostale vrstice pa indeksa križanja pokončnih besed odštejemo od dolžine iste besede in si zapomnemo večjo vrednost.
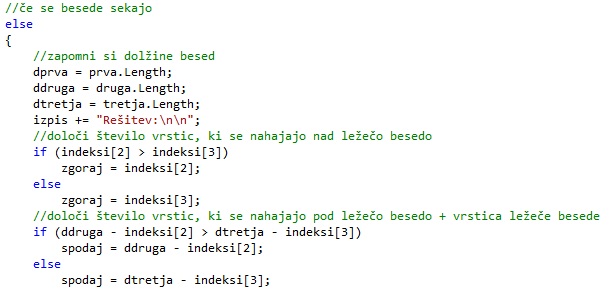
Reševanje problema (izpis rešitve)
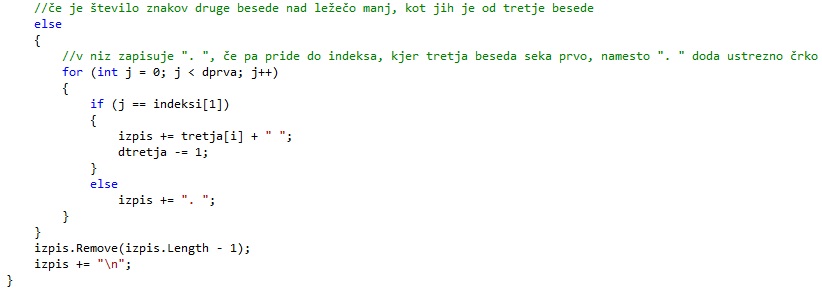
Sedaj lahko nadaljujemo z zapisom rešitve. Najprej zapišemo toliko vrstic, kolikor je absoluta razlika med številoma črk prve in druge pokončne besede, ki ležijo nad ležečo.
Za vsako vrstico v primeru, če ima prva pokončna beseda več črk nad ležečo, kot druga, potujemo po indeksih ležeče besede. Če pridemo do indeksa, kjer prva pokončna beseda seka ležečo, v zapis dodamo ustrezno črko pokončne besede, drugače pa dodamo piko. Vsakič, ko zapišemo črko, zmanjšamo dolžino te besede za ena, kar nam bo pomagalo pri nadaljnjem zapisovanju rešitve.
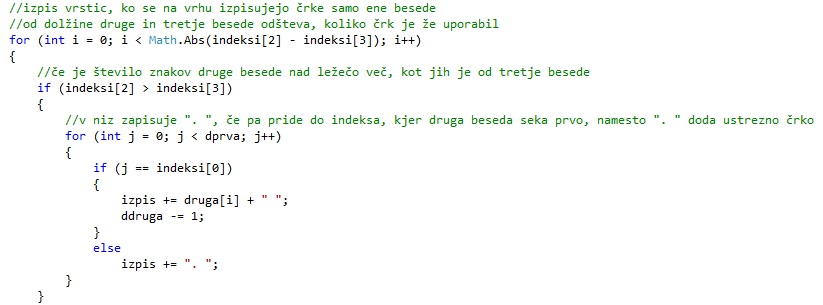
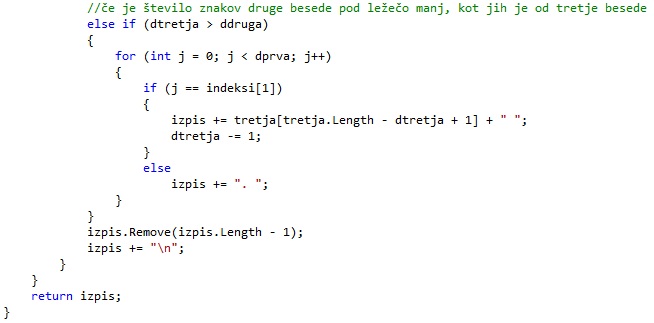
Če pa ima druga pokončna beseda več črk nad ležečo, kot prva, je postopek isti, le da smo pozorni na indeks, kjer ta beseda seka ležečo.
Reševanje problema (izpis rešitve)
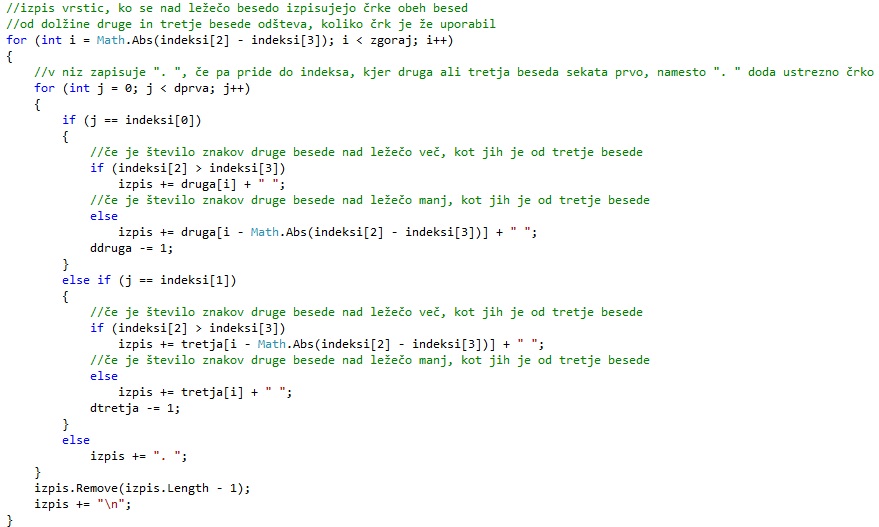
Nadaljujemo z zapisom rešitve do ležeče besede, kjer v vrsticah zapisujemo črke obeh pokončnih besed. Teh vrstic je: od števila vseh zgornjih odštejemo število vrstic, ki smo jih že zapisali.
Zopet potujemo po indeksih ležeče besede. Če se nahajamo pri indeksu, kjer prva ali druga pokončna beseda sekata ležečo, zapišemo ustrezno črko, če ne pa piko. Za vsako zapisano črko se spet zmanjša dolžino ustrezni besedi za ena.
Da ugotovimo, katero črko moramo zapisati pri kateri besedi, moramo preveriti, katero besedo smo začeli zapisovati prvo. Pri tisti, ki smo jo začeli zapisovati prvo, samo nadaljujemo z indeksom vrstice, pri katerem smo ostali v prejšnjem koraku. Pri drugi besedi pa začnemo šteti od začetka (od prve črke naprej) in moramo trenutnemu indeksu vrstice odšteti toliko, kot je bilo zgornjih vrstic s črkami iz ene besede.
Reševanje problema (izpis rešitve)
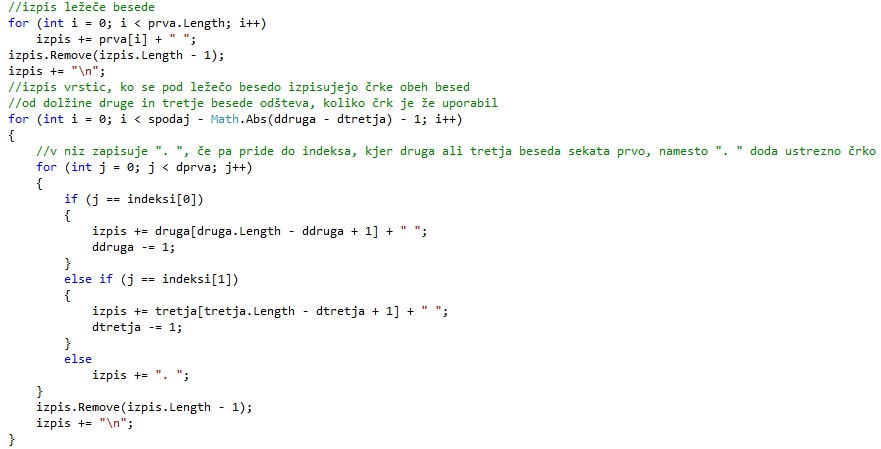
Potem zapišemo vrstico z ležečo besedo in vrstice pod ležečo besedo z obema pokončnima besedama.
Vrstic z obema pokončnima besedama je toliko, da številu vrstic, ki so spodaj, odštejemo absolutno razliko dolžin preostanka pokončnih besed. V vsaki vrstici potem spet potujemo po indeksih ležeče besede in preverjamo, če moramo rešitvi dodati ustrezno črko ali piko. Ob vsaki zapisani črki ustrezni besedi tudi zmanjšamo preostalo dolžino. Indeks črke, ki jo moramo zapisati pa dobimo tako, da dolžini celotne pokončne besede odštejemo njeno preostalo dolžino
Reševanje problema (izpis rešitve)
Zpisati moramo še zadnje vrstice, kjer se nahajajo črke samo ene pokončne besede. Teh vrstic je maksimum od preostanka dolžin obeh besed. Ne smemo pozabiti tudi, da ko smo zapisali ležečo besedo, tega nismo upoštevali pri doližini pokončnih besed.
Če nam ostane za zapis prva pokončna beseda, zadnje vrstice zapisujemo spet tako, da potujemo po indeksih ležeče besede. In ko pridemo do indeksa, kjer ta beseda seka ležečo, za pišemo črko, drugače piko.
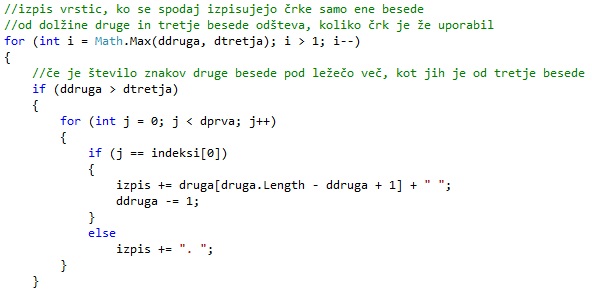
Enako naredimo, če nam ostane za zapis druga pokončna beseda.
Tako dobimo rešitev za izpis.
Testiranje programa