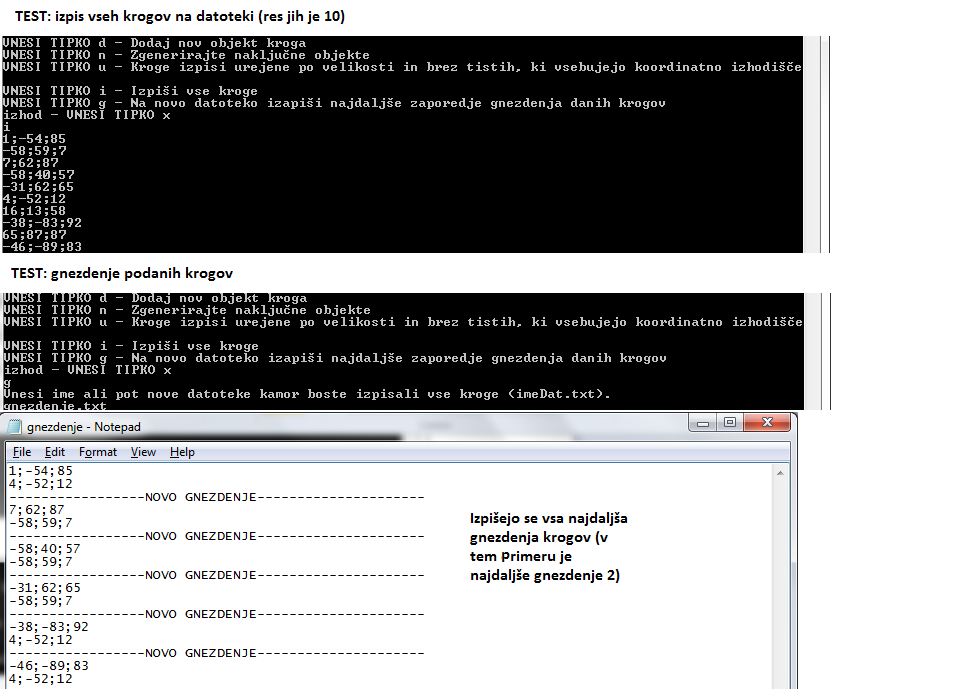
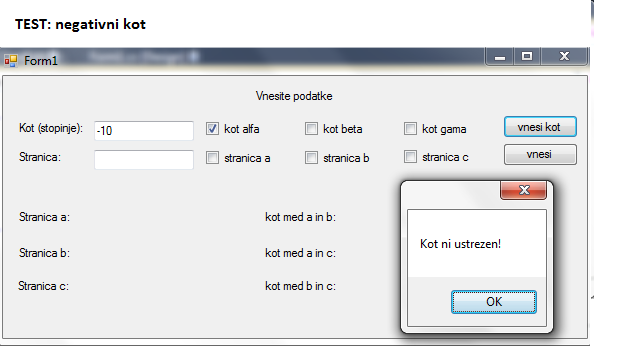
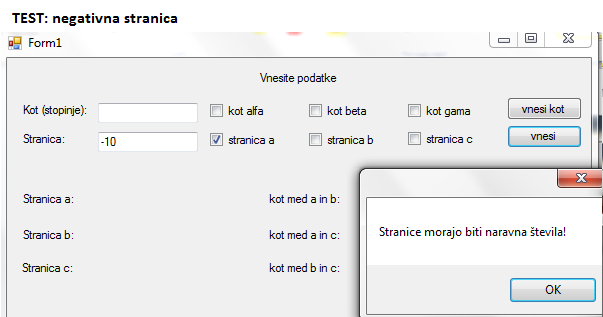
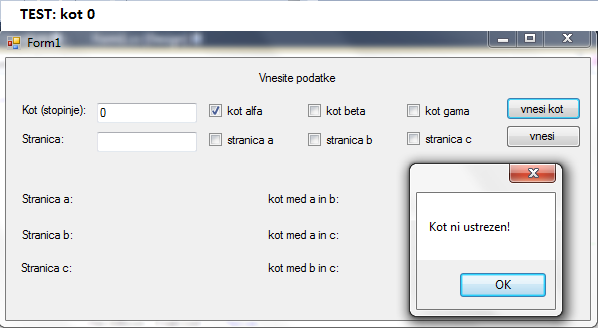
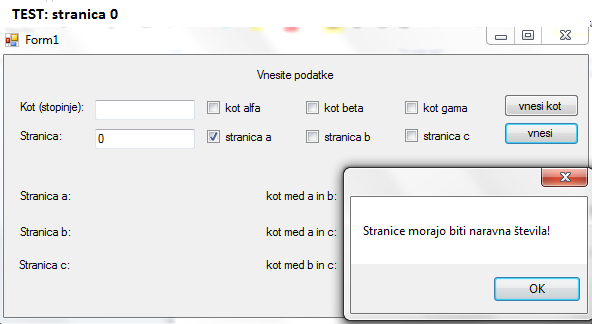
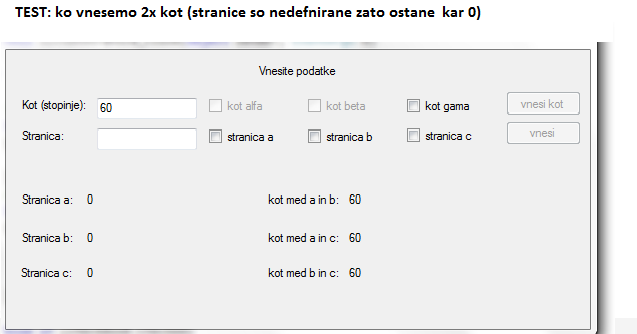
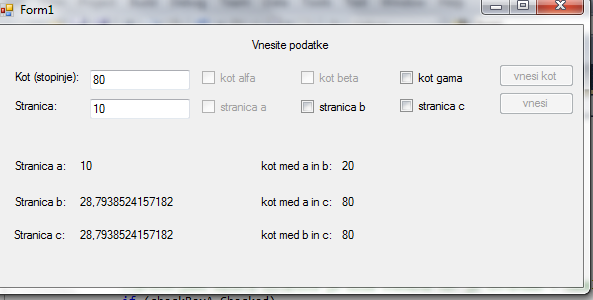
IDEJA:

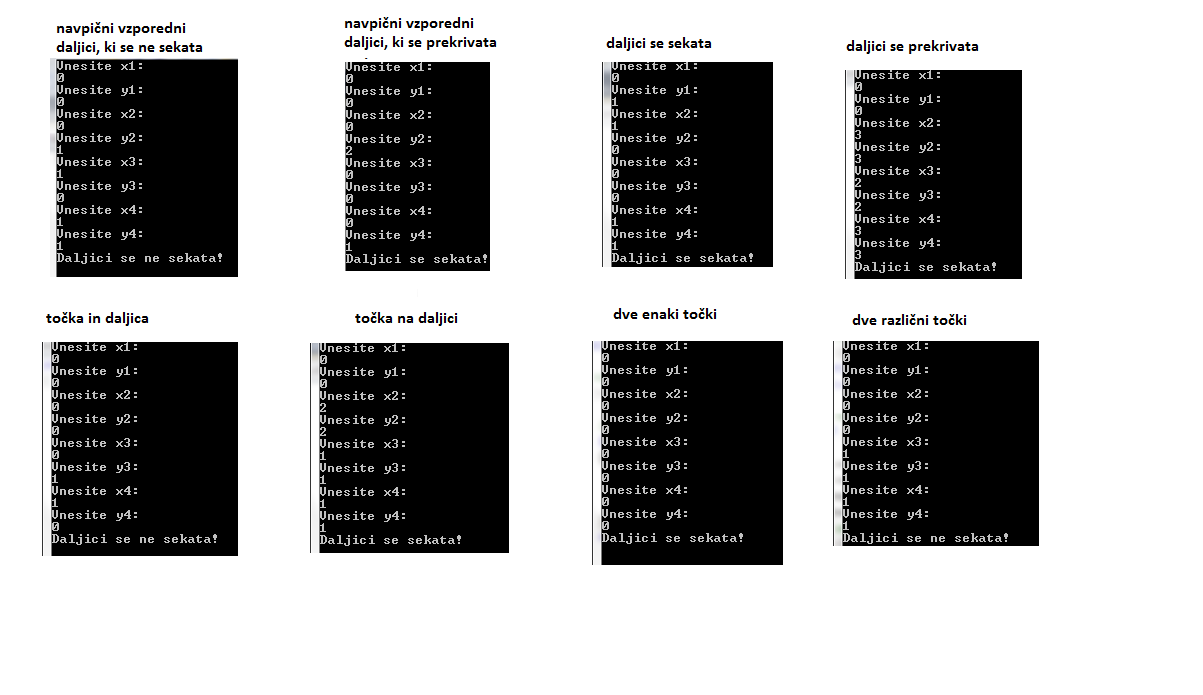
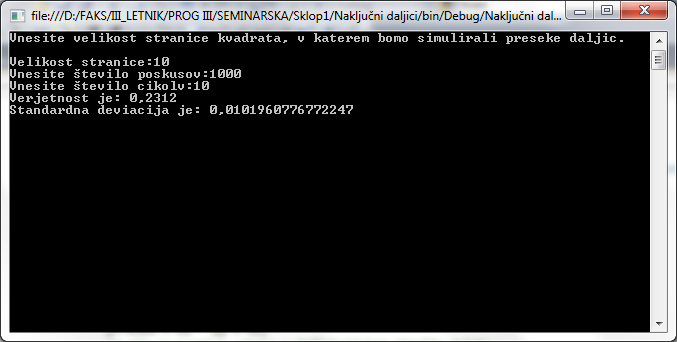
Naloga od nas zahteva, da sestavimo program, ki nam bo izračunal kakšna je verjetnost, da se dve poljubni daljici v nekem kvadratu sekata. Če premislimo, ugotovimo da verjetnost ne bo odvisna od velikosti stranice kvadrata, saj sta daljici v kvadratu naključni. Spomnimo se, da premico določata dve točki, torej bomo potrebovali za dve premici zgenerirati 4 naključne točke. Ker se vse dogaja v 2D prostoru bo točka imela dve naključni koordinati x in y, ki bosta v ustreznem rangu kvadrata (morata biti vsebovani v kvadratu). Torej zgenerirati bomo morali 4 točke z naključnima koordinatama x in y, da bomo določili dve daljici. Sedaj bomo morali še ugotoviti ali se premici sekata. Če skozi daljici potegnemo premico, vemo da se premici zagotovo nekje sekata če nista vzporedni. Tako dobimo idejo, da zapišemo enačbi dveh premic in poiščemo presečišče (če se sekata) te nato preverimo ali se nahaja na ustreznem deginicijskem območjo obeh daljic. Če definicijsko območje v točki presečišča obstaja, potem smo ugotovili, da se daljici sekata. Da dobimo verjetnost preseka daljic večkrat ponovimo postopek in pogledamo kolikokrat od vseh poskusov se naključni daljici sekata od vseh poskusov. Več poskusov kot naredimo bolj točna bo verjetnost. Za izračun standarden deviacije pa le ustrezno formulo (potrebovali bomo izračunati še povprečje vseh ciklov, ki smo jih opravili).

ALGORITEM:

Naš program bo sestavljen iz konzolne aplikacije in knjižnice. V konzolni aplikaciji bomo uporabniku omogočili vnos velikosti stranice kvadrata, število poskusov in število ciklov. Tu bomo tudi naključno generirali 4 točke v rangu danega kvadrata, ki bodo predstavlale dve daljici. V knjižnici pa bomo napisali funkcijo, ki bo za naključno zgenerirani daljici v kvadratu ustrezne velikosti preverila ali se sekata. Funkcija bo za parametre sprejemala sprejela vse koordinate 4 točk. Funkcija bo vračala true ali false. V fnkciji bomo preverili vse možnosti kako so lahko daljice postavljene.

• Preverimo ali sta daljici navpični (to pomeni, da ko bi računali koeficient ustreznih premic skozi daljice bi dobili za koeficient napako – koeficient je neksončno). Če sta navpični se ne sekata razen če ležita na enakem x in se prekrivata na y območju.
• Preverimo je ena izmed daljic navpična (dve možnosti- ali prva ali pa druga). Naračunamo koeficient daljice, ki ni navpična in izračunamo presek premic skozi daljici. Ko dobimo točko preseka, preverimo ali leži v x in y območju obeh daljic. Če leži, potem se daljici sekata.
• V primeru, da nobena izmed daljic ni navpična, lahko brez problema za vsako daljico naračunamo koeficient in tako poiščemo presečišče. Tako kot pri točki 2. potem preverimo ali presečišče leži v x in y območju obeh točk. Če leži potem se daljici sekata, drugače pa ne.

Tako smo napisali funkcijo, ki preveri ali se dve daljici sekata. Sedaj le v konzolni alplikaciji zgeneriramo dve daljici in preverimo ali se premici sekata. Ta postopek ponovimo tolikokrat, kolikor bo uporabnik zahteval v konzolni aplikaciji. Ko to naredimo izračunamo verjetnost, da se premici sekata v kvadratu (št. Poskusov kjer se sekata/vsi poskusi).

Temu postopku pravimo en cikel. Cikolv pa opravimo tolikokrat kolikor bo zahteval v aplikaciji uporabnik. Med vsemi cikli izračunamo povprečno verjetnost in standardno deviacijo.

Opazimo, da je verjetnost sekanja premic enaka, neglede kako velik je kvadrat. Več poskusov in ciklov naredimo bolj točna je verjetnost in manjša je standardna deviacija.

TESTI:

Kot smo že napisali, smo preverili vse sumljive podatke, ki se lahko pojavijo pri generiranju daljic (navpične daljice, točke,...). Izognili smo se računanju koefcienta in tako deljenju z nič, tako da ne more priti do napak.

description of the image

REZULTAT:

description of the image

IDEJA:

Pri tej nalogi bomo ustvarili eno knjižnico v kateri bomo skonstruirali razred krog in vse ustrezne metode, ki jih bo ta razred potreboval. Ustvarili bomo tudi konzolno aplikacijo v kateri bomo testirali naš razred krog in vse njene metode.

Najprej bomo v knjižnici ustvarili nov razred Krog. Tukaj bomo definirali vse privatne in javne spremenljivke, ki bodo predstavljale lastnosti objektov razreda Krog. Napisali bomo prazni konstrutkor, polni konstruktor in konstruktor, ki ustvari objekt kroga s niza.

Napisali bomo vse metode, ki jih bomo potrebovali za branje objektov z datotek, zapisovanje objektov na datoteko,...

Napisali bomo metodem ki se bodo izvajale nad objekti (obseg, ploščina,...). Dodali bomo še metodo, ki nam bo povedala, ali nek krog leži v drugem krogu. Ta metoda nam bo prišla prav pri iskanju največjega zaporedja gnezdenj. Napisali bomo tudi metodo, ki nam bo objekte krog zapisalo v tabelo in sicer urejene po velikosti. Vse te metode bomo uporabili v konzolnem oknu, kjer bo lahko uporabnik ustvaril objekt kroga, ga zapisal na datoteko...

ALGORITEM:

Večina teh metod ni težka za napisati zato bom le te izpustil.

Metoda LeziV Poglejmo si kako napisati metodo, ki preveri ali je nek krog vsebovan v drugem. To naredimo tako, da preverimo ali je radij večjega kroga večji od vsote radija manjšega kroga in razdalje med središčema krogov. Če to velja potem je manjši krog vsebovan v večjem. V nasprotnem primeru krog ni vsebovan.

Metode za izpis kroga Tukaj smo povozili ToString metodo in definirali kako naj se naš objekt krog izpisuje, ko ga pretvorimo v niz. Ta metoda je zelo pomembna, saj jo bomo uporabljali pri zapisovanje objektov na datoteko.

Metode z datotekami Napisali bomo metode, ki nam bodo dodale objekt krog na datoteko oz. Objekte z datoteke prebrale (v tabelo). Napisali bomo tudi metodo, ki bo na datoteko zapisalo n naključno generiranih objektov krog. Pri vseh metodah, ki bodo na datoteko zapisovale objekte bomo uporabili ToString metodo za izpis objekta. Te metode bodo potrebovale parameter, ki bo definiral kam zapisati objekte oz. s kje jih brati. Metoda za urejanje po velikosti To metodo bomo skonstruirali tako, da se bomo sklicevali na lastost objekta radij. Objekte bomo nato s pomočjo dveh for zank uredili po velikosti

Metoda za iskanje najdaljšega gnezdenja To metodo bomo skonstruirali tako, da si bomo v pomoč definirali nekaj pomožnih funkcij.

Napisali bomo statično funkcijo, ki nam bo ustvarila slovar, ki bo za ključ imel vse objekte krog, ki smo jih ustvarili. Kot vrednost pa bo imel seznam objektov krog, ki so v objektu krog, ki predstavlja ključ vsebovani. Slovar=[k1:[k4,k7,k12], k2:[k6,k7,k11,k13],...] Ta slovar bomo uporabili kot parameter v novi funkciji, ki bo z rekurzijo porovala po vseh možnih poteh gnezdenja. Ta funkcija bo potrebovala za parameter še seznam krogov po katerih bomo gledali gnezdenje.

Funkcija bo najprej s for zanko potovala po vseh ključih seznama, in v zanki za vsak ključ izvedla rekurzivno funkcijo z enakim slovarjem, a drugačnim seznamom krogov. Za seznam krogov bomo uporabili kar vrednost slovarja pri danem ključu. Z tako rekurzijo bomo pregledali vse možne poti. Vsakih ko bomo pri rekurziji šli v globino si bomo objekt krog, ki predstavlja ključ zapomnili, tako da ga bomo dodali v nek seznam, ki ga bomo vodili skozi vse rekurzije. Moj algoritem vodi tak seznam kar v parametrih funikcije. Ko pridemo v globino kjer ključ nima več nobene vrednosti (seznam vsebovanih krogov je prazen), bomo rekurzijo zaključili in dodali seznam gnezdenja v nov seznam ,ki ga razvno tako vodimo skozi rekurzijo (to bo seznam v katerem hranimo vse sezname gnezdenj krogov). Ko se funkcija konča le pregledamo katero je najdalje gnezdenje in le tega izpišemo na želeno datoteko z ustrezno funkicjo.

TESTI:

description of the image

description of the image

IDEJA:

Naš program bo sestavljen iz GUI forme in knjižnice. Forma bo uporabniku omogočala vnašati podatke o trikotniku, knjižnica pa bo vsebovala vstrezno metodo, ki bo dani trikotnik rešila in vrnila podatke o trikotniku.

GUI:

Za vnos kota in stranic sem uporabil vnosna okna in check boxe s katerimi določimo kateri kot oz. stranica je mišljena. Za vnos podatkov imamo na voljo gumb. Pri vsakem vnosu ustrezni kot oz. stranica izgine, kar pomeni da njene vrednosti ne moremo več spreminjati.

KNJIŽNICA:

Ko vnesemo podatke s pomočjo GUI le te uporabimo v funkciji iz knjižnice, ki nam reši trikotnik. Rešen trikotnik nato na GUI formi izpišemo.

ALGORITEM:

V razredu forme inicializiramo tabelo, ki sprejema podatke tipa Double. Tabela bo dolžine 6. V njo bomo shranjevali podatke o trikotniku, ki jih bo uporabnik vnesel preko GUI. Privzeta vrednost vsakega elementa tabele je kar 0.

TABELA: [stranica a,stranica b,stranica c, kot alfa, kot beta, kot gama]

V knjižnici definiramo tako funkcijo, ki sprejme to tabelo in ustrezno dopolni iskane vrednosti glede na podatke, ki jih je podal uporabnik.

Tu si pomagamo s sinusnim in kosinusnim izrekom ter kotnimi funkcijami.

Ko izračunamo manjkajoče vrednosti te izpišemo na GUI formo in tako rešimo trikotnik.

Da bomo lažje računali mankajoče vrednosti si bomo v knjižnisi definirali še dve fnkciji, s katerima bomo spreminjali stopinje v radiane in obratno.

TESTI:

description of the image

description of the image

description of the image

description of the image

description of the image

description of the image