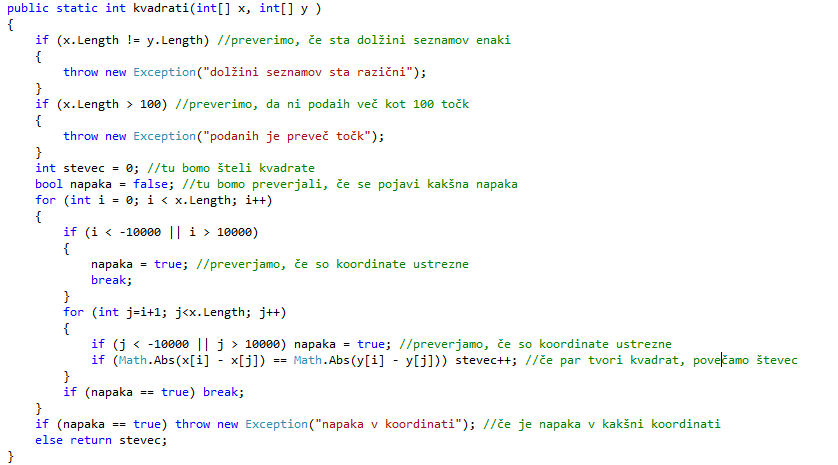
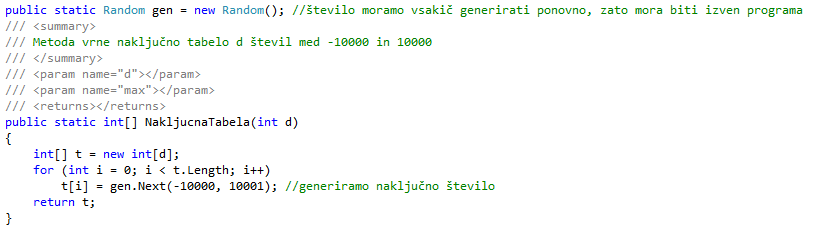
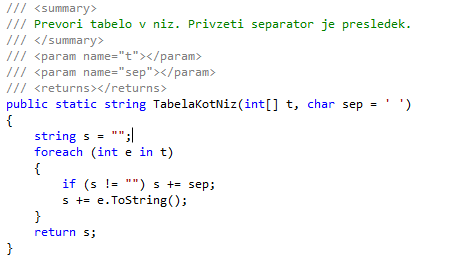
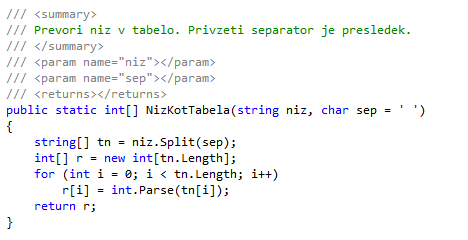
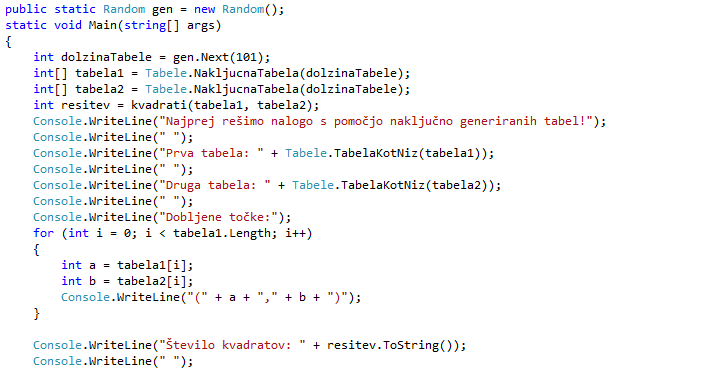
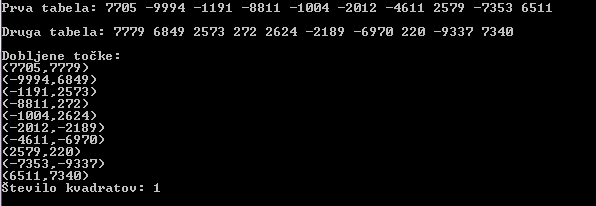
Podane so celoštevilske koordinate n točk, ki ležjo v ravnini. Vsak par teh točk določa pravokotnik, ki ima s koordinatnima osema vzporedne stranice in ena točka leži v njegovem spodnjem levem oglišču, druga pa v zgornjem desnem oglišču. Napiši program, ki učinkovito poišče število takih pravokotnikov, ki so kvadrati. Štej tudi izrojene kvadrate, pri katerihspodnje levo in zgornje desno oglišče sovpadata. Število točk n je največ 100. Območje, na katerem ležijo točke v ravnini, je znotraj kvadrata:

• 10 000 ≤ x ≤ 10 000,
• 10 000 ≤ y 10 000

Najprej preverimo, če so vnešeni podatki uporabnika korektni, se pravi, če sta dolžini seznamov enaki ter da ni podanih več kot 100 točk. Nato ustvarimo števec, katerega bomo povečali, če program najde kvadrat, ter bool spremenljivko, ki bo preverjala, če so točke v pravih mejah. Za vsak par točk pregledamo, če je absolutna vrednost razlike abscis enaka absolutni vrednosti razlike ordinat. Če ta enakost velja, potem imamo kvadrat in števec povečamo.

Program za vhodna podatka dobi dve tabeli števil. V programu najprej preverimo, če sta dolžini seznamov enaki (da sploh lahko tvorimo točke), ter da ni podanih več kot 100 točk. Če podatki niso vredu, potem program vrže izjemo. Nato ustvarimo števec, s katerim bomo šteli kvadrate, ter logično spremenljivko, s katero bomo preverjali, da ne pride do napake (da so koordinate točk pravilne). Dokler ne pregledamo vseh parov točk, pregledujemo, če je absolutna vrednost razlike abscis enaka absolutni vrednosti razlike ordinat. Če ta enakost velja, potem imamo kvadrat in števec povečamo. Če smo kje na poti naletili na napako, potem program vrže izjemo, sicer pa program vrne števec, ki nam pove koliko kvadratov imamo.
Koda v c#:

Pri reševanju testnih primerov sem si pomagala s knjižnico Tabele, kjer sem ustvarila tri različne metode.
Prva metoda vrne naključno tabelo d števil med -10000 in 10000.

Druga metoda prevori tabelo v niz. Privzeti separator je presledek.

Tretja metoda pa prevori niz v tabelo. Privzeti separator je presledek.

Najprej sem naredila dve naključno gernerirani tabeli, ki predstavljata koordinati točk. Tabeli sem uporabila za vhodne podatke našega programa.

koda

izpis rešitve

Nato sem uporabniku omogočila še vnos svojih podatkov.

koda

V testnem primeru sem izbrala točke (1,1), (2,2) ter (3,1).

izpis rešitve

V spodnjem filmčku si lahko pogledate delovanje programa.