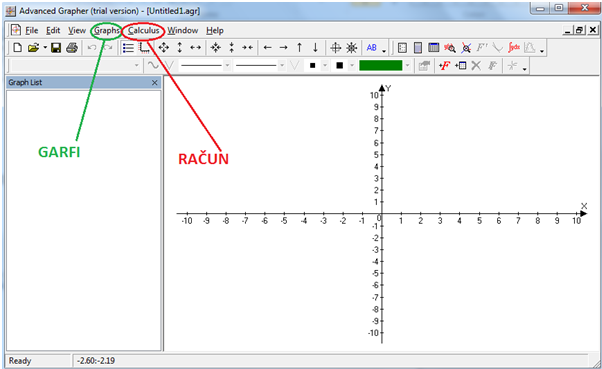
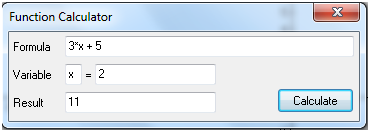
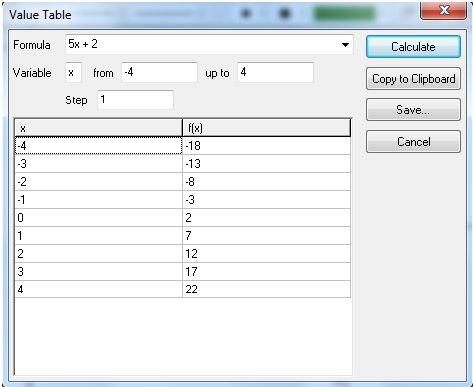
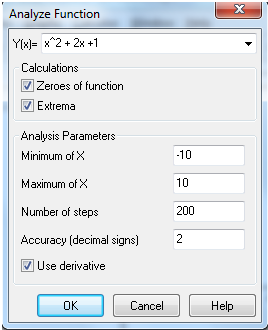
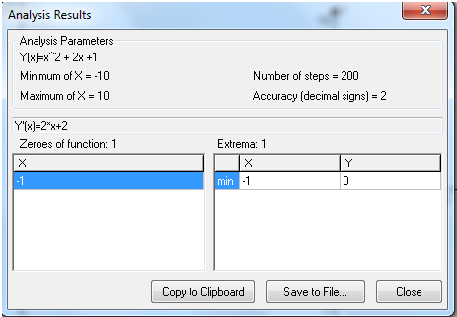
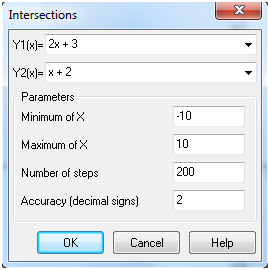
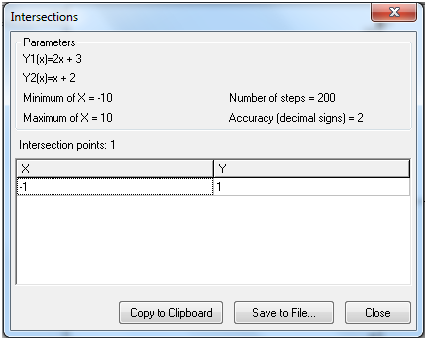
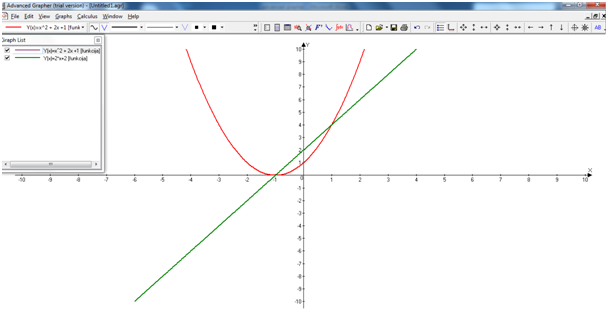
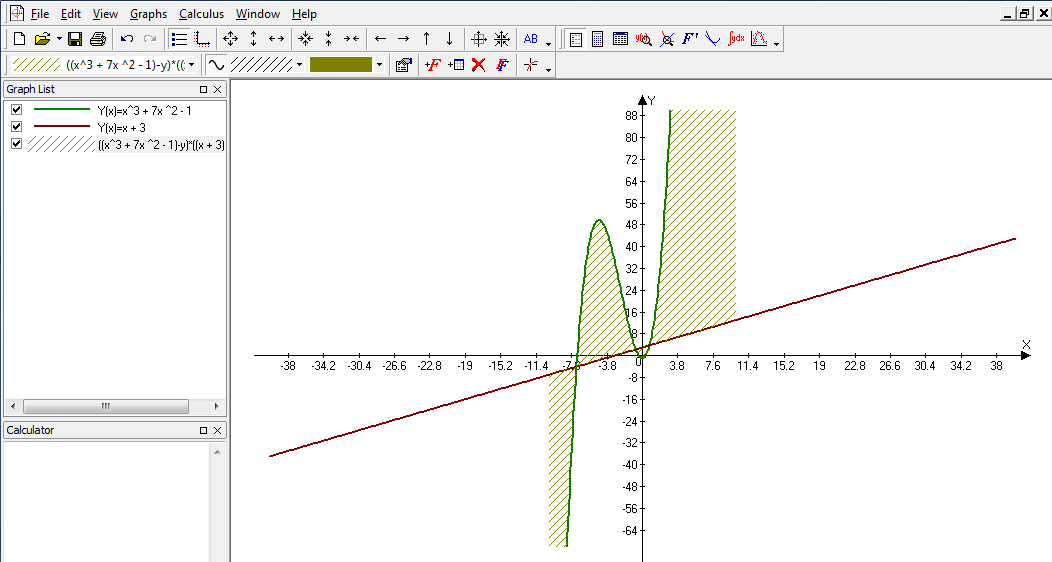
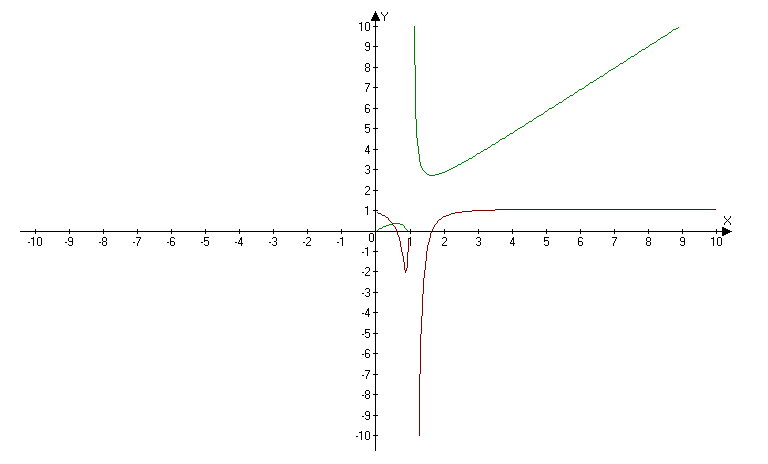
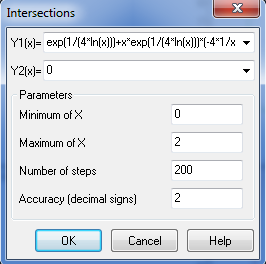
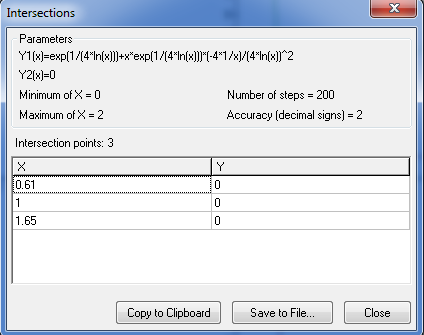
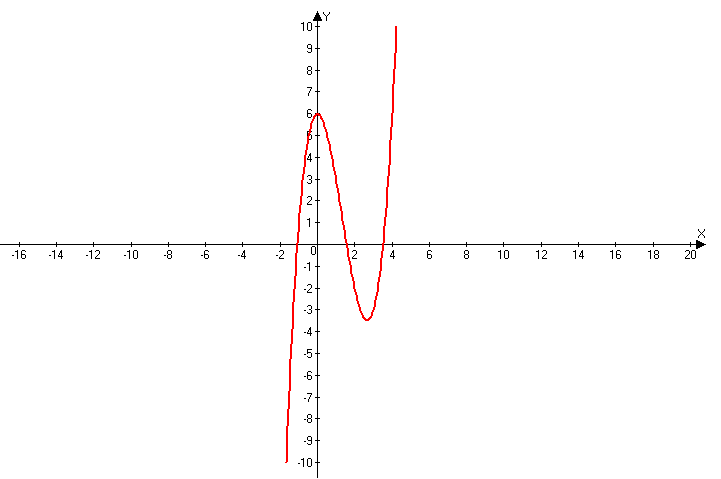
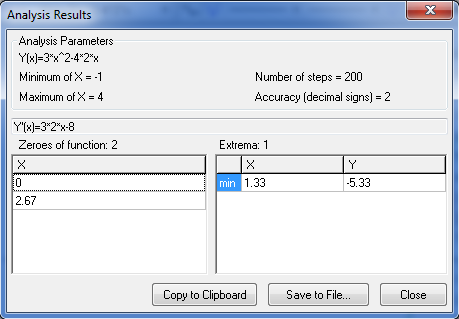
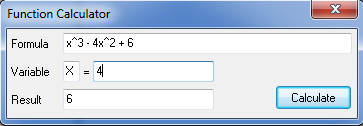
Advanced Grapher je program podjetja Alentum software (Prenos programa) . Gre za plačljiv program s 30 dnevnim brezplačnim preiskusom. Program je namenjen matematičnim operacijam kot so risanje grafov in njihovi analizi, reševanje enačb, neenakosti ter risanje krivulij.

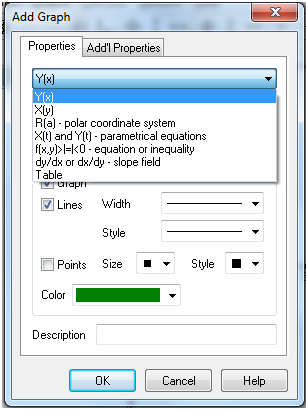
Program ima podprtih več grafičnih oblik:

• Y(x) ali x(y) (inverz)

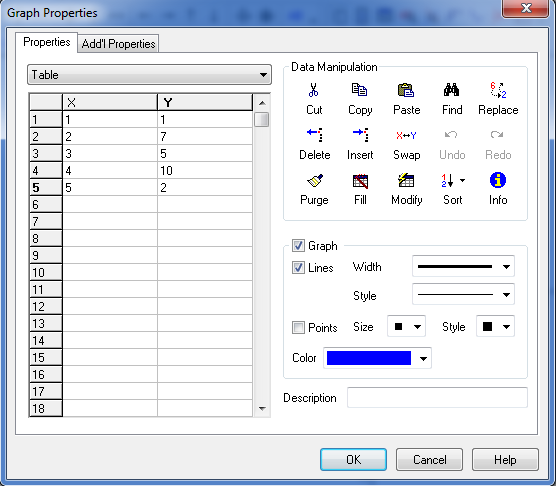
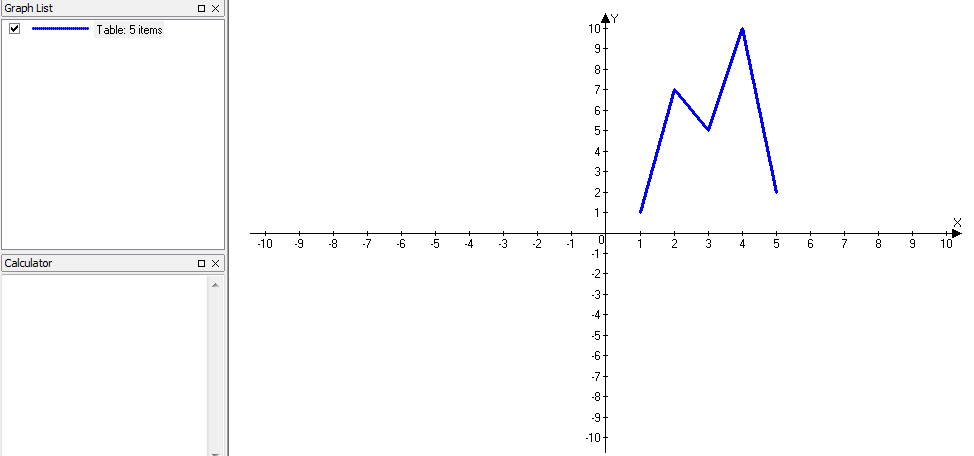
• tabela

• R(a) (polarne koordinate)

• X(t) in Y(t) (parametrične koordinate)

• f(x,y) = 0 (grafi enačb)

• f(x,y) > 0 , f(x,y) > 0 (grafi neenačb)

• dx/dy(x,y) in dy/dx(x,y) (odvodi)

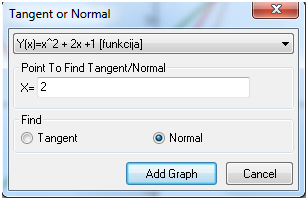
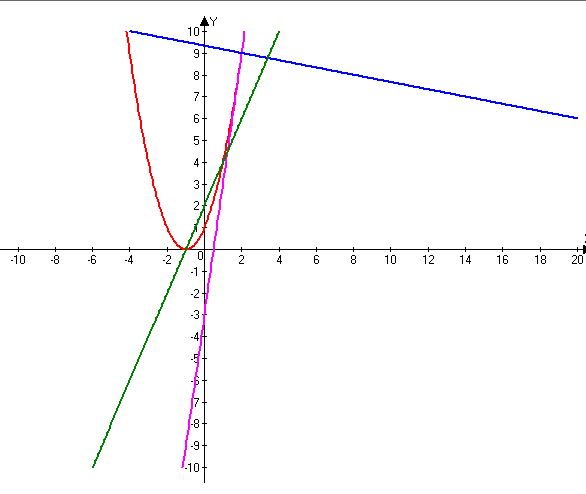
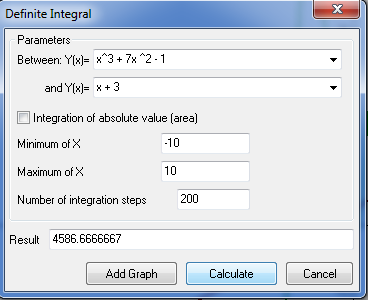
Program uporabniku omogoča tudi spreminjanje barve, sloga in širine črte ter točk in senčenje grafa ter spreminjanje intervala. Omogočeno je dodajanje tekstov in pojasnil na grafu. Izračuna ničle, ekstreme funkcij, odvode (tangente, normale) in integrale. Poleg tega program omogoča izvoz grafa v programe kot je Word, ter njihovo shranjevanje. Program ima tudi večjezični vmesnik.

izgled programa

Poleg ostalih ukazov kot so datoteka, uredi, različne možnosti pogleda ter ukaza pomoč, sta za uporabnika pomembna dva GRAPHS(GRAFI) ter CALCULUS (RAČUN).

V zavihku Calculs so omogočene različne računske operacije.

Če izberemo prvi zavihek Calculator (Računalo), se nam na levi strani okna odpre prostor, v kateremu lahko računamo. Ta omogoča le računanje s števili, če vanj vpišemo enačbo, nam program javi napako.

Za računanje s spremenljivkami uporabimo zavihek Function Calculator. Tu vpišemo funkcijo, ki pa mora biti odvisna le od ene spremenljivke. S pomočjo Function Calculator-ja lahko torej izračunamo vrednost funkcije, pri dani vrednosti neodvisne spremenljivke.

računalo

računalo s spremenljivkami

Program omogoča tudi tabeliranje funkcije.

Izberemo zavihek Value Table.Pojavi se okno v katergav pišemo funkcijo, izberemo spremenljivko, povemo interval spermenljivke ter njen korak. S pritiskom na gumb Calculate izpišemo tabelo z vrednostima ter . Program omogoča tudi shranjevanje tabele.

tabeliranje

Zavihek Intersection nam omogoča računanje presečišča dveh funkcij. Izberemo dve izmed prej vnešenih funkcij(y1 in y2), ter določimo intevral, na katerem bomo iskali presečišče. Dobimo podatke o presečišču

presečišče1

presečišče

Naslednja operacija, ki jo lahko izvedemo na funkciji je tangenta ali normala na krivuljo v dani točki. Ukaz se nahaj v zavihku calculus. Izberemo točko (v tem primeru pri ) v kateri želimo narisati tangento oziroma normalo.

Tangenta(roza) in normala(modra)

V zavihku calculus izberemo odvod (derivate), izberemo funkcijo, ki jo želimo odvajati ter pritisnemo gumb add graph, v oknu se izpiše tudi enačba odvoda.

odvod

Pojavi se okno, kjer lahko spremenimo lastnosti grafa. Nato se v koordinatnio sistem nariše graf odvoda.

odvod graf

V zavihku Calculus izberemo ukaz Integration.

Z ukazom integration lahko izračunamo ploščino, med dvema funkcijama.

Za uporabo ukaza je potrebno imeti definirani dve funkciji. Kliknemo na ukaz Integration, odpre se okno, kjer, lahko izberemo funkciji, med katerima želimo izračunati ploščino. Prav tako v tem oknu omejimo interval.
Če želimo izračunati ploščino, pritisnemo gumb Calculate. V oknu Result se izpiše rezultat.

Če pritisnemo na ukaz Add Graph, lahko graf integracije tudi narišemo.

REŠITEV MATEMATIČNEGA PROBLEMA S POMOČJO PROGRAMA

Analiza 1, finančna matematika 2. Kolokvij ,16.1.2013

Funkcija f je podana s predpisom . Določi definicijsko območje, lokalne ekstreme, intervale naraščanja in padanja, limite na robu definicijskega območja, ter skiciraj graf.

Lokalni ekstremi:

1. V zavihku Graphs izberemo Add graph, ter v vnosno polje vpišemo našo funkcijo ter graf narišemo v koordinatni sistem (zelene barve).
2. Odpremo zavihek Calculus ter izberemo Derivate (odvod). Označimo funkcijo ter dodamo graf odvoda (rdeče barve)

Program omogoča shranjevanje podatkov, ki smo jih izračunali. Pritisnemo gumb Save to file, ter shranimo podatke na datoteko. Če datoteko odpremo vidimo da so se podatki prepisali na datoteko.

Sedaj ko so lokalni ekstremi znani, lahko določimo še intervale naraščanja in padanja. Preberemo jih lahko kar z grafa.

Funkcija torej pada na intervalu med 0.61 ter 1, ter med 1 in 1.65 (pri 1 ni definirana)ter narašča na intervalu med 0 in 0.61 ter 1.65 do neskončno.

Izračunati moramo le še limito na robu definicijskega območja.

Program nima vgrajenje funkcije za izračun limite, vendar jo v danem primeru lahko razberemo iz grafa. Takoj se lahko prepričamo, da je limita ko gre x proti 0 enaka 0, ter ko gre x proti neskončno enaka neskončno. Pregledati moramo še kaj se zgodi, ko gre x proti 1. Opazimo da sta v tej točki tako leva kot desna limita enaki neskončno.

Določi globalne ekstreme funkcije na intervalu [-1,4].

1. V zavihku Grahs izberemo ukaz Add Graphs, izberemo eksplicitno obliko funkcije ter jo vnesemo v okno (Y(x)=x^3-4x^2+6).

Slika funkcije

2. V zavihku Calculus izberemo ukaz Derivate, označimo našo funkcijo ter pritisnemo gumb Add graph.

3. Ničle odvoda določimo s pomočjo ukaza Analyze Function, ki ga najdemo pod zavihkom calculus. Izberemo enačbo odvoda, interval analize omejimo od -1 do 4 ter pritisnemo gumb OK. Pojavi se nam novo okno v katerem so poleg lokalnih ekstremov izračunane tudi ničle. Ničle so x1 = 0, x2 = 2.67

Izračun ničel odvoda

4. Izračunti moramo f(-1), f(0), f(2,67) in f(4). Odpremo ukaz Function calculator. Vpišemo formulo x^3 -4x^2 + 6 ter za x vstavimo različne vrednosti, ter zapisujemo rezultate.
Dobimo:
f(-1) = 1
f(0) = 6
f(2.67) = -3.48
f(4) = 6

Računanje vrednosti

Ker funkcija doseže največjo vrednost pri x = 0 in x = 4, (tu je vrednost funkcije enaka 6) je globalni maksimum enak 6.
Funkcija doseže najmanjšo vrednost pri x = 2.67, torej je globalni minimum enak -3.48.