Igra go. Go je strateška miselna igra na deski za dva igralca. Izvira z Daljnega vzhoda, kjer je še danes najbolj priljubljena. Postopoma pridobiva popularnost tudi v drugih delih sveta. Za igro so potrebni deska ter figure, imenovane kamni, dveh različnih barv - navadno so bele in črne.

Igralna plošča in kamni za go

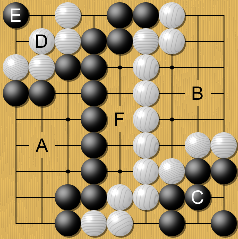
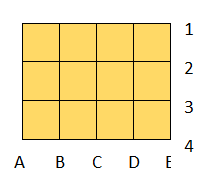
Deska je z vodoravnimi in navpičnimi črtami razdeljena na množico točk (presečišč črt), katerih število je odvisno od želene težavnosti in dolžine igre. Najpogostejše so mere 9×9, 13×13 in 19×19 točk. Igralca med igro izmenično polagata kamne na presečišča. Cilj igre je s svojimi figurami obkrožiti več prostora (tj. praznih presečišč) od nasprotnika.

Prvi začne igro črni, ki lahko svoj kamen položi na katerokoli presečišče. Nato je na vrsti beli igralec, ki lahko svoj kamen položi kamorkoli, razen na že stoječega.

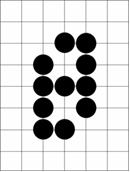
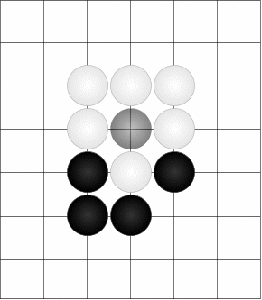
Preprostost teh pravil pokvari pravilo, da mora vsak kamen na deski »živeti«. To pomeni, da mora imeti prosto vsaj eno točko, ki je posredni ali neposredni sosed točke, na kateri leži kamen (veljajo le vodoravne in navpične povezave, na pa diagonalne).

Atari. Kamen je v »atari«, kadar se ga da vzeti z eno potezo. Podobno kot kralj v »šahu« (le da ga tam ne vzamemo). Seveda je možno da je cela skupina kamnov v »atari« - očesa pa igralca zaščitijo pred to situacijo.

Dvojna očesa. S takšno strukturo lahko zaščitimo katerikoli kamen, ki je njen del, saj nasprotnik ne more v eni potezi zavzeti vseh svobod, ne da bi kršil pravila.

Dvojno oko

Verige. Večje skupine medsebojno povezanih kamnov ene barve, ki npr. sekajo desko, obkrožajo nasprotnika ipd. Zaradi svoje velikosti imajo veliko prostosti. Pravimo, da veriga »živi«, če ima vsaj dve, med seboj neodvisni očesi ali pa dovolj »prostora« znotraj sebe, da lahko kadarkoli to naredi. Na spodnji sliki A označuje teritorij črnega, B pa belega. F je nevtralni teritorij. Skupina, kjer je kamen C je uspela oblikovati dvojno oko in bo zato preživela. Kamen E bo prej ali slej mrtev.

Verige

Ko. Slika nakazuje potezo črnega (polprosojno), ki je znana kot »ko«. Črni bo vzel belemu kamnu vse svobode, ga odstranil s plošče in si priboril eno svobodo. Na to potezo bi beli normalno takoj odgovoril s kamnom na istem mestu, a pravila prepovedujejo takšno vrtenje v krogu, zato mora beli igralec kamen postaviti drugam. Beli igralec zato izbere potezo, na katero črni »mora« odgovoriti. Taki potezi rečemo grožnja in naj bi bila ekvivalentna (ali večja) od izgube, če črni na potezo ne odgovori.

Ko

Na kratko

Monte Carlo drevesno iskanje (angl. Monte Carlo Tree Search - MCTS) je metoda za iskanje optimalne odločitve na določeni domeni s pomočjo naključnega jemanja vzorcev iz prostora možnih odločitev in graditev iskalnega drevesa na podlagi dobljenih rezultatov. Torej v neki igri simuliramo naključne poteze, od tod povezava z Monte Carlo metodami. Sosledje izbranih potez nato predstavimo z drevesom.

Čemu motivacija na začetku?

Mini max algoritem ni primeren za igre z velikim t.i. vejitvenim faktorjem (angl. branching factor). Le-ta pomeni število podrejenih vozlišč (otrok), ki vodijo iz izbranega vozlišča. Povedano drugače, kompleksnost (število vseh stanj, pozicij) teh iger je zelo velika. Izkaže se, da je v primeru iger kot je go, Monte Carlo drevesno iskanje boljša izbira.

Pogled na algoritem MCTS od daleč

Teorija odločitev. Združuje teoriji verjetnosti in koristnosti. Omogoča nam ogrodje za odločanje v pogojih negotovosti. Teorija iger. Le-ta je razširitev teorije odločitev v primeru, ko pride do interakcije več agentov (npr. igralcev pri neki igri). Igro definiramo kot zbirko pravil, ki omogočajo interakcijo enega ali več igralcev in s tem povezanih rezultatov oz. dobitkov. Metode Monte Carlo. Te metode imajo svoje korenine v statistični fiziki, kjer jih uporabljajo za izračun približkov analitično nerešljivih integralov, tj. pri numeričnem integriranju. Danes se uporabljajo tudi pri računalniški grafiki in biologiji, uporabni statistiki, v finančne svetu in seveda pri iskanju najboljših potez pri različnih igrah. Problem igralnih avtomatov, angl. »Multi-armed bandit problem«. Na njega naleti hazarder v igralnici, ko je postavljen pred vrsto igralnih avtomatov in se potem sprašuje:

• na katerih avtomatih naj igra;
• kolikokrat naj igra na posameznem avtomatu;
• v katerem vrstnem redu naj igra. Vsak avtomat vrne naključen izid glede na svojo porazdelitev . Te porazdelitve niso znane. Hazarder seveda želi maksimirati svoj seštevek zadetkov.

Kot je že bilo omenjeno na prejšnji prosojnici sak avtomat vrne naključen izid glede na svojo porazdelitev. Te porazdelitve niso znane. Hazarder seveda želi maksimirati svoj seštevek zadetkov. Pri tem je pomembno usklajeno razmerje med pridobivanjem (npr. večkrat eno in isto ročko) in raziskovanjem (katere ročke bi še uporabili?). Tu nastopi izračun UCB za vozlišče v oz. ročko(angl. Upper Confidence Bound). Izračun sta predlagala Levente Kocsis in Csaba Szepesvári.

Prvi člen v vsoti predstavlja izkoristek. Višji je za višje vrednosti vozlišča (ugodnejši položaji v igri). Drugi člen zastopa raziskovanje. Višji je za vozlišča, ki so bila obiskana malokrat, torej malokrat preizkušeni položaji.

Igralni avtomat

Primer drevesa

selection – izbira, expansion – širitev, simulation – simulacija, - backpropagation – povratno poročanje. Številke v krogih predstavljajo razmerje (vrednost vozlišča)/(število obiskov i-tega vozlišča).

Pri obeh vrednostih c-ja bo algoritem izbral 2. vrstico. Vedno se izbere vozlišče z višjo vrednostjo UCB.

Izbira

Začenši s korenom K, izberi najbolj uspešna podrejena vozlišča do lista L. Pri tej izbiri nam pomaga zgoraj omenjeni izračun UCB.

Širitev

Če L ni končno stanje igre, ustvari nobeno, eno ali več novih vozlišč (otrok O), ki vodijo iz L. Izberi en O in začni simulacijo iz L.

Simulacija

Igraj naključno igro iz vozlišča O.

Vzvratno poročanje

Za vsako vozlišče na poti od O do korena K osveži podatke o izidu igre in število igranih iger povečaj za ena. Zgoraj opisani postopek se izvaja vse dokler je znotraj predpisanega časa oziroma prostora. Za tem se lahko izbere bodisi vozlišče, ki ima največje število zmag, bodisi najbolj obiskano vozlišče. Pogosto ti dve izbiri pomenita eno in isto stvar, ne pa vedno.

Spodaj je psevdokoda ene izmed največkrat uporabljenih izvedb algoritma MCTS. Imenuje se UCT.

Kliknite tukaj za grafični ogled postopka

Algoritem UCT je:

• ahevrističen: ena izmed največjih prednosti tega algoritma je ta, da ne potrebuje posebnega znanja o nekem področju, zato ga lahko uporabimo za katerokoli domeno, ki se jo da modelirati s pomočjo drevesa; tudi pri šahu, kjer so se z ustvarjanjem kvalitetnih hevrističnih algoritmov ukvarjali leta, se UCT odreže zelo dobro; posebej uporaben je kot že omenjeno pri igri go, kjer tradicionalni minimax odpove; vendar je treba poudariti, da sodobni programi za go kombinirajo tako različne izvedbe algoritma MCTS, kot tudi specifično znanje o igri; tu nastopi vprašanje, koliko tega znanja dodati v program, da se hitrost izvajanja preveč ne spremeni; hitrost pa je ravno ena izmed prednosti algoritma UCT, ki nima implementiranega znanja;
• ažuren: izid naključne igre se poroča navzgor takoj, zato imamo na vsakem koraku iteracije sveže podatke;
• asimetričen: algoritem favorizira bolj obetavna vozlišča, zato graf postopoma pridobiva asimetrično obliko.

Omejimo se na primer 5x4, na levi je konfiguracija koordinat. Črni je računalnik, ki uporablja algoritem MCTS. Kamne odlagamo na križišča. Dodajamo dva otroka. Ujetih kamnov ni.

Igralno polje

Korensko vozlišče