Pritisnite F11

Iz varnostnih razlogov je mogoče celozaslonski način vključiti samo s pritiskom na gumb F11 na tipkovnici.

Ko ste enkrat v celozaslonskem načinu, ga izključite spet s pritiskom na F11.

Risanje funkcij

Avtor: E-um (vsebinsko), Skupina NAUK (tehnično)

Sodelujoče organizacije

Izvedbo projekta je omogočilo sofinanciranje Evropskega socialnega sklada Evropske unije in Ministrstva za šolstvo in šport. Pri tehnični izvedbi projekta so sodelovali: Fakulteta za matematiko in fiziko Univerze v Ljubljani, Inštitut za matematiko, fiziko in mehaniko in podjetje Hruška d.o.o.

Hvala za ogled gradiva!

Veseli bomo vaših komentarjev. Obiščite nas na www.nauk.si.

Uporabljeni viri

E-um

www.e-um.si

Sodelujoče organizacije

Izvedbo projekta je omogočilo sofinanciranje Evropskega socialnega sklada Evropske unije in Ministrstva za šolstvo in šport. Pri tehnični izvedbi projekta so sodelovali: Fakulteta za matematiko in fiziko Univerze v Ljubljani, Inštitut za matematiko, fiziko in mehaniko in podjetje Hruška d.o.o.

V tem poglavju boš samostojno ponovil vse o funkcijah, prav tako o odvodu in to znanje uporabil pri risanju grafov funkcij.

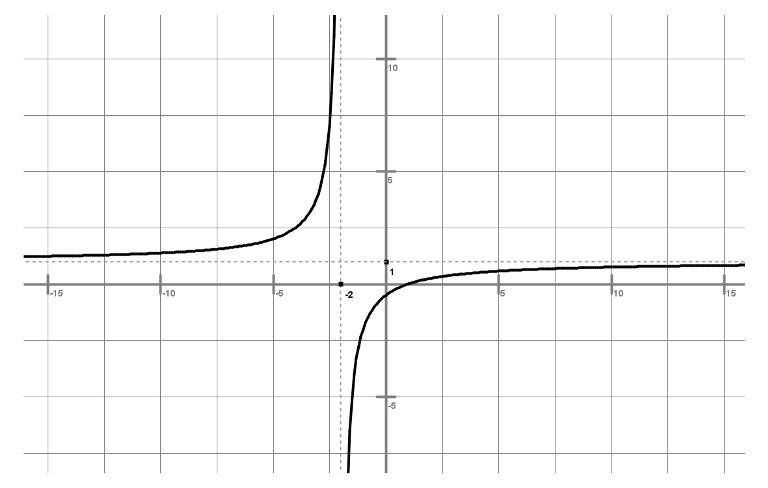
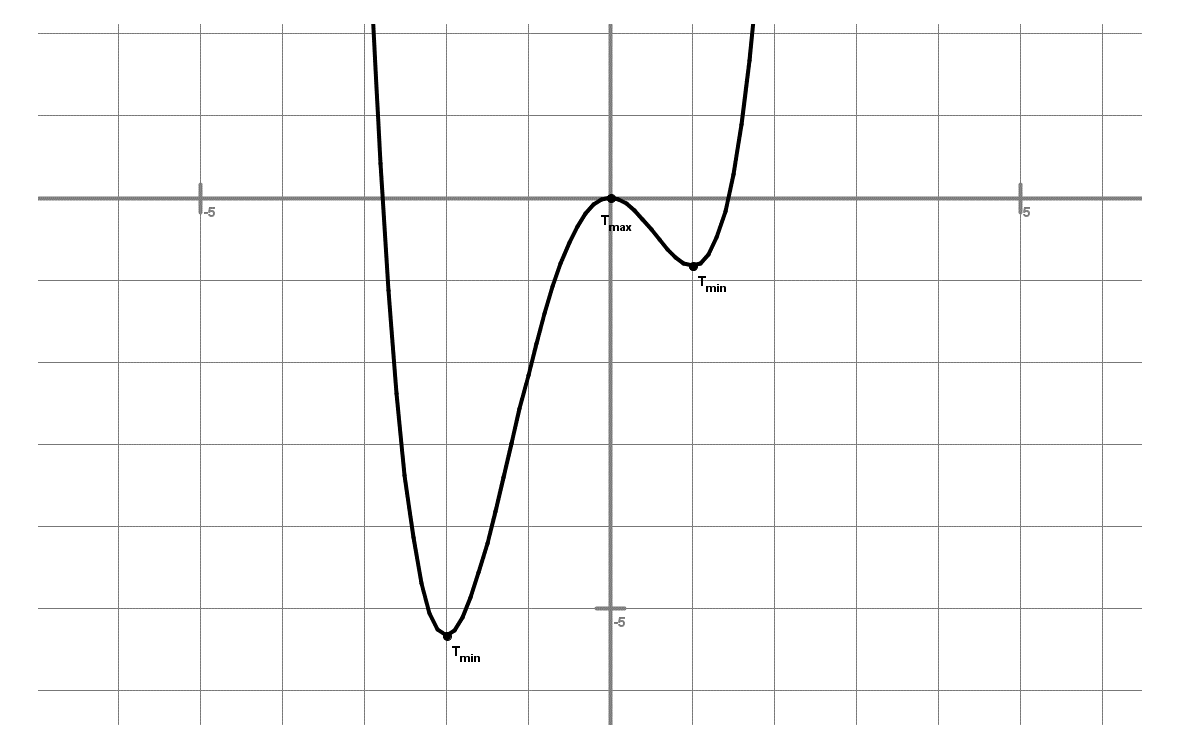
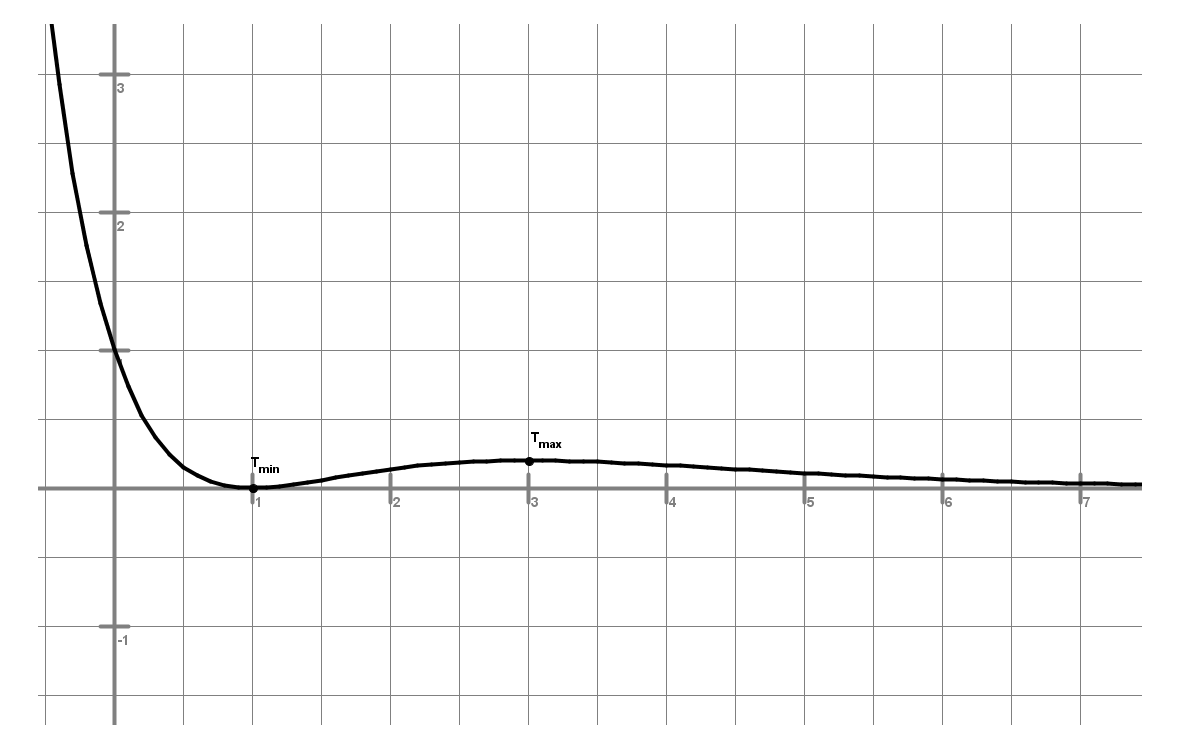
Preden se konkretno lotiš risanja grafa funkcije, je potrebno pridobiti vse podatke, ki dokaj natančno določajo funkcijo in tudi omogočajo, da narišemo graf funkcije. Najprej ponovi, kaj je to definicijsko območje in kaj zaloga vrednosti.

Kratka ponovitev

Dana je funkcija $f(x)$ .

Kaj je definicijsko območje funkcije $f(x)$ ?
Kaj je zaloga vrednosti funkcije $f(x)$ ? Poveži!

Definicijsko območje

Zaloga vrednosti

Počisti

Vsa števila, pri katerih je vrednost izraza $f(x)$ smiselna (izračunljiva).

Vsi elementi, ki so vrednost elementov iz definicijskega območja.

Preveri

Pravilno

Napačno

Poskusi še enkrat.

Slika

Primer

Opazuj graf funkcije na prejšnji sliki in določi definicijsko območje in zalogo vrednosti.

Definicijsko območje je

$\mathbb{R}$

$(-\infty,1) \cup (1,\infty)$

$(-\infty,-2) \cup (-2,\infty)$

Zaloga vrednosti je

$\mathbb{R}$

$(-\infty,-2) \cup (-2,\infty)$

$(-\infty,1) \cup (1,\infty)$

Preveri

Pravilno

Zaloga vrednosti je pravilna, definicijsko območje pa ne.

Pravilno

Definicijsko območje je pravilno, zaloga vrednosti pa ne.

Napačno

Oba odgovora sta napačna. Poskusi še enkrat.

Ničle, poli

Kaj je ničla funkcije?
Ničla funkcije je tista vrednost iz , pri kateri je funkcijska vrednost enaka nič.
$f(x)=0$

Kaj je pol funkcije?
Pol funkcije je tista vrednost, pri kateri $f(x)$ nima smisla.

Ali je za graf funkcije pomembno razlikovati med ničlami (poli) sode oz. lihe stopnje?

NE

DA

Preveri

Pravilno

V okolici sode ničle (pola) funkcije ne spreminja predznaka, v okolici lihe ničle (pola) pa funkcija spremeni predznak.

Napačno

Še enkrat poskusi.

Rešitev

Ničla funkcije je tista vrednost iz definicijskega območja, pri kateri je funkcijska vrednost enaka nič.

Pol funkcije je tista vrednost, pri kateri funkcijska vrednost $f(x)$ nima smisla.

V okolici sode ničle (pola) funkcije ne spreminja predznaka, v okolici lihe ničle (pola) pa funkcija spremeni predznak.

Primer

Dana je funkcija $f(x)=\frac{x^2-1}{x^2(x+2)}$ . Določi ničle, pole, ter definicijsko območje in zalogo vrednosti.

Prva ničla $x=$ je stopnje.
Druga ničla $x=$ je sode lihe stopnje.

Prvi pol $x=$ je stopnje.
Drugi pol $x=$ je sode lihe stopnje.

Definicijsko območje

Zaloga vrednosti

Počisti

$(-\infty,-2) \cup (-2,0) \cup (0,\infty)$

$(-\infty,\infty)$

$1$

$2$

Preveri

Pravilno

Napačno

Nekje si se zmotil. Poskusi še enkrat.

Rešitev

Ničle: $-1$ , $1$ obe lihi stopnji.

Poli: $0$ soda stopnja, $-2$ liha stopnja.

Definicijsko območje: $(-\infty,-2) \cup (-2,0) \cup (0,\infty)$ .

Zaloga vrednosti: $(-\infty,\infty)$ .

Asimptota

Asimptoto si prvič srečal pri racionalnih funkcijah in jo tam tudi obravnaval. Na primeru funkcije $f(x)=\frac{x^2-1}{x+3}$ določi asimptoto.

Asimptota je enaka $y=$ .

Preveri

Za natančen graf funkcije potrebuješ še ekstreme. Te pa kot se spomniš iz prejšnjih poglavij dobiš s pomočjo prvega odvoda funkcije.

Pravilno

Tako je. Asimptoto racionalne funkcije dobiš z deljenjem.

Napačno

Poskusi še enkrat.

Rešitev

Asimptoto racionalne funkcije dobiš z deljenjem. Asimptota je enaka $y=x-3$ .

O pomenu odvoda

Preberi spodnje odstavke in jih dopolni.

Odvod v dani točki nam pove naklonski , ta pa naraščanje oziroma padanje funkcije. Če je odvod v dani točki pozitiven, potem funkcija , če je odvod negativen, potem funkcija . Ničle prvega odvoda imenujemo in so možni ekstremi funkcije. V stacionarnih točkah so tangente z $x$ -osjo.

Preveri

Pravilno

Napačno

Še enkrat poskusi.

Rešitev

Odvod v dani točki nam pove naklonski kot tangente, ta pa naraščanje oziroma padanje funkcije. Če je odvod v dani točki pozitiven, potem funkcija narašča, če je odvod negativen, potem funkcija pada. Ničle prvega odvoda imenujemo stacionarne točke in so možni ekstremi funkcije. V stacionarnih točkah so tangente vzporedne z $x$ -osjo.

Ničle funkcije in njenega odvoda

Za analizo funkcij je uporabna tudi naslednja lasnost, ki jo bomo pokazali. Če ima funkcija ničlo stopnje $k$ ( $k>1$ ), potem ima prvi odvod isto ničlo stopnje $k–1$ .

Naj bo $p(x)=(x-x_0)^k \cdot q(x)$ . Izračunaš odvod po pravilu zmnožka in dobiš $p´(x)=(x-x_0)^{k-1} \cdot (k \cdot q(x)+(x-x_0)q´(x))$ .

Preizkusi se

Funkcija ima ničlo sode stopnje. Izračunaj odvod te funkcije in opazuj ničlo.

V tej točki funkcija nima estrema.

Funkcije se dotika x osi in v njej ni ekstrema.

V tej točki ima funkcija vedno ekstrem.

Zdaj, ko si pravilno razumel pomen večkratnih ničel, ti je najbrž jasno, da pri funkciji, ki ima ničle lihe stopnje večje od $1$ , v teh ničlah ni možnih ekstremov.

Pravilno

Pravilno. Odvod v okolici ničle spremeni preznak iz česar sledi, da je v tej točki možen ekstrem.

Napačno

Poskusi še enkrat.

Naloga 1

Določi ničle, presečišče z $y$ -osjo, stacionarne točke ter ekstreme ter nariši polinom $p(x)=\frac{1}{2}x^4+\frac{2}{3}x^3-2x^2$ . Dopolni rešitev naloge.

Rešitev
Ničle: (druge stopnje), $\frac{-2 \pm 2\sqrt{10}}{3}$ .
Presečišče z $y$ -osjo: $T(0,$ $)$ .
Stacionarne točke: $p´(x)=2x^3+2x^2-4x$ ; $x_1=$ , $x_2=$ , $x_3=$ .
Ker je 0 ničla sode stopnje, pomeni, da je v tej točki prav gotovo ekstrem, ugotoviti je potreben samo kakšen. Ker sta tudi ostali stacionarni točki lihe stopnje, je v njiju prav gotovo ekstrem.
Minimum: $x_1=$ , $x_2=$ ; $T(-2, -\frac{16}{3})$ , $T(1, -\frac{5}{6})$ .
Maksimum: : $T(0,0)$ .

Podrobneje si oglej na naslednji strani.

Preveri

Polinom-slika

Pravilno

Napačno

Poskusi še enkrat. Nekje si se zmotil.

Rešitev

Ničle: $0$ (druge stopnje), $\frac{-2 \pm 2\sqrt{10}}{3}$ .
Presečišče z $y$ -osjo: $T(0,0)$ .
Stacionarne točke: $p´(x)=2x^3+2x^2-4x$ ; $x_1=-2$ , $x_2=0$ , $x_3=1$ .
Ker je 0 ničla sode stopnje, pomeni, da je v tej točki prav gotovo ekstrem, ugotoviti je potreben samo kakšen. Ker sta tudi ostali stacionarni točki lihe stopnje, je v njiju prav gotovo ekstrem.
Minimum: $x_1=-2$ , $x_2=1$ ; $T(-2, -\frac{16}{3})$ , $T(1, -\frac{5}{6})$ .
Maksimum: $0$ : $T(0,0)$ .

Naloga 1

Aplikacija RiŠ se ni mogla zagnati. Prosim preverite, ali imate v brskalniku namescen program Java 1.4.2 (ali novejsi) (Kliknite tu za namestitev Jave)

Riš datoteka

Naloga 2

Določi ničle, asimptoto, stacionarne točk, ekstreme ter nariši funkcijo $f(x)=\frac{(x-1)^2}{e^x}$ . Dopolni!

Ničla je pri $x=$ , asimptota je kar $x$ -os. Stacionarni točki ima dve, in sicer $x_1=$ in $x_2=$ . Prvi je maksimum minimum , drugi je maksimum minimum . Za določitev tega si lahko pomagaš z grafom odvoda dane funkcije.

Preveri

Graf funkcije

Pravilno

Napačno

Poskusi še enkrat. Nekje si se zmotil.

Rešitev

Ničla je pri $x=0$ , asimptota je kar $x$ -os. Stacionarni točki ima dve, in sicer $x_1=1$ in $x_2=3$ . Prvi je minimum, drugi je maksimum. Za določitev tega si lahko pomagaš z grafom odvoda dane funkcije.

Risanje funkcij

Vaš brskalnik je zastarel

Pritisnite F11

Risanje funkcij

Avtor: E-um (vsebinsko), Skupina NAUK (tehnično)

Sodelujoče organizacije

Hvala za ogled gradiva!

Veseli bomo vaših komentarjev. Obiščite nas na www.nauk.si.

Uporabljeni viri

Sodelujoče organizacije

Pravilno

Napačno

Pravilno

Pravilno

Pravilno

Napačno

Pravilno

Napačno

Rešitev

Pravilno

Napačno

Rešitev

Pravilno

Napačno

Rešitev

Pravilno

Napačno

Rešitev

Pravilno

Napačno

Pravilno

Napačno

Rešitev

Pravilno

Napačno

Rešitev