| Spoznali bomo "recept" za določanje največjega skupnega delitelja dveh števil. |
Uvod
| Spoznali bomo "recept" za določanje največjega skupnega delitelja dveh števil. |
Razlaga osnovnih pojmov
| ALGORITEM - po korakih določen postopek, kako se nekaj dela; recept EVKLID - eden največjih grških matematikov (325 pr.n.št. - 265 pr.n.št.) EVKLIDOV ALGORITEM - postopek za določanje največjega skupnega delitelja dveh števil |
Evklidov algoritem
Najprej si oglejmo, kakšen je Evklidov recept za določanje največjega skupnega delitelja. Ko bomo algoritem obvladali, bomo poskušali o njem povedati še kaj več.
Več o Evklidovem algoritmu
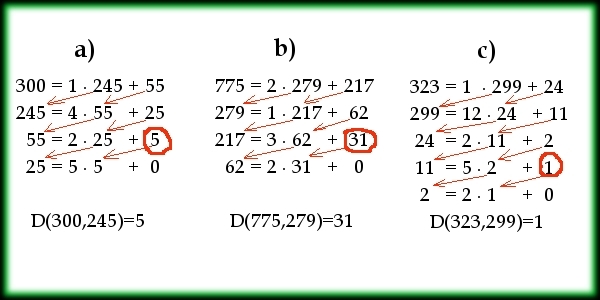
Evklidov algoritem:
Postopek nadaljujemo, dokler ne dobimo ostanka 0. |
1. primer
Z Evklidovim algoritmom določimo največji skupni delitelj števil 60 in 52. Dopolni. Pomagaš si lahko s prejšnjo animacijo.
Klikni sem za animacijo
| osnovni izrek o deljenju za števili 60 in 52 | 60 = 1 · 52 + |
| osnovni izrek o deljenju za števili 52 in 8 | 52 = · 8 + 4 |
| osnovni izrek o deljenju za števili 8 in 4 | 8 = · 4 + 0 |
Ko dobimo ostanek 0, končamo z Evklidovim algoritmom.
Zadnji od 0 različen ostanek je 4, zato je največji skupni delitelj števil 60 in 52 enak 4.
Pravilno Naprej
[--! animacija --]
1. 8
2. 6
3. 2
2. primer
Z Evklidovim algoritmom določimo največji skupni delitelj števil 88 in 121. Dopolni.
| osnovni izrek o deljenju za števili 121 in 88 | 121 = · 88 + |
| osnovni izrek o deljenju za števili 88 in 33 | 88 = · 33 + |
| osnovni izrek o deljenju za števili 33 in 22 | 33 = · 22 + |
| osnovni izrek o deljenju za števili 22 in 11 | 22 = · 11 + |
Ko dobimo ostanek 0, končamo z Evklidovim algoritmom.
Zadnji od 0 različen ostanek je , zato je največji skupni delitelj števil 121 in 88 enak .
Pravilno Naprej
1. 1
2. 33
3. 2
4. 22
5. 1
6. 11
7. 2
8. 0
9. 11
10. 11
3. primer
Z Evklidovim algoritmom določimo še največji skupni delitelj števil 208 in 124. Dopolni.
| osnovni izrek o deljenju za števili 208 in 124 | 208 = 1 · 124 + 84 |
| osnovni izrek o deljenju za števili in | = 1 · + 40 |
| osnovni izrek o deljenju za števili in | = 2 · + 4 |
| osnovni izrek o deljenju za števili in | = 10 · + 0 |
Zadnji od 0 različen ostanek je , zato je največji skupni delitelj števil 208 in 124 enak .
Pravilno Naprej
1. 124
2. 84
3. 124
4. 84
5. 84
6. 40
7. 84
8. 40
9. 40
10. 4
11. 40
12. 4
13. 4
14. 4
4. primer
Zdaj poskusimo z Evkildovim algoritmom določiti največji skupni delitelj števil 96 in 37. Pišimo le še račune. Dopolni.
| 96 | = 2 · 37 | + 22 |
| = · | + | |
| = · | + | |
| = · | + | |
| = · | + |
Največji skupni delitelj števil 96 in 37 je , torej sta števili 96 in 37 tuji.
Pravilno Naprej
1. 37
2. 1
3. 22
4. 15
5. 22
6. 1
7. 15
8. 7
9. 15
10. 2
11. 7
12. 1
13. 7
14. 7
15. 1
16. 0
17. 1
1. naloga
Z Evklidovim algoritmom poišči največje skupne delitelje naslednjih parov števil in poveži stolpca:
Pravilno Naprej
2. naloga
Pravilno Naprej
Največji skupni delitelj dobimo kot zadnji neničelni ostanek v Evklidovem algoritmu.
Kako pa dobimo najmanjši skupni večkratnik?
| Spomni se zveze a·b=D(a,b)·v(a,b). |
Določimo najprej največji skupni delitelj.
Evklidov algoritem:
| 1768 = 1 · 992 + 776 | ||
| 992 | = 1 · 776 | + 216 |
| 776 | = 3 · 216 | + 128 |
| 216 | = 1 · 128 | + 88 |
| 128 | = 1 · 88 | + 40 |
| 88 | = 2 · 40 | + 8 |
| 40 | = 5 · 8 | + 0 |
Največji skupni delitelj števil 992 in 1768 je enak 8.
3. naloga
Na dva načina določi največji skupni delitelj in najmanjši skupni večkratnik števil 4331 in 5183:
Največji skupni delitelj:
| 1. Praštevilski razcep 4331=61· 5183=71· | 2. Evklidov algoritem
|
Najmanjši skupni večkratnik:
4331·5183=·
Preveri Nauk te naloge
Pravilno Naprej
Morda se pa le splača poznati Evklidov algoritem...
1. 71
2. 73
3. 71
4. 4431
5. 71
6. 71
7. 71
8. 316163
Pravilno Naprej
krajšati ulomek = števec in imenovalec deliti z istim številom
kolikor se le da okrajšati ulomek = števec in imenovalec deliti z istim največjim možnim številom
Kako pa rečemo številu, ki deli dve števili in je največje možno? Izračunajmo ga.
Še več o Evklidovem algoritmu
Zdaj, ko obvladamo Evklidov algoritem, poskušajmo odgovoriti na naslednja vprašanja:
Ko imamo veliki števili in je težko uganiti delitelje ali narediti praštevilski razcep. Lahko pa ga uporabimo kar tako.
Ker osnovni izrek o deljenju vključuje le dve števili, lahko Evklidov algoritem uporabljamo le za dve števili.
Lahko pa si pomagamo takole:
Tako dobimo največji skupni delitelj treh števil.
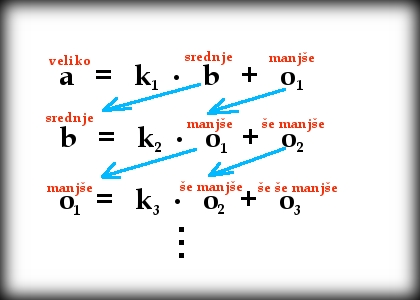
Pozorno opazuj sliko.
Prva vrstica:
In tako naprej...
Kaj se dogaja z ostanki? So vedno manjši. Tako moramo zagotovo priti do najmanjšega možnega ostanka 0. Takrat se Evklidov algoritem zaključi. Torej se Evklidov algoritem vedno mora končati po določenem številu vrstic.
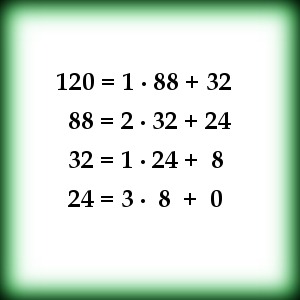
Skozi naslednje razmišljanje si pomagajmo z zgornjo sliko.
Od spodaj navzgor:
Torej sta obe začetni števili deljivi z zadnjim od 0 različnim ostankom (120 in 88 sta deljivi z 8).
Ugotovili smo: ZADNJI OD 0 RAZLIČEN OSTANEK DELI NAJVEČJI SKUPNI DELITELJ.
To pa še ne pomeni, da sta enaka. Nadaljujmo z razmišljanjem.
Od zgoraj navzdol
Ugotovili smo:NAJVEČJI SKUPNI DELITELJ DELI ZADNJI OD 0 RAZLIČEN OSTANEK.
Sklep:
| Števili, ki se vzajemno delita, sta enaki. Torej je zadnji od 0 različen ostanek ravno največji skupni delitelj. |
Preveri svoje znanje 1
Pravilno Naprej
Pravilno Naprej
Preveri svoje znanje 3
Pravilno Naprej
1. dodatna naloga
Pravilno Naprej
Pravilno Naprej
Števili sta tuji, ko je njun največji skupni delitelj enak 1. S pomočjo Evklidovega logaritma preveri, ali trditev drži.
3. dodatna naloga
Določi največji skupni delitelj in najmanjši skupni večkratnik naslednjih števil. Poveži stolpca.
Pravilno Naprej
4. dodatna naloga
Pravilno Naprej
5. dodatna naloga
Pravilno Končaj
Ker ploščic ne smemo rezati, mora stranica kvadrata hkrati deliti višino in širino bazena. Torej iščemo skupne delitelje dolžine in širine. Poiščimo najprej največji skupni delitelj. Da lahko to storimo, dolžino in širino spremenimo iz decimalnih števil v naravni.