Gostost realnih števil
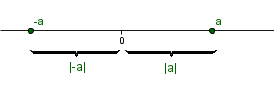
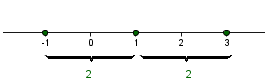
Pokazati želimo, da med dvema racionalnima številoma obstaja vsaj še eno racionalno število, zato želimo pokazati, da med številoma in leži aritmetična sredina teh dveh števil:
Dokaz:
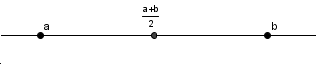
To res velja, saj je položaj na številski premici levo od . Zato med dvema racionalnima številoma obstaja vsaj še eno racionalno število:
|
Množica ulomkov je povsod gosta, saj lahko poiščemo razpolovišče tudi med in , in ,...
Uvedba realnih števil
Ali množica racionalnih števil popolnoma zapolni številsko premico? Ne.
|
Vendar število ne spada v množico naravnih, niti celih in ne racionalnih števil. Število je iracionalno število. Iracionalna števila so vsa števila, ki se ne dajo zapisati v obliki ulomka, teh pa je neskončno mnogo. Če bi poskusili zapisati iracionalna števila v decimalni obliki, bi dobili neskončno zaporedje neperiodičnih decimalk.
Množico realnih števil označimo z in jo dobimo z dodajanjem neskončnih neperiodičnih decimalnih števil k množici racionalnih števil.
Neko število je ulomek, če ga lahko zapišemo v obliki , kjer je celo, pa naravno število in . Zato moramo preveriti, če velja . Rešimo enačbo:
Ugotovili smo, da sta števili in sodi, zato si nista tuji. Za okrajšani ulomek pa velja, da sta si števili in tuji. Zato število ni racionalno.
Velja, da je . Podobno velja tudi in ... Postopek lahko nadaljujemo neskončno dolgo in zapišemo število v obliki neskončne decimalne številke, ki ni periodična. Zato ne moremo ugotoviti, koliko decimalk ima število, lahko jih le nekaj zapišemo.
Točke na številski premici
Na številski osi obstaja natanko ena točka, katere koordinata je . Velja tudi obratno, za izbrano točko T obstaja natanko eno realno število, ki je koordinata te točke.
Na sliki je prikazan postopek iskanja točke s koordinato .
|
Število se da zapisati v obliki neskončne decimalne številke.
Računske operacije v realnih številih
V množici realnih števil lahko izvajamo vse štiri osnovne operacije: seštevanje, odštevanje, množenje in deljenje, pri čemer je rezultat vedno realno število. Za operaciji množenja in seštevanja veljata zakona o zamenjavi in združevanju, velja pa tudi zakon o razčlenjevanju.
Če je in , velja:
| Nevtralni element za seštevanje je število 0. | |
| Nasprotno število k številu je . | |
| Odštevanje dveh realnih števil je enako prištevanju nasprotnega števila. | |
| Nevtralni element za množenje je število 1. | |
| Obratno število k številu je . | |
| , deljenje je enako množenju z obratnim številom. | |
| Ko potenciramo poljubno realno število z 0, je rezultat vedno 1. | |
| , | |
| , |
Urejenost realnih števil
Naj bosta . Potem velja:
kar pomeni, da leži desno od na številski premici in
kar pomeni, da ne leži levo od .
Vsa števila, ki na številski premici ležijo desno od koordinatnega izhodišča, so pozitivna realna števila: .
Vsa števila, ki na številski premici ležijo levo od koordinatnega izhodišča, so negativna realna števila: .
Množico realnih števil lahko zato zapišemo kot unijo treh paroma disjunktnih podmnožic: .
Intervali
Množico vseh realnih števil med in imenujemo interval, kjer sta števili in krajišči intervala. Ločimo več intervalov:
Zaprti interval s krajiščema in :
Odprti interval s krajiščema in :
Posebni primeri intervalov
Naj bo in znak za neskončno. Potem so posebni primeri intervalov poltraki:
Interval od do neskončno, vključno z :
Interval od do neskončno, brez :
Interval od - neskončno do , vključno z :
Interval od - neskončno do , brez : .
Če si ogledamo realna števila na številski premici, ugotovimo, da predstavljajo celotno številsko premico. Zato bi z intervalom lahko zapisali realna števila kot .
Zgled
Rešimo sistem neenačb in .
Rešitev
Vsako neenačbo rešimo posebej in nato poiščemo presek delnih rešitev:
x<3 |
Na številsko premico narišemo delni rešitivi:
| 
|
Skupna rešitev sistema neenačb pa je presek teh dveh rešitev:
|
Kvadratni koren
Obstaja natanko eno pozitivno realno število , da velja . Številu pravimo kvadratni koren števila in ga označimo z
Za je edino tako nenegativno realno število, da velja .
Primer:
Reševanje enačbe , kjer je a realno število:
Enačba nima realnih rešitev. | . | in |
Delno korenjenje in racionalizacija
Za računanje s koreni sta pomembni dve pravili:
sta nenegativni realni števili:
Delno korenimo v primeru, kadar se en faktor pod korenom lahko koreni, drugi pa ne:
Ker velja, da lahko enačbo kvadriramo na obeh straneh, njena vrednost pa se ne spremeni, lahko prav to storimo za dokaz pravila:
Pravilo res velja.
Veljavnost pravila lahko dokažemo na podoben način kot prej, s kvadriranjem:
Enakost res velja.
Z racionaliziranjem odpravimo koren iz imenovalca. To storimo tako, da imenovalec in števec pomnožimo oziroma razširimo.
Primeri
Absolutna vrednost
Razdaljo med točko in izhodiščem imenujemo absolutna vrednost. Razdalja nikoli ni negativna, zato tudi absolutna vrednost ni. Definicija:
|
Lastnosti absolutne vrednosti:
Za vsako realno število velja:
Absolutna vrednost števila je vedno pozitivna ali enaka 0: . Nič pa je enaka natanko takrat, ko je .
Primeri
Rešimo enačbo .
Rešitev
Grafično:
Rešimo enačbo .
Rešitev
Absolutni vrednosti dveh števil sta enaki, ko:
Približki in napake
Pri merjenju ali računanju z decimalnimi številkami se hitro lahko zmotimo in rezultat ni natančen. Prav tako ni vedno natančno žepno računalo in ne merilne naprave. Glede na vrsto napake ločimo:
1. Absolutna napaka Naj bo prava vrednost, natančno število in približna vrednost, približek. Potem je
tega približka.
Primer: Izmerili smo dolžino učilnice, ki je 8,11 m, dovoljena absolutna napaka pa je 1 cm. V katerih mejah se lahko giba dolžina učilnice?
Zaokroževanje
Oglejmo si število in ga zapišimo na 1, 2, 3, 4, 5, 6 decimalk.
| na eno mesto | 2 |
| na eno decimalko | 1,7 |
| na dve decimalki | 1,73 |
| na tri decimalke | 1,732 |
| na štiri decimalke | 1,7321 |
| na pet decimalk | 1,73205 |
| na šest decimalk | 1,732051 |
Pravilo zaokroževanja:
Če je prva odrezana števka 0,1,2,3 ali 4, potem pustimo preostale števke nespremenjene.
Če je prva odrezana števka 5,6,7,8 ali 9, potem zadnjo od preostalih števk povečamo za 1.
Tista števila, ki v decimalnem številu kaj pomenijo, so vse števke razen ničel na začetku. Na primer, pri številu 2,13 so pomembne števke 2, 1 in 3. Pri številu 0,0147 so pomembne števke 1, 4 in 7, pri številu -2,180 pa števke 2, 1, 8 in 0. Po navadi rečemo, da ima prvo število tri mesta, drugo tri mesta in tretje štiri mesta.
Na desetine: 2,9. Ker je števka, ki sledi desetinam, 9, moramo števko 8 povečati za 1, zato je zaokrožena vrednost 2,9.
Na stotine: 2,90. Ker je števka, ki sledi desetinam, 9, moramo števko 9 povečati za 1. Zato pa moramo povečati tudi prejšnjo števko, da je zaokroževanje pravilno. Zaokrožena vrednost je potem 2,90.
Napaka vsote in razlike
Imamo dve števili, in , ki sta točni vrednosti.
Njuna vsota pa je .
Če zaokrožimo na dve mesti, dobimo približek , približek za pa je .
Njuna vsota je .
Opazimo, da je zadnja števka v vsoti približkov napačna. Pri računanju pa se te napake še večajo.
Imamo dve števili, in .
Njuna razlika je
Če zaokrožimo na tri mesta, dobimo približek , približek za pa je
Njuna razlika je .
Napaka je velika.
Ko želimo rezultat zapisati na 1 decimalko natančno, vmesne rezultate oziroma števila zaokrožujemo najmanj na 2 decimalki in šele končni rezultat zaokrožimo.
Če vzamemo števili in ter ju zmnožimo med sabo, dobimo produkt . Če pa števili zaokrožimo, dobimo in , zmnožek pa . Spet pride do napake zaradi zaokroževanja. Zato se množi oziroma deli približke tako, da se končni rezultat zaokroži na mest, kjer je število mest, ki jih imajo podatki.
